基于事件驱动的随机多智能体系统的一致性

马文周, 柏晓明

(合肥工业大学 数学学院,安徽 合肥 230601)

0 引 言

多智能体系统通常是指由大量具有通信连接的智能体所组成的系统。借助智能体间的信息交换,系统在整体上可以呈现出单一智能体所不具备的行为,这种系统在生物、工程和社会等领域广泛存在。多智能体系统的一个基本问题就是趋同问题;趋同问题就是设计合适的分布式协议,最终使多智能体系统的每个智能体的状态达到一致。文献[1-8]中的控制协议大都建立在多智能体之间的连续通讯的基础上,这将消耗大量的通讯资源。为了达到节省通讯资源的目的,事件驱动方法被引入了网络控制系统中,即只有在满足事件驱动触发条件时,多智能体之间才互相通讯。

基于事件驱动的控制是现在网络控制系统中的一个热门话题[9-18]。文献[9]证明了经典事件驱动策略控制下,控制系统无芝诺行为发生,可有效节省通讯资源。文献[10-16]分别探讨了在无噪声假设下不同类型有效的事件驱动触发方案以及事件驱动控制协议，其中文献[11]提出了一种区别于以往的集中事件触发方案,能更有效地降低智能体间通讯频率,且避免了芝诺行为的发生。文献[17-18]探讨了在有乘性系统噪声存在下的带事件驱动的多智能体系统一致性问题,并且分别给出了在有噪声假设下的有效的事件触发方案以及事件驱动控制协议，其中文献[17]通过随机变量期望的上下界函数以及引入的一个内部动态变量在保证系统的均方一致性的同时避免了芝诺行为的发生;文献[18]通过随机变量的期望以及引入一个内部变量的方法保证系统的均方一致性与无芝诺行为发生。

本文参考文献[17-18]方法,采用文献[11]的事件驱动控制协议证明了在该事件驱动控制下带领导者的线性随机多智能体系统可以达到均方一致,且无芝诺行为发生;最后通过数值模拟,验证了理论分析的正确性。

本文中‖·‖表示向量2范数与矩阵的2诱导范数。(Ω,F,{Ft}t≥0,P)为完备概率空间,其中，Ω为样本空间;F为σ-域;{Ft}t≥0为滤子;P为概率测度。

1 问题描述

1.1 预备知识

A=[aij]∈RN×N为图G的邻接矩阵,当且仅当(i,j)∈E时,aij=1,aii=0,其余aij=0。定义对角矩阵D=diag{d1,d2,…,dN},当且仅当顶点i可以从领导者处获取信息时,di=1,其余di=0。定义拉普拉斯矩阵为:

记H=L+D。

考虑带N个跟随者的多智能体趋同控制系统:

(1)

其中:i=1,2,…,N;xi(t)∈Rn表示多智能体状态；x0(t)表示领导者状态；ui(t)∈Rn表示智能体i的控制输入；A∈Rn×n、B∈Rn×m、C∈Rn×n都为多常数矩阵；wi(t)表示定义在概率空间(Ω,F,{Ft}t≥0,P)上的一维布朗运动。

1.2 集中事件驱动控制

定义测量误差为:

(2)

本文使用事件驱动控制协议为:

(3)

其中,K=BTP,P为满足假设条件的正定矩阵。跟随者i的控制输入由上一次事件驱动时跟随者与领导者的状态以及时间间隔t-tk计算得来。

用δi(t)=xi(t)-x0(t)表示跟随者i逼近领导者状态的程度。

dδ(t)=(IN×N⊗A)δ(t)-(H⊗BK)(δ(t)+

e(t))dt+(IN×N⊗C)δ(t)dw(t)

(4)

事件触发时间序列{tk}定义如下:

tk+1=inf{t>tk|E‖(IN⊗N⊗K)e(t)‖2-

βE(‖H⊗K)δ(t)‖2)-λ(t)>0}

(5)

其中

E‖(IN×N⊗K)e(t)‖2)-σλ(t)

(6)

且β,σ>0;λN>0为矩阵H的最大特征值。领导者的所有跟随者共享同一个事件触发时间序列。

假设1 代数黎卡提不等式

CTPC+I<0

(7)

有正定解。其中,λ1、λN分别为矩阵H的最小、最大特征值。

本文使用文献[11]中事件驱动控制策略,参考文献[17-18],在其事件触发机制中引入随机变量的期望以及一个内部动态变量,使该事件驱动控制策略在有乘性噪声的环境中依旧能有效地避免芝诺行为，且文章事件触发机制中考虑了增益矩阵K,这与文献[17-18]均不相同。

2 引理及定理

引理1[19]当且仅当图G是连通图时,由图G决定的矩阵H正定。

显然,若图G中存在m个连通分量,且每一个连通分量都可以从领导者处获取信息,各连通分量间互相不通讯。单独每个连通分量与领导者决定的矩阵Hi正定,由图G决定的矩阵:

也为正定矩阵。

(8)

若μ2(A)<0,则

μ2(A)≥-(‖A-1‖)-1≥-‖A‖

(9)

引理4[22](Gronwall不等式) 设r(t)、h(t)、y(t)是定义在[a,b]上的连续函数,r(t)≥0,h(t)≥0,且对∀t∈[a,b],都有：

则

若h(t)为常数h,则

引理5系统(1)中,对于∀t∈[tk,tk+1),E(‖(IN⊗N⊗K)e(t)‖2)与E(‖(H⊗K)δ(t)‖2)分别存在如下上界函数、下界函数:

Γ1(δ(tk),t-tk)≥E(‖(IN×N⊗K)e(t)‖2)

(10)

Γ2(δ(tk),t-tk)≤E(‖(H⊗K)δ(t)‖2)

(11)

其中

Γ1(δ(tk),t-tk)=

(exp{2μ2(A)(t-tk)}-exp{a(t-tk)});

Γ2(δ(tk),t-tk)=

(exp{-b(t-tk)}-exp{2μ2(A)(t-tk)})+

E‖H⊗Kδ(tk)‖2exp{-b(t-tk)};

λmin(KTK)为矩阵KTK的最小非0特征值。

证明设

Γ(t)=‖(IN×N⊗K)e(t)‖2,t∈[tk,tk+1)。

由Dynkin公式得:

E(‖(IN×N⊗K)e(t+ε)‖2|Ft)=

‖(IN×N⊗K)e(t)‖2+

eT(s)(IN×N⊗CTKTKC)e(s))ds|Ft]

由ε的任意性以及富比尼定理可知:

D+EΓ(t)=2EeT(t)(IN×N⊗KTKA)e(t)+

EeT(t)(IN×N⊗CTKTKC)e(t)≤

‖KKT‖)E‖(IN×N⊗K)e(t)‖2+

由(8)式得:

E‖(H⊗K)δ(tk)‖2exp{2μ2(A)(t-tk)},

其中,λmin(HH⊗KTK)为矩阵HH⊗KTK的最小非0特征值。

由(8)式、(9)式易知a-2μ2(A)>0。由引理3及

Γ(tk)=E(‖(IN⊗N⊗K)e(tk)‖2)=0,

即得(10)式。

同理,可设

Φ(t)=-E‖(H⊗K)δ(t)‖2,

得

D+(EΦ(t))≤

E‖(H⊗K)δ(tk)‖2exp{2μ2(A)(t-tk)}。

由比较法则以及Φ(tk)=-E‖(H⊗K)δ(tk)‖2即得(11)式。

证明设

显然有S1>0,S2>0。

等式Γ1(δ(tk),T)=βΓ2(δ(tk),T)两边同时除以exp{2μ2(A)T},则有:

S1(exp{(a-2μ2(A))T}-1)=

βS2(exp{(-b-2μ2(A))T}-1)+

βexp{(-b-2μ2(A))T}。

设

f(T)=S1(exp{(a-2μ2(A))T}-1)-

βS2(exp{(-b-2μ2(A))T}-1)-

βexp{(-b-2μ2(A))T}

(12)

而

f(0)=-1<0

(13)

(14)

f′(T)=(a-2μ2(A))S1exp{(a-2μ2(A))T}+

(b+2μ2(A))βS2exp{(-b-2μ2(A))T}+

(b+2μ2(A))βexp{(-b-2μ2(A))T}>0

(15)

故f(T)在T∈(0,+∞)上单调递增。由(13)式、(14)式可知,方程f(T)=0存在唯一大于0的解T*。

当a≥b,μ2(A)>0时,设

g(T)=S1(exp((a+2μ2(A))T)-1)-

βS2(exp((-a-2μ2(A))T)-1)-

βexp((-a-2μ2(A))T),

显然g(T)也是单调递增函数,且f(T)≤g(T)。

同上易证,存在T*,使得0=g(T*)≥f(T*)。

记y=exp{(a+2μ2(A))T},令g(T)=0,即

S1y2+(βS2-S1)y-βS2-β=0。

解上述方程,舍去负值,解得:

同理,

因为S3>0且y*>1,所以有T*>0。

易知,T*由仅与系统参数矩阵、增益矩阵、由拓扑确定的矩阵H、常数β有关。

证明设

(16)

dV(t)=LV(t)dt+

ej(t)-ei(t)]-di(δi(t)+ei(t))}+

δT(t)(IN×N⊗(ATP+PA+CTPC)-

H⊗2PBBTP)δ(t)-

δT(t)(H⊗2PBTBP)e(t)≤

δT(t)(IN×N⊗(ATP+PA+CTPC)-

H⊗2PBBTP)δ(t)+

δT(t)(H⊗PBBTP)δ(t)+

eT(t)(H⊗PBBTP)e(t)≤

δT(t)(IN×N⊗(ATP+PA+CTPC)-

H⊗PBBTP))δ(t)+

λNeT(t)(IN×N⊗PBBTP)e(t)

(17)

由(5)式、(6)式与引理1易知λ(t)≥0。

设S(t)=V(t)+λ(t),由(6)式、(7)式、(17)式可得:

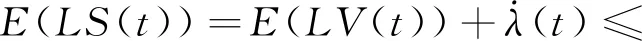
E(δT(t)(IN×N⊗(ATP+PA+CTPC)-

H⊗PBBTP))δ(t)+

βλNδT(t)(HH⊗PBBTP)δ(t)-σλ(t)≤

E(δT(t)(IN×N⊗(ATP+PA+CTPC)-

H⊗PBBTP))δ(t)+

E(LS(t))≤E(δT(t)|IN×N⊗

CTPC)δ(t))-σλ(t)≤

-E(δT(t)δ(t))-σλ(t)≤

-E(δT(t)δ(t))

(18)

而

对∀t∈[t0,+∞),有

(19)

由引理4可得:

(20)

显然

且带领导者的系统可达均方一致。

由引理6及(5)式、(6)式、(10)式、(11)式可知,对∀t∈[tk,+∞),若

E(‖(IN×N⊗K)e(t)‖2)-

βE(‖(H⊗K)δ(t)‖2)-λ(t)=0

存在解t1,则有t1-tk≥T*。

假设在上述事件驱动下,存在k,使得tk+1-tk=τk

由(15)式可知,f(T)为单调递增函数且f(T*)=0,因此

Γ1(δ(tk),τk)-βΓ2(δ(tk),τk)<0。

若事件驱动在tk+1时触发,λ(tk+1)>0,则

0=E(‖(IN×N⊗K)e(tk+1)‖2)-

βE(‖(H⊗K)δ(tk+1)‖2)-

λ(tk+1)≤Γ1(δ(tk),τk)-

βΓ2(δ(tk),τk)-λ(tk+1) ≤

Γ1(δ(tk),τk)-βΓ2(δ(tk),τk)<0。

矛盾!

因此在上述事件驱动控制下,任意2个时间驱动触发时刻间的时间间隔不会小于T*,故系统无芝诺行为发生。

3 数值模拟

考虑带领导者的多智能体系统如下:

考虑有1个领导者7个跟随者的有向图,将领导者的所有跟随者分属于2个联通子图,如图1所示。

每个联通子图可自领导者处获取信息。

图1 有领导者及2个联通子图的有向图

取β=0.03,求得满足定理1要求的增益矩阵为:

取σ=1,做仿真模拟，如图2、图3所示。可见系统趋同效果良好。

事件驱动触发时刻图如图4所示。在该事件驱动下,系统多智能体间通讯次数为545次,较之连续通讯600 00次,可节省大量通讯资源,且最小事件间隔为0.002 8,无芝诺行为发生,见表1所列。

图2 智能体状态趋同效果图

图4 事件触发时刻图

表1 事件触发次数与时间间隔

4 结 论

本文基于事件驱动方法对有乘性噪声的线性对多智能体系统的均方一致性进行了研究,利用随机分析和微分方程稳定性理论方法证明了带领导者的线性随机多智能体系统在该控制策略下可达均方一致,并证明了该事件触发方案能够避免芝诺行为的发生。最后通过仿真,验证了该事件触发方案可有效减少多智能体间通讯次数,避免芝诺行为。