灰色幂模型在基坑变形监测中的应用

张 进 彭 磊 尹亚东

(中国电建集团河北省电力勘测设计研究院有限公司, 河北 石家庄 050015)

0 引言

近年来,我国经济飞速发展,基础建设速度的加快和施工难度的逐渐增大,对工程安全性的要求也是越来越高,如在地质环境脆弱的地区建设高层建筑物,在地下水密集的地带开挖隧道,在建筑物密集的城市中心建设地铁轨道交通使得建筑物产生沉降。在工程运营的整个过程中需要及时预测和准确预报建筑物的形变量和状态,这不仅对整个工程的施工和管理至关重要,也关系到人民的生命财产安全[1]。

灰色模型可以利用小样本量和少信息量对不确定的数据来进行预测和拟合,并且由于灰色模型具有简便和可操作性强的特点,被广泛应用在多领域的预测和分析中[2]。传统GM(1,1)模型对于具有非线性特征趋势的数据没有较好的预测效果[3]。灰色幂模型NGBM(1,1)是传统GM(1,1)模型的一种重要改进模型,灰色幂模型是一种可以拟合和预测具有非线性特征数据序列的模型,它可以通过改变自身的参数来适应不同变化趋势的数据类型[4]。由于灰色幂模型是GM(1,1)模型的拓展形式,所以它具有灰色模型的性质,可以用“小样本”和“贫信息”的数据来进行预测,此外还在一定程度上扩大了灰色模型的适用范围和精度。本文将灰色幂模型应用在基坑监测预报中,并对应用过程进行分析,与传统模型进行对比。

1 灰色模型的建立

首先,是对原始数据序列进行累加,从第二项开始累加,新的序列的每个值是原始序列的第一个值到新的序列所对应的值的累加所得,假设非负的原始数据序列为:

X(0)=(x(0)(1),x(0)(2),…,x(0)(n))

那么X(0)的一次累加生成序列为:

X(1)=(x(1)(1),x(1)(2),…,x(1)(n))

然后,根据一次累加序列求出背景值序列,背景值生成是在求解灰色模型时,以每相邻的两个一次累加序列值取平均值或取两个一次累加值中间的某一值,假设Z(1)为X(1)紧邻均值生成序列:Z(1)=(z(1)(2),z(1)(3),…,z(1)(n)),其中,

z(k)=px(1)(k)+(1-p)x(1)(k-1),
k=2,3,…,n

(1)

p取0到1之间的任意一值,一般情况下取p=0.5,其中Z(1)称为背景值。

利用累加序列和背景值序列构建如下方程:

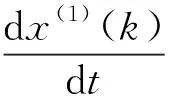
(2)

称式(2)为GM(1,1)模型。

2 灰色幂模型

在已经得到的灰色GM(1,1)模型作用量b后乘背景值的γ次方,即(z(1)(k))γ,其中γ≠1,得到具有非线性特征的灰色幂模型NGBM(1,1):

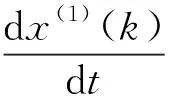
(3)

式中,γ为幂指数,可以根据不同的变形监测数据来调整幂指数γ,使预测的精度达到最优。其中,GM(1,1)模型为NGBM(1,1)模型在γ=0时的形式。

灰色幂模型NGBM(1,1)的白化方程的解为:

(4)

它的解变为:

(5)

设X(0),X(1),Z(1)如上所述,建立矩阵:

将式(5)化简成下式:

(6)

(7)

最后,用累加生成的序列和均值序列进行计算后,需要对求解灰色模型得到的新序列进行处理,得到其拟合和预测的数据序列,对累加生成的序列进行逆运算,即累减生成:

(8)

幂指数γ可以根据式(4)进行迭代求解,除此之外,用优化算法也可以求解幂指数值,优化算法中比较常见的有:PSO算法、蚁群算法和遗传算法等,利用这些算法对求解过程优化,以此得到最佳幂指数值。

3 精度评定

对灰色幂模型的预测和拟合的精度检验应该使用残差检验、后验差检验这两种方法。残差检验是对每个拟合值和预测值与原始值求差得出结果,一般用其平均值来评价整体的拟合预测效果;后验差检验是根据残差概率统计方面的特性来对预测和拟合的结果进行评价。

3.1 残差检验

假设原始的数据序列为:

x(0)=(x(0)(1),x(0)(2),…x(0)(n))

用灰色幂模型进行计算得到的拟合数据序列为:

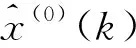
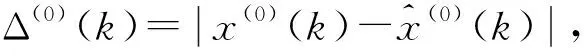
(9)

每个拟合值的相对误差为:

(10)

用其相对误差的平均值来评价整体的精度:

(11)

3.2 后验差检验

假设原始的数据序列为:

x(0)=(x(0)(1),x(0)(2),…,x(0)(n))

它与真实值的残差序列为:

Δ(0)(k),k=1,2,…,n

然后分别计算原始数据序列的平均值和残差序列的平均值可以分别得到:

(12)

(13)

再根据原始数据序列的平均值计算它的方差可以得到:

(14)

并计算残差值的方差:

(15)

计算两者之间的比值,得到式(16),称其为后验差:

(16)

根据残差值和其方差分布规律,计算得到其小误差概率:

(17)

根据C值和P值的大小对模型的拟合精度进行评定:

当P>0.95,C<0.35时,拟合的精度为一级(优);

当P>0.8,C<0.5时,拟合的精度为二级(合格);

当P>0.7,C<0.65时,拟合的精度为三级(勉强合格);

当P≤0.7,C≥0.65时,模型拟合的精度为四级(不合格)。

4 工程实例

某工程基坑挖深至垫层底为-9.6 m,基坑周长约600 m,挖深约4.1～7.6 m。在变形监测中,采用独立的高程系,按二等水准测量的方法,对监测点进行测量,仪器自动记录观测数据;观测结束后把观测数据输入至计算机作后处理;使用清华山维高程网严密平差程序,在计算机上计算基准点高程值。其中环线闭合差0.4 mm,达到《建筑变形测量规范》(JGJ8-2016)级别二级精度要求。为了验证灰色幂模型比灰色模型有更高的拟合和预测精度,本文取此工程坡顶沉降监测WY2号点分别用灰色模型和灰色幂模型进行拟合和预测。以基坑坡顶沉降点WY2号点为例,它的沉降数据序列为:

X(0)=[0.22 0.57 0.78 0.89 1.24 1.46 1.63 1.70 1.78 1.99 2.08 2.23 2.38 2.45 2.56 2.62];

不妨取前11项数据,来预测后5项数据。根据已有数据进行求解,用灰色幂模型来对其进行拟合预测,第一步是要根据变形监测数据来求取最佳的幂指数,本文根据前11项数据用等步长试探法求取灰色幂模型的最佳幂指数,以0.01为步长从0到2逐个试探,得到幂指数取值和相对误差的关系,当相对误差最小时的幂指数值,即待求幂指数值,相对误差与幂指数取值的关系如图1所示。

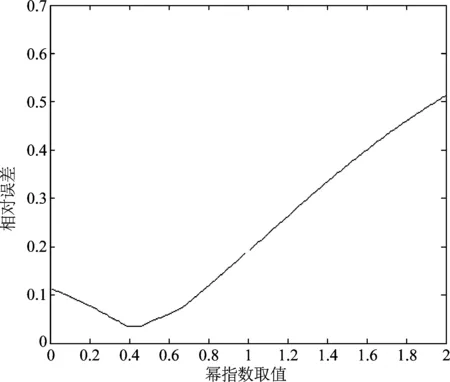
图1 相对误差与幂指数取值关系

当幂指数γ=0时,灰色幂模型变为灰色模型。从图1中可以看出,灰色GM(1,1)模型(幂指数为零时)并非为误差最小的结果。当相对误差最小时,幂指数的取值为γ=0.42。

因此,可以得到灰色模型GM(1,1)模型的白化方程参数为:

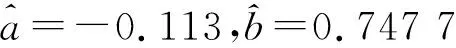
得到灰色幂模型NGBM(1,1),模型白化方程参数为:

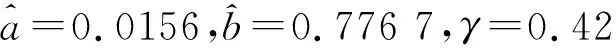
精度检验的结果用残差C和后验差P来对比。其中,残差C越小,后验差P越大说明精度越好。本文将两种方法拟合和预测的结果绘制成表格和线状图,结果如表1所示。

表1 灰色模型和灰色幂模型拟合预测对比(基坑监测点) 单位:mm

将表1中两种模型拟合预测的结果绘制成线状图如图2所示。

图2 灰色幂模型与灰色模型拟合预测对比(基坑监测点)

根据结果可以看出,灰色幂模型NGBM(1,1)拟合预测精度比灰色模型高,在变形监测中对非线性特征的数据预测精度比灰色模型有所提高,在基坑监测中的应用比较可靠。

5 结束语

本文在传统灰色模型GM(1,1)的基础上,总结了灰色幂模型NGBM(1,1),并对灰色幂模型的参数求解过程进行了说明,结合基坑监测的特点,将其应用在基坑监测预报分析中。通过实验可以看出,灰色幂模型相较灰色模型在预测精度上有了较大的进步。自从灰色系统理论提出以来,灰色模型得到了较大的发展,多种改进和组合模型被提出,提高了数据拟合和预测的精度,扩大了灰色模型的适用范围。灰色幂模型这一理论的出现为灰色系统理论又增添了新的内容,丰富了灰色体系统理论体系,灰色幂模型的改进与发展对提高变形监测预报分析的精度有极大的帮助。