一种洋葱地址快速生成算法Shallot++

魏海州，杨 云，李凌燕

(扬州大学 信息工程学院，江苏 扬州 225127)

1 引 言

匿名通信正在快速增长，越来越多的互联网用户使用匿名系统(如Tor或I2P[1])来隐藏其在线活动.从安全角度出发，对这些网络的研究也越来越多.

Tor网络是一个“覆盖网络”[2,3]，其设计理念是允许用户匿名访问外部Internet服务和提供隐藏服务，因此，Tor提供了两种操作方式：Web服务方式和洋葱服务方式.Web服务方式是用户通过Tor网络可以匿名访问Internet Web，网站无法知道用户IP地址.洋葱服务方式是用户通过Tor网络的洋葱浏览器，访问Tor网络提供的洋葱服务，用户无法得知服务器IP地址.

Internet DNS是基于IP地址的、提供本地化域名解析服务协议，它是Internet最重要的基础设施，而Tor网络不使用IP地址，Tor DNS是基于内容的(洋葱地址)、提供远程域名解析服务协议，主要协议有Hidden service协议和Onion routing协议等[4].

洋葱服务最初被称为“隐藏服务”，隐藏服务本来是为合法内容提供商提供匿名性，它包括私人内部网(如公司、政府机构或大学等内部网络)、学术论文数据库、商业数据库或内部论坛才能搜索的网站内容，需要账号密码或访问权限才能访问.但目前一些非法内容的论坛/聊天平台、黑市等提供商，利用为内容服务商提供的的匿名性提供洋葱服务.洋葱服务在2015年重新命名，以反映他们提供更多的服务事实而不只是服务的“隐藏”，更重要的是，它们提供端到端的安全性和自我认证的主要名称.洋葱服务是基于TCP的网络服务，只能通过Tor网络访问并提供相互联系匿名：Tor客户端对服务器是匿名的，并且服务器对客户端也是匿名的.

为了保护提供洋葱服务的服务器端在线隐私、防止网站被假冒或攻击、逃避监管等，服务器端必须匿名，隐藏真实网络地址与地理位置信息，因此，提供洋葱服务的Tor网站采用公钥字符串，并且在后缀添加.onion构成自己的域名.由于采用公钥的域名不友好、难以记忆，使用不方便，限制了洋葱服务的推广应用.

为了使域名具有一定可读性、便于记忆，在不降低安全性的前提下，设计具有指定字符的.onion域名，即：生成自定义.onion地址.国外许多学者进行了大量研究，开发了匿名域名生成工具，发布了自定义.onion域名，其中最经典的是2010年3月发布的 katmagic的Shallot域名生成工具、2014年10月Facebook发布了著名的公钥域名洋葱地址(1)facebookcorewwwi.onion、2019年5月7日，美国中央情报局CIA在Twitter上公布其暗网链接(2)ciadotgov4sjwlzihbbgxnqg3xiyrg7so2r2o3lt5wz5ypk4sxyjstad.onion等.事实上，生成具有指定字符串的公钥域名是非常困难的，尤其是随着指定字符串个数的增加，计算复杂度呈指数级增长，属于NP完全问题.值得注意的是，Facebook或CIA的洋葱地址生成算法都是基于Shallot的改进.

通过分析比较，基于Shallot算法，作者设计的Shallot++算法，可以减少计算的复杂度，对于指定字符串，Shallot++算法比Shallot算法可以更快地生成符合要求的域名.

2 相关工作

2.1 .onion TLD格式

Tor的洋葱服务以其特殊域名而闻名，.onion是一个特殊用途的顶级域名后缀，可依据.onion TLD中的地址(一般称为“洋葱地址”)通过Tor网络访问匿名洋葱服务.洋葱地址不是实际的DNS名称，并且.onion TLD不在Internet DNS根目录中，Internet DNS上无法解析它，是通过Tor DNS进行解析.

.onion TLD中的洋葱地址通常是不透明的、非助记符，包括所有字母和数字2-7，它们不区分大小写.洋葱服务地址是从服务器的公共RSA密钥算法生成的，地址是服务器RSA密钥的、SHA-1哈希的前16个字节的base32编码.

在Tor中依据生成洋葱地址的私钥对用户进行身份验证，再使用公钥哈希的洋葱地址作为联系洋葱服务的URL.

2.2 研究进展

一般的域名名称应具有全球性、安全性和令人难忘的特征，但由于匿名网络的洋葱服务要“隐藏”，所以它的名称不具有“令人难忘”的特征，因此，操作不方便，影响其服务的推广应用.在保证安全的前提下，为了其具有“令人难忘”的特征，即：名称中包含熟知的字符串或指定字符串，Tor工程师和许多学者进行了大量的研究，开发了几个洋葱地址生成工具，取得了一些成果.

2010年3月发布的katmagic的Shallot，密码规格为RSA1024和SHA1、操作系统面向OpenBSD或Linux、采用C语言编译器的单模式哈希域名生成器，洋葱地址长度为16个字符.由于RSA1024密钥和SHA1散列的计算都是在CPU完成的，所以速度较慢.

由于Shallot的密码规格仅支持1024b的RSA，密码强度不够；操作系统不支持Windows，影响了推广使用；基于CPU计算RSA和SHA处理速度慢.2012年10月发布的lachesis的Scallion，支持多种RSA密钥长度(1024b、2048b和4096b)和SHA1、操作系统面向Linux或Windows7、采用C#语言编译器的多模式哈希域名生成器，洋葱地址长度为16个字符.由于RSA(1024、2048、4096)密钥和SHA1散列的计算都是在GPU上完成的，处理速度快.

使用Scallion需要强大的计算资源，一般用户无法达到此要求，因此，可以考虑部分使用GPU，另一方面RSA的强度是建立在密钥长度基础上的，而椭圆曲线ECC[5]的强度是不依赖于密钥长度的.2013年2月发布的Unperson Hiro的Eschalot，密码规格支持ECC160和SHA1、操作系统面向OpenBSD或Linux、采用C语言编译器的单模式哈希域名生成器，洋葱地址长度为16个字符.ECC160密钥计算是在CPU上完成，而SHA1散列是在GPU完成的，处理速度没有Scallion快.

随着计算机性能的提高，利用云和GPU计算破解散列函数SHA1成为可能，存在安全隐患[6].2017年10月发布的cathugger的mkp224o，密码规格支持ECC160和SHA3、操作系统面向OpenBSD或Linux、采用C语言编译器的单模式哈希域名生成器，洋葱地址长度为56个字符.ECC160密钥计算是基于CPU，而SHA3散列计算是基于GPU的，速度较快.

遵循传统，作者保持匿名，katmagic、lachesis、Unperson Hiro和cathugger都是作者的假名.事实上Scallion、Eschalot和mkp224o都是基于Shallot的，只是算法实现不同.域名生成算法实现的难点在于如何合理地利用计算资源和存储资源，提高处理速度，获得安全等级更高、具有“令人难忘”特征的域名或地址.

3 洋葱地址快速生成算法Shallot++

Shallot算法的最大缺点是将奇数作为RSA公钥中的加密指数e，而模数n的欧拉函数φ(n)为偶数，为了满足RSA算法的条件，要求e与φ(n)互素，因此会浪费大量的时间去计算非互素的情况.同时，Shallot算法中加密指数e限制为小于1099511627775，经验上e选取为16位的素数，这样既可以有效的防止攻击，又可以获得较快的加、解密速度.针对这个问题，Shallot++对公钥中的加密指数e的选取进行优化，并且重新设计了对公钥进行哈希的方式，可以显著地减少计算量，加快处理速度，提高域名地址的安全性.

3.1 有效测试率

为了能够更好地描述算法性能，引入一个概念：有效测试率.想要生成指定的.onion域名，需要不断的变换公钥，然后对公钥进行哈希运算.在不断的碰撞测试中，大量的哈希运算是算法性能的瓶颈.因此，进行有效的测试会大大提高算法的性能.

基于RSA的.onion域名生成，由模数n和加密指数e组成公钥(n,e)，其中n=p×q，p与q为大素数.设Max为需要测试的总次数，即需要进行哈希运算的次数，取e不大于Max，φ(n)=(p-1)×(q-1)，令集合K为所有满足gcd(e,φ(n))=1的e的取值，如式(1)所示.

K={e|gcd(e,φ(n))=1,e≤Max}

(1)

取集合K内元素的个数为m，则有效测试率P可以表示为式(2).

(2)

定义每次进行哈希运算的速率为V，则无效的计算时间T表示为式(3).

T=(1-P)×V

(3)

式(3)中，有效测试率P的值越大，无效的计算时间T就越少.假设在测试时，满足指定域名的公钥(n,e)中加密指数e的取值不在集合K内，虽然生成的域名符合预期值，但是不满足RSA算法.因此，有效测试率P的增加，算法的效率也会随之提高.

3.2 Shallot算法

对Shallot算法基本步骤进行概述，并对算法中存在问题进行分析.

3.2.1 算法基本步骤

步骤1.随机选取两个大素数p(512bit)和q(512bit)，令n=p×q；

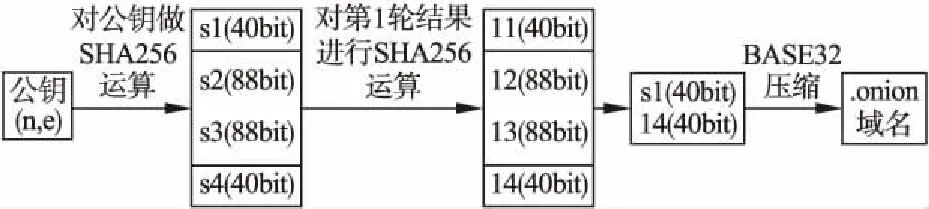
步骤3.选取整数e=65537作为加密指数，满足条件1

步骤4.判断e是否小于m(算法里设置m最大值为0xFFFFFFFFFF)，是则转步聚5，否则转步骤1；

步骤5.对公钥(n,e)使用SHA-1，产生160bit哈希值.取哈希值前半段(80bit)；

步骤6.对哈希值使用Base32进行转码，得到16个字符的域名.检查域名是否符合预期，并且判断gcd(e,φ(n))是否为1，即e与n的欧拉函数φ(n)的最大公约数是否为1.是则转步骤8，否则转步骤7；

步骤7.令e=e+2，转步骤4；

步骤8.求解解密指数d，即d=invert(e,φ(n))，满足条件e×d=1modφ(n)，算法结束；

在Shallot算法中，步骤1-步骤4是计算RSA1024，获得公钥(n,e)；步骤5计算SHA-1，获得160bit哈希值；步骤6分为两个部分：第1部分对获得的160bit哈希值使用Base32进行转码，得到16个字符的域名；第2部分对得到的16个字符域名进行符合性检查：是否包含指定字符串.

3.2.2 Shallot算法存在问题

从有效测试率和安全性两个方面分析.

1.有效测试率.在Shallot中，e的取值为小于Max的所有奇数.为了验证其算法有效测试率P的值，首先随机生成RSA对象，取e不大于4294967295(十六进制数为FFFFFFFF)，计算出n的欧拉函数φ(n)，即φ(n)=(p-1)×(q-1).根据式(1)、式(2)，通过计算得到集合K内的元素个数m为1711315240，测试总次数Max为2147483646，有效测试率P为79.68%，在Shallot算法中，会有20.32%的无效碰撞测试，这不仅增加了CPU的负担，同时也降低了产生指定域名的命中率，会产生大量无效的计算时间，导致算法效率不高.并且随着公钥中加密指数e的不断加大，在判断gcd(e,φ(n))是否为1时需要的计算量会增加.因此，产生指定域名的字符个数所需要时间会呈指数级增长；

2.安全性.主要有3个方面：

1)在Shallot算法中，选取随机大素数p与q时，均为512bit，故生成的模数n为1024bit，已经不能满足现如今密码学安全性的要求[7].RSA1024计算公钥，2009年12月12日，编号为RSA-768(768 bits,232 digits)数被成功分解；

2)SHA-1计算散列，2017年2月23日，Cryptology Group at Centrum Wiskunde & Informatica(CWI)和Google的研究人员发表了“SHATTERED”论文，宣布发现了2个不同的PDF文档，但是它们的SHA-1校验值是一样的，即：SHA-1碰撞问题；

3)Shallot算法中，仅对公钥进行了一次哈希运算，在面对如今的高性能计算机，被寻找到碰撞的可能性很大.

这些事件威胁了现在通行的1024bit密钥、SHA1散列的安全性，Shallot算法存在安全隐患.

3.3 Shallot++算法

对Shallot++算法思想进行阐述，在此基础上提出Shallot++算法.

3.3.1 算法思想

为了解决Shallot算法中存在的两大问题,Shallot++算法主要将从以下3点进行改进.

1)RSA模数n=p×q是RSA算法安全性的核心，如果模数n被成功分解，则RSA公钥密码体制将被攻破[8,9]，Shallot++算法产生 RSA对象时，生成的大素数p与q大小均为1032bit，故模数n大小为2056bit，产生的RSA密钥长度符合2048bit，随着n的增大，因子分解的困难性也增大，这样严格符合RSA密码规格的要求.

2)在Shallot算法中，加密指数e是奇数，在满足RSA算法gcd(e,φ(n))=1的条件下，有效测试率P仅为79.68%.其中存在20.32%的无效碰撞测试，这不仅浪费了大量的时间，同时也降低了产生指定域名的命中率.加密指数e不能过小，一般采用不少于16位的素数，并且解密指数d要大于n0.3.Shallot++算法选用质数作为加密指数e，模数n的欧拉函数φ(n)=(p-1)×(q-1)为偶数，若φ(n)不是e的倍数，则gcd(e,φ(n))=1.选取e是不大于4294967295(十六进制为FFFFFFFF)的整数，e为Max内所有大于65537的质数，使用与Shallot算法中相同的RSA对象，根据式(1)、式(2)，计算可得有效测试率P为99.99%.

3)Shallot++算法对公钥进行双重哈希并行压缩的算法，如图1所示.第1轮将公钥(n,e)作为输入进行SHA-256运算，将第1轮哈希运算的输出作为输入，再次进行SHA-256运算，将第1轮运算输出结果的前40bit，与第2轮输出结果的后40bit组合，作为新的输入进行BASE32压缩.最后将输出的结果在后缀加上.onion作为洋葱域名.

图1 双重哈希并行压缩Fig.1 Double hash parallel compression

3.3.2 Shallot++算法

输入：指定的字符DomainName，生成符合指定字符的域名个数number

输出：公钥(n,e)，解密指数d，洋葱域名DomainID

1.Whilenumber>0 do

2. 产生2048位RSA对象(包含大素数p与q，模数n)

3.m=(p-1)×(q-1),e=2,test=0

4. Whilee≤Maxandnumber>0 do

5. 标记Max内所有e的倍数flage为1

6. While 1 do

7.e=e+1

8. ifflage≠1 Then/*未被标记的数为素数*/

9. break

10. End if

11. End While

12. ife>0xFFFFThen

13. 双重哈希并行压缩产生匿名域名

14. End if

15. test=test+1/*记录测试次数*/

16. if 产生的域名符合指定字符并且满足gcd(e,φ(n))=1 Then

17. 求解密指数d

18. ifd>n0.3

19. 输出公钥(n,e)，解密指数d，洋葱域名DomainID，测试次数test

20.number=number-1

21. End if

22. End if

23. End While

4 实 验

为了对比Shallot算法与Shallot++算法的性能与安全性，选用百度智能云服务器BCC进行编程实验，在保证实验软硬件环境相同的条件下，对实验的结果进行对比分析.

4.1 实验环境

实验采用百度智能云服务器BCC平台，系统为Windows Server 2016 Datacenter 64位，处理器为英特尔Xeon(至强)Gold6148 2.40GHz CPU 2核，内存为4G.集成开发环境IDE选为PyCharm，开发语言选用python3.

4.2 实验步骤和结果分析

Shallot算法与Shallot++算法的目的都是消耗尽可能少的时间计算出指定的域名.随着指定字符串个数的增多，生成符合要求的域名所需要的时间也呈指数增长.同时，通过测试不同的公钥来产生域名的时候具有偶然性，所以在指定的域名字符个数较少时，不能准确的反映算法的性能.

实验选用指定域名字符串为yzuedu(代表Yangzhou University Educational institutions).为了能更好的反映Shallot算法与Shallot++算法的性能，设计两个算法的输入分别为指定的域名字符DomainName与需要生成符合要求域名的个数N.算法的输出为N次，每次分别为符合指定字符串的.onion域名DomainID、公钥(n,e)、大素数p与q(保密)、解密指数d(保密)以及算法耗时和计算哈希次数.为了排除偶然性并且在理论上可行的计算时间内，获得指定域名字符串，分别输入4组测试数据，依次为(yzu,100)、(yzue,20)、(yzued,10)、(yzuedu,1).实验中产生的域名与私钥均已保存，由于进一步研究和安全性的需要，不在此公开，如需要可以后期提供.实验结果如表1所示.

表1 Shallot与Shallot++实验结果Table 1 Shallot and Shallot++ experimental results

第1组测试数据分析：Shallot算法比Shallot++算法多进行131138次碰撞测试，耗时却比Shallot++算法少117秒，因为Shallot++算法中，为了优化空间复杂度，节省空间并且减少CPU的I/O操作，算法在选取Max内所有素数时，并不将计算出的素数保存，每次计算Max内的素数要花费一定的时间，所以在指定的字符较少时，Shallot算法的耗时会优于Shallot++算法.

后3组测试数据分析：Shallot算法对比Shallot++算法的碰撞测试次数分别高于自身的49%、34%、33%，算法耗时分别高于自身的31%、23%、25%，Shallot碰撞测试次数和耗时均高于Shallot++是因为算法的有效测试率仅为79.68%，这不仅会有20.32%的无效碰撞测试，同时降低了生成域名的命中率.

为了对比两种算法的性能，对前4组数据进行进一步分析，在生成指定域名时，进行测试的次数越少则算法效率越高.在4次实验中，所进行的测试次数与计算时间如图2、图3所示.

图2 测试次数对比图Fig.2 Comparison chart of test times

随着指定域名字符的增多，虽然Shallot与Shallot++所需要的碰撞测试次数与运行时间都呈指数级增长，但是Shallot++算法的增幅低于Shallot算法.这表明指定域名字符越多，Shallot++算法的效率越高.

图3 所需时间对比图Fig.3 Comparison of time required

Shallot++采用双重哈希并行压缩的方式来产生域名，提高了算法防碰撞能力和域名的安全性.由于计算量的增加，单次碰撞的耗时将会增多，但Shallot++选取素数作为公钥中的加密指数e，将有效测试率提高到99.99%.当指定的域名字符较多时，Shallot++的总体耗时会明显少于Shallot算法.

5 总结与展望

为了使域名具有一定可读性、便于记忆，在Shallot算法的基础上，提出了一种有效的基于RSA的快速域名生成算法Shallot++，能够快速有效的生成指定的匿名域名.从算法时间效率上分析,Shallot++算法采用素数来作为加密指数e，这样极大的提高了e与模数n的欧拉函数φ(n)互素的概率，即将有效测试率从79.68%提高到99.99%，并且在指定较长字符的域名时，Shallot++算法的耗时明显优于Shallot算法.从算法安全性分析，采用素数来作为加密指数e，能够有效的预防模数n被攻击分解，同时，将Shallot算法中的SHA1改为SHA256，并且使用双重哈希并行压缩来产生域名，进一步增强抗碰撞能力.

虽然Shallot++算法相比Shallot算法能够更加快速有效地生成符合要求的域名，但是当指定字符数超过一定数量时，并不能从本质上解决巨大的时间消耗问题，提高哈希计算能力是提高算法效率的关键.Shallot++与Shallot都是基于CPU的，CPU适合做复杂的运算，而生成指定的域名需要将数亿次不同的公钥进行哈希计算，让CPU来完成重复的哈希计算会消耗大量的时间.

GPU相比CPU具有更多的核心，能够通过大量的并行计算提高浮点运算.下一步的研究工作重点是将算法的哈希计算移植到GPU上，同时采用具有更好地安全性与性能的ECC作为产生域名的公钥.可利用CPU先产生一部分公钥，将公钥拷贝到GPU中进行哈希运算，同时CPU继续产生公钥.当GPU完成哈希计算后，将结果返回CPU，CPU将计算的公钥再次拷贝到GPU，同时筛选符合要求的域名，完成后继续计算公钥.这样就能够充分发挥CPU和GPU各自的计算特点，进一步提高算法的计算处理性能.