借助信息技术提高学生的几何直观,帮助学生建立空间观念
严肃

随着科技的进步,信息技术已经广泛的应用于生活、生产等各个领域。它对教育行业的发展也有着巨大的影响。从“一根粉笔一块黑板”,到“PPT展示”,再到“交互式白板”的使用;从教师的“填鸭式”教学到“以学生为主体”的互动课堂、探究课堂等,这些变化都与信息技术息息相关。2011版的《中学数学课程标准》中指出:“在数学课程中应当注重发展学生的数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想”。这些都是数学核心素养的内容。《课标》中还提到:信息技术的发展,对数学教育的价值目标内容以及教学方式产生很大的影响,数学课程的设计与实施应根据实际情况合理的运用现代信息技术,要注意信息技术与课程内容的整合,注重实效,要充分考虑信息技术对数学学习内容和方式的影响,开发并向学生提供丰富的学习资源,把现代信息技术作为学生学习数学和解决问题的有力工具,有效的改进教与学的方式,使学生乐意并有可能投入到现实的、探索性的数学活动中去。由此可见,借助信息技术帮助学生提高学科核心素养是大势所趋,把信息技术融入学科教学是必经之路,那怎样借助信息技术帮助学生提升数学学科的核心素养呢?下面我以借助信息技术帮助学生提高几何直观,构建空间观念为例谈谈我的一些做法。
一、借助信息技术帮助学生识图、辨图,提高几何直观
几何直观主要是指利用图形描述和分析问题。借助几何直观可以把复杂的数学问题变得简明形象,有助于探索解决问题的思路,预测结果。几何直观可以帮助学生直观的理解数学,在整个数学学习过程中都发挥着重要的作用。
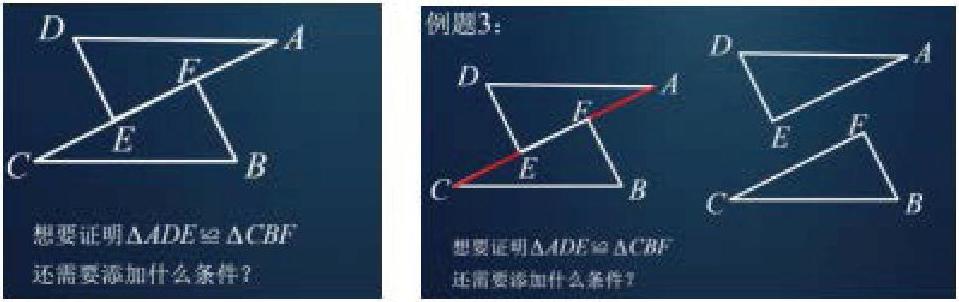
案例1:已知AD=BC,DE=BF,想要证明△ADE和△CBF全等,还需要添加什么条件?在分析问题的时候,可以借助希沃5的克隆功能,把两个三角形分离开来,这样学生就能比较直观的观察到想要证明全等的两个三角形的对应边和对应角分别是什么了?所以可以添加条件∠D=∠B(利用SAS进行证明),也可以添加AE=CF(利用SSS进行证明),还可以添加AF=CE(通过AF=CE,得到AF+FE=CE+EF,即AF=CE),但是有的同学认为AD=BC,DE=BF,AF=CE,则△ADE和△CBF就全等了,是利用了SSS定理。这显然是没有找准第三组对应边是什么。说明学生对图形没有一个正确的认识,而通过克隆功能把图形分解出来以后,就能一目了然的观察到对应边和对应角。
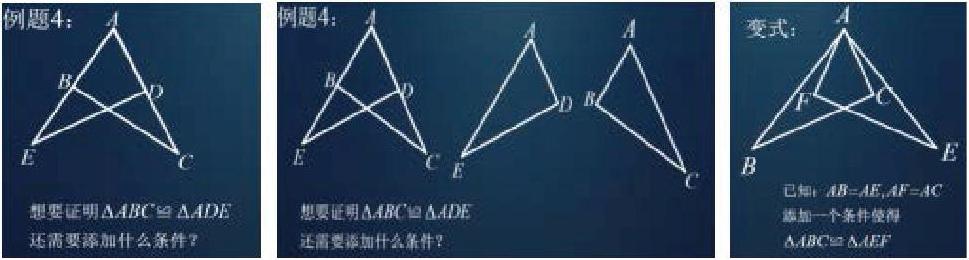
案例2:已知AE=AC,想要证明△ABC和△ADE全等,需要添加什么条件?这道题同样利用希沃5的克隆功能,将图形分解,把△ABC和△ADE分离开来,能够帮助学生快速找到两个想要证明全的三角形的对应边和对应角,这样就能顺利的找到需要添加的条件了。即使将题目进行变式,也不会慌乱。
这种借助信息技术将图形分离的方法能够帮助学生更直观的观察图形的特点,提高学生识图、辨图的能力,从而寻求出解题思路。
二、借助信息技术帮助学生构建空间观念,感知图形的运动变化
空间观念主要是指根据物体特征抽象出几何图形,根据几何图形想象出所描述的实际物体;想象出物体的方位和相互之间的位置关系;描述图形的运动和变化;依据语言的描述画出图形等。
案例3:已知:如图1所示△ABC和△CDE都是等边三角形,求证:AD=BE。若△CDE绕着点C旋转到图2所示位置AD=BE仍然成立吗?学生对于这种运动变化的题目一向是“丈二和尚,摸不着头脑”。讲解这类题目时,可以借助几何画板,度量出AD与BE的长度,让学生观察其相等的结果。再将△CDE绕着点C进行旋转,在旋转的过程中让学生一直观察AD与BE的长度变化,学生能发现,不论怎样旋转都有AD=BE成立。如果只是单纯的画两幅图形通过全等证明AD=BE,很多学生会觉得晦涩难懂,但是利用幾何画板,让图形动起来,就能更形象的感知图形旋转运动的过程中哪些量变了,哪些量没变,为什么AD与BE始终都是相等的。这种借助信息技术手段,帮助学生分析问题的方法,更能够帮护学生建立空间观念,感知图形的运动变化。
通过上面的实例不难看出,信息技术在帮助学生构建空间观念,提高几何直观感知方面有着不可替代的作用。
我也会继续深入学习信息技术,继续挖掘数学学科的特点,努力把信息技术与数学学科的特点相融合,让信息技术更好的为数学教学服务,通过信息技术手段帮助学生提高数学学科的核心素养。

