例谈学生数学技能的培养
余伟希
摘要:学习知识是一种内部思维过程,尤其是在数学学习方面尤其明显。教师在数学教学时,要做好数理、算理等思维指导,特别是教学应用题的时候,要教会学生在审阅题意、辨析数量关系,运用解法思维等环节,为此,要按学生的认识规律,引导学生学会先思后练,教师要授人以法,由旧引新地组织教学,要充分利用形、数等多种教学手段的结合,消除学生头脑中的思维单一性,培养思维的灵活性和发散性,使学生有效地掌握新旧知识的思维联系,培养他们的思维方法和自主创新能力。
关键词:思维训练 教学方法 数学技能
师者,传道授业解惑也。而善教者,使人得其法。故在传递知识的过程中,培养学生如何思维的方法,是数学教学的一项重要任务。学生学会思考问题、掌握寻求解决问题的方法比学会一个结论更重要。因为结论要在特定条件下才能运用,而思维方法的应用,就比它更具有广泛性。因此,我认为:应在多渠道的训练中培养学生的思维方法,注重思维的互动,以提高学生的解题和自学能力,使其创新思维及能力得到培养。我在数学教学中,作了这方面的探索。
一、启发思路,明晰算理,培养解题思维方法
学生解应用题的时候,能否结合题意,选用恰当的思维方法,辨析题中的数量关系,可看出学生解题思路是否正确。在教学应用题时,我让学生用最简要的文字写明关键步骤的算理,理清解题思路,有效地掌握新旧知识的思维联系,培养他们的思维方法和自主创新能力。当学习了义务教育教科书数学五年级上册P37的应用题例10后,在学生练习时就要学生写出算理才列式计算,同时进行变式练习进一步拓展学生解题思维:“某公司要生产手机54万部,前10天平均每天制造1.5万部,余下的要在20天完成,平均每天要制造多少万部?”一题,先列出自学提纲,让学生阅读分析:
(1)“平均每天修补多少本”是什么意思?
(2)求平均每天修补多少本,要具备什么条件?
(3)想一想,先算什么,后算什么。
然后在学生弄清题意的基础上让他们用简明的文字写出关键步骤的算理。
(1)要求平均每天修补多少本,就用剩下的数量除以指定的修补时间。
(2)先算剩下多少本。
(3)数量关系式:(总数量一两天共修补的数量)÷修补的时间通过这样的思考和练习形式,用合理的思维方法,辨析题中的数量关系,就可以学到解应用题的一般方法。
二、巧用旧知,潜移转化,指引逻辑思维方向
学习是学生的一种内部的过程,要教会学生学习,就要按学生的认识规律,由旧引新地组织教学。要学习新的知识,往往是通过实物教具、学具或实例,使学生各种感官齐参与,并在旧知识思维基础上,经分析综合,抽象概括出概念、法则、性质等,并进行简单的判断和推理才能掌握。此过程就充满思维的互动性,故在教学中要巧用旧知,使新接触的知识通过“温故”,在思考、辨析的过程中得到潜移转化为“新知”。
如学习“梯形的面积”,以往是教师演示教具,然后抽象概括出求面积的公式。这只注意老师的教,忽视了学生主体的地位。现在我让学生在课前准备两个大小相等的全等梯形,上课时启发学生想一想:
(1)我们已经学过什么几何图形?
(2)你能不能把做好的两个梯形拼成已学过的一种图形?
(3)可以拼成什么图形?原来梯形的底和高与拼成的图形的底和高有何关系?
学生边想边操作,很快就发现可以拼出四边形、长方形和正方形。在此基础上,再引导学生观察原来梯形的底和高与新图形的底和高有什么关系。通过对比、分析,使学生理解:所拼成的平行四边形的底就是原来梯形上下底之和,其高就是梯形的高。所拼成的长方形的长就是原来梯形的上下底之和,宽就是梯形的高。并看到一个梯形面积就是所拼成的新图形面积的一半。于是推导出梯形面积的公式:
(上底十下底)×高÷2
这样可使学生的直覺动作思维向抽象逻辑思维过渡。既理解这公式的含义,又明白其由来。
此外,在学习那些与旧知识有联系的新知识时,找准新旧知识的联系点,在关键之处加以点拨,既巩固旧知又利于思维能力的培养。
三、创设练习情境,培养思维的灵活性
创设练习情境,就是根据所授知识核心内容,编撰一些能够克服思维定势的题目,利用形、数等多种教学手段的结合,消除学生头脑中的思维单一性,培养思维的灵活性和发散性。
如编撰这样一道题:“一个打字员要打21000字的书稿,计划用12小时,由于提高了打字速度,每小时多打了250字,打完这份书稿实际用了几小时?”
根据原题的条件,作如下变式训练,以培养学生思维的灵活性“一个打字员要打21000字的书稿,计划用12小时,由于提高了打字速度,每小时多打了250字?”(要求根据给出的条件,在指定的三个算式前面,加上相应的问题。)
(1)21000÷(21000÷12 + 250)
(2)12-21000÷(21000÷12 + 250)
(3)21000÷12 + 250
学生要依据三个算式所呈现的不同的数量之间的关系,在辨析比较中填写三个不同的问题。这样,学生思维活跃的幅度大,知识间联系的面宽,从而培养了思维的灵活性。
另外,对一些可给学生的思维留有纵横驰骋余地的题目,尽可能鼓励他们进行一题多解。
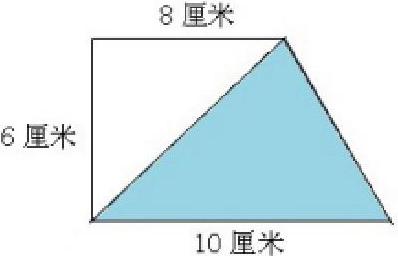
如求下图中阴影部分的面积:
引导学生认真观察,联系旧知,变通地列出式子计算,部分学生写出一种或两种式子,少数写出四种以上,最多的写出如下的五种解法:
(1)10×6÷2(直接求阴影面积)
(2)10×6÷2(求长方形面积的一半)
(3)(8+10)×6÷2-8×6÷2(梯形面积 - 空白三角形面积)
(4)10×6-8×6÷2-(10-8)×6÷2(长方形面积 - 两个空白三角形面积)
(5)10×6-8×6÷2-(10-8)×6÷2(长方形面积 - 空白三角形面积 - 部分阴影的三角形面积)
实践证明,注重思维的互动,既提高了分析问题的能力,沟通了知识间的内在联系,也发展了求异思维能力,同时训练了学生思维的周密性和多向性,可以使智力水平不同层次的学生都能获得施展的机会,也是给思维灵活的学生以鼓励,培养他们大胆探索,积极创新的思维能力,促进学生应用能力的发展。

