叶巴滩高拱坝坝肩稳定分析及其加固效果评价

张 芮 瑜，陈 媛，张 林，刘 子 安，杨 宝 全，董 建 华，张 冲

(1.四川大学 水力学与山区河流开发保护国家重点实验室，四川 成都 610065； 2.四川大学 水利水电学院，四川 成都 610065； 3.中国电建集团成都勘测设计研究院有限公司，四川 成都 610072)

在水电工程建设中，拱坝作为一种常见的水工建筑物，具有良好的超载能力、安全性及经济性等特点。我国已建或在建的高拱坝工程，如锦屏一级、小湾、溪洛渡、乌东德，白鹤滩、叶巴滩等，普遍具有坝址区蚀变带、断夹层、节理裂隙、软弱结构面发育等复杂地质构造的特点[1-3]，坝基及坝肩的适当处理关乎大坝的整体稳定安全性，尤其对于坝高超过200 m的特高拱坝，需要对专门的问题进行研究[4]。

当前，国内外对高拱坝坝基坝肩加固处理开展了很多重要研究并取得大量研究成果[5-7]。其整体稳定安全性分析方法主要包括原型观测法、数值计算法及地质力学模型试验法。胡波[8]等基于原型监测，分析评价了小湾特高拱坝坝肩软弱带置换效果；杨强[9]等采用有限元软件获得拱坝坝肩破坏形态、过程并对整体稳定安全进行分析；刘耀儒[10]等采用地质力学模型法对小湾拱坝坝体裂缝对受力及稳定的影响进行研究；张林[11]等采用地质力学模型试验法，获得拱坝坝肩失稳的破坏过程、破坏形态、破坏机理及整体稳定安全度。以上3种方法对高拱坝的整体稳定性分析具有重要参考价值。原型观测属于事后观测，难以对高拱坝稳定进行预测并提前采取加固措施。有限元分析广泛应用于多种行业的工程数值模拟与计算机辅助工程中，具有重要的工程意义。由于高拱坝所处的地质环境、地应力条件通常十分复杂，通过地质力学模型试验研究高拱坝的安全稳定，能够模拟坝肩复杂地质构造，直观显示坝肩的破坏区域及薄弱环节，同时能够考虑到多种因素对坝肩稳定的影响，是解决复杂地质条件下坝基坝肩稳定分析的重要手段[12-13]。实际工程建设中，往往结合多种方法研究高拱坝的稳定性，相互验证、互为补充。

叶巴滩高拱坝坝基、坝肩地质条件复杂，稳定安全问题突出。针对该问题，本文开展了数值与物理模拟分析坝肩加固处理效果的研究。首先，基于有限元数值计算分析叶巴滩拱坝在天然地质条件下的坝肩稳定性，揭示其坝肩薄弱环节，并针对性提出加固措施，对加固后的叶巴滩坝肩整体稳定性进行有限元计算及三维地质力学模型试验。通过对比分析获得拱坝坝肩变形特性、失稳破坏过程、破坏形态与破坏机理，对坝肩整体稳定安全性及加固措施的有效性进行分析评价。

1 工程概况及地质条件

叶巴滩水电站位于四川省白玉县与西藏贡觉县境内，是金沙江上游重要梯级电站。电站正常蓄水位为2 889 m，电站装机容量2 240 MW，年发电量102.36亿kW·h。电站枢纽建筑物由混凝土挡水建筑物、泄洪消能建筑物及引水发电三大系统组成。混凝土双曲拱坝坝高217 m，坝顶高程2 894 m。坝址区为典型的“V”形河谷，河谷狭窄，两岸总体较为对称，坝区岩性相对均一且结构较完整。叶巴滩地质平面图如图1所示。

图1 叶巴滩水电站地质平面Fig.1 Geological plan of Yebatan Hydropower Station

叶巴滩拱坝坝址区破裂结构面发育，断层破碎带宽度大于1 m的Ⅱ级结构面主要有F1，F2，F3，F4等4条，延伸长度数百米至数千米；Ⅲ级、Ⅳ级结构面约460条，延伸长度数十米至数百米。影响坝肩稳定的主要不利地质构造有：左右岸及河床位置分布的贯穿性伴生断层F1、F2，其在河床坝基部位埋深较浅，距离坝踵较近；两岸坝肩及抗力体发育有f24，f22，F3，f29等断层，f24断层在建基面2 840～2 860 m高程出露，与F2，f21，f7等结构面相互切割，削弱了两岸抗力体的完整性；f22断层斜切左岸坝肩，在拱坝左岸建基面的2 870～2 880 m高程出露，与挤压带g23-4及优势节理裂隙J5-2组合形成滑移块体；f 29断层在建基面2 810～2 820 m高程出露，走向及所处位置对右坝肩不利，是右坝肩整体稳定的控制性断层，并与优势节理裂隙J5-3组合形成滑移块体，存在滑移失稳的趋势。F3断层延伸长度大于1 000 m，泥化条带连续发育、厚度大。这些地质缺陷影响坝基变形和坝肩抗滑稳定性，对拱坝及地基的整体稳定产生不利影响。坝址区岩体及结构面物理力学参数如表1所示。

表1 叶巴滩拱坝坝址区岩体和结构面主要物理力学参数Tab.1 Main mechanical parameters of rock mass and structure planes at dam site of Yebatan arch dam

2 天然地基条件下有限元计算分析

2.1 有限元计算模型

叶巴滩拱坝及坝肩岩体三维有限元模型如图2所示。其模拟范围为：以拱坝坝底轴线为中心，往上游约1.5倍坝高，往下游约2.5倍坝高，往左右两岸各约2倍坝高，往地基方向约1倍坝高，往坝顶方向模拟至3 050 m高程，下距坝顶156 m。模拟范围为962 m×760 m×600 m(横向×纵向×高度)。模型x方向坐标为横河向，向左岸为正；y方向坐标为顺河向，向上游为正；z方向坐标为竖直向，向坝顶为正。计算模型为理想弹塑性模型，地基及岩体采用D-P准则，计算模型共离散为161 836个节点和146 281个六面体单元，模拟的断层和软弱夹层主要有：F2(F1)、F3、f 24、f 22、f 29，断层及岩体计算参数同表1。

图2 叶巴滩拱坝三维有限元模型Fig.2 3D FEM model of Yebatan arch dam

有限元计算采用超载法，主要考虑超标洪水对工程的影响[14-16]。超载法评价中将大坝发生初裂、非线性大变形以及极限破坏时的安全系数分别用起裂超载安全系数K1、非线性变形超载安全系数K2、极限超载安全系数K3来表示，反映大坝在一定荷载作用下，大坝与基础联合作用抵抗荷载的能力[13]。作用荷载主要为自重及上游水压力，忽略下游水压力及温度荷载，在坝体上游面施加正常水荷载(1P0)，模拟坝体坝肩在正常工况下的运行情况，并以0.1P0步长逐步超载，直至计算不收敛或出现塑性贯通，坝与地基出现整体失稳破坏。

2.2 计算结果分析

2.2.1坝体变位

坝体的顺河向以向下游变位为主，坝体的最大变位发生在坝顶拱冠梁处，符合拱坝坝体变位规律。选取顺河向变位值最大的坝顶2 894 m高程为典型高程平面，分别获取左右拱端、左右半拱及拱冠梁下游面顺河向位移值，如图3所示。正常工况下，即KP=1.0时，左右半拱顺河向变位基本一致，坝体变位对称性较好；进入超载阶段，随超载系数KP增加，坝体顺河向变位进入非线性变化，坝体右半拱顺河向变位值逐渐大于左半拱；当KP=7.0时，坝体变形较大且不对称性较明显，右半拱顺河向变位与左半拱变位差为113.2 mm。

图3 不同超载倍数下2 894 m高程拱圈下游面顺河向位移δy分布曲线Fig.3 Distribution curves of displacement along river on downstream dam surface at EL.2 894 m under different overloading coefficient

2.2.2坝肩变位

在2 790～2 870 m高程附近，坝肩横河向和顺河向变位值都相对其它高程较大。沿拱推力方向选取2 790 m高程的左、右坝肩各5个典型测点，研究在拱推力传递方向的坝肩及主要结构面的变形特性。坝肩典型测点位置及顺河向变位与超载系数的关系如图4所示。从变位分布整体上看，左、右坝肩位移值在拱端附近最大，往远离拱端方向逐步递减，并随超载倍数增加而增大。但随着超载倍数的增加，右岸拱端附近岩体顺河向变位增长较左岸拱端附近岩体快，呈现出变位不对称现象，与坝体在超载后期变位不对称相一致。断层f29及断层f24两侧变位相差较大，断层强度参数低，岩体完整性较差，对拱推力的传递造成影响。

图4 坝肩典型测点顺河向位移δy与超载系数KP关系曲线Fig.4 Typical curves of displacement along river δy vs.overloading factor KP

在正常工况下，左右坝肩断层两侧典型测点位置及位移值如图5所示。由图5可知：左坝肩f24断层2号测点顺河向及横河向位移均大于3号测点，f22断层4号测点横河向往山体里变位，5号测点横河向往河床变位，且顺河向位移小于4号测点。由此可见，以上两个断层均有相对错动，对坝肩抗滑稳定性影响较大；右坝肩f29断层6号、7号测点横河向均向山体里变位，顺河向均向下游变位，但两测点位移值相差较大，断层两侧的岩体存在相对错动。F3断层距拱端较远，受到的剪切与挤压作用不大，变位值较小，对坝肩抗滑稳定性影响较小。另一方面，断层F2顺河向变位在坝基高程2 677 m最大，并随着超载倍数增大，断层两侧测点顺河向位移差值明显增大，且F2距离坝踵较近，对坝基防渗有一定影响。

2.2.3塑性区发展

在正常工况KP=1.0时，坝基附近没有塑性区产生，各断层受挤压局部进入塑性状态；当KP=1.3时，坝基上游侧出现塑性区，坝体底部附近的断层F2出现较明显的塑性区分布；当KP=3.0时，坝基下游侧出现塑性区分布，坝基上游侧及F2断层的塑性区扩大；当KP=4.0时，坝体下游面左右拱端出现塑性区，坝基上游侧塑性区与断层F2的塑性区连通；当KP=5.0时，坝体上下游面的塑性区连通，坝基塑性区扩大；当KP=6.0～7.0时，塑性区在坝体、坝肩迅速发展，最终坝体大部分进入塑性区，坝肩上下游塑性贯通，此时坝体破坏。

图5 正常工况下两岸坝肩结构面附近测点及位移值(KP=1.0)Fig.5 Displacement of measure points near structural planes in both abutments under normal condition as KP=1.0

综合分析天然地基条件下塑性区发展过程，结合坝体及坝肩、断层变位等情况，得出天然地基下叶巴滩拱坝超载安全系数为：K1=1.3，K2=3.6～3.8，K3=7.0。计算所得典型高程平切面等效塑性应变值分布如图6所示，其中灰色为超过最大值0.8×10-3部分。由图可知，塑性区主要分布在靠近拱端坝肩位置，右坝肩f29断层及左坝肩f24断层附近塑性应变值较大，破坏程度较严重。

2.3 坝肩稳定性及加固处理措施

由不同超载倍数下变位情况及塑性区发展可知：由于两岸坝肩内发育的断层强度较低，与节理裂隙相互交错，破坏了坝肩抗力体的完整性，使拱推力的传递受阻，对坝肩变形影响较大。断层f29走向及所处位置对右坝肩不利，其承受拱推力较大，岩体强度低，在荷载作用下容易受压变形，进而导致右半拱及右坝肩的变位明显较左岸变位大。并且断层f24、f29在建基面附近出露，影响坝体的受力及变形性态。从f24、f29断层两侧岩体受力后位移方向上看，在左、右坝肩拱推力较大区域有向河谷滑移趋势，结构面两侧产生相互错动，对拱坝的抗滑稳定性产生不利影响。断层F2距离坝踵较近，对坝基防渗有一定影响，且断层宽度大、性状差、变形模量低，坝基局部变形较大，需结合坝肩变形稳定和坝基防渗进行综合处理。综上可知，坝肩附近存在的多条断层，由于断层强度低，承受拱推力荷载较大，产状及位置对拱坝的抗滑稳定性不利，成为了影响叶巴滩拱坝坝肩整体稳定的薄弱环节。

图6 不同超载系数下2 790 m高程平面塑性破坏区域Fig.6 Plastic failure zone of arch dam and abutment at EL. 2 790 m under different overloading factor

针对天然坝基的这些薄弱环节，对叶巴滩拱坝坝基、坝肩进行加固处理：对F2断层在坝基出露处附近进行混凝土置换，对右岸坝肩断层f29在建基面出露的2 790～2 840 m高程附近进行混凝土刻槽置换，对左岸坝肩断层f24在建基面出露的2 830～2 890 m高程附近进行混凝土刻槽置换。叶巴滩拱坝坝肩加固措施如图7所示。

图7 坝肩加固处理措施Fig.7 Reinforcement of dam abutment

3 加固后的坝肩稳定性分析及加固效果评价

3.1 有限元数值计算

加固地基条件下，有限元计算除增加加固处理措施外，计算条件与天然地基条件下一致。加固后，不同超载倍数下2 894 m高程坝体左右拱端、左右半拱及拱冠梁下游面顺河向位移如图8所示。总体上看，拱坝坝体变位减小，在不同超载倍数下，左、右半拱位移差值均有所减小，减小率约25%～30%，表明坝体变位左右对称性得到改善。加固前后各典型高程拱冠梁顺河向位移如图9所示。当KP=1.0时，坝顶拱冠梁位移减小5.6%，底部位移减小5.6%；当KP=3.0时，坝顶拱冠梁位移减小6.24%，底部位移减小7.57%；当KP=5.0时，坝顶拱冠梁位移减小6.61%，底部位移减小8.45%；KP=7.0时，坝顶拱冠梁位移减小7.8%，底部位移减小9.6%。

图8 加固后2 894 m高程拱圈下游面顺河向位移δy分布曲线Fig.8 Distribution curves of displacement along riverδy on downstream dam surface at EL.2 894 m after reinforced

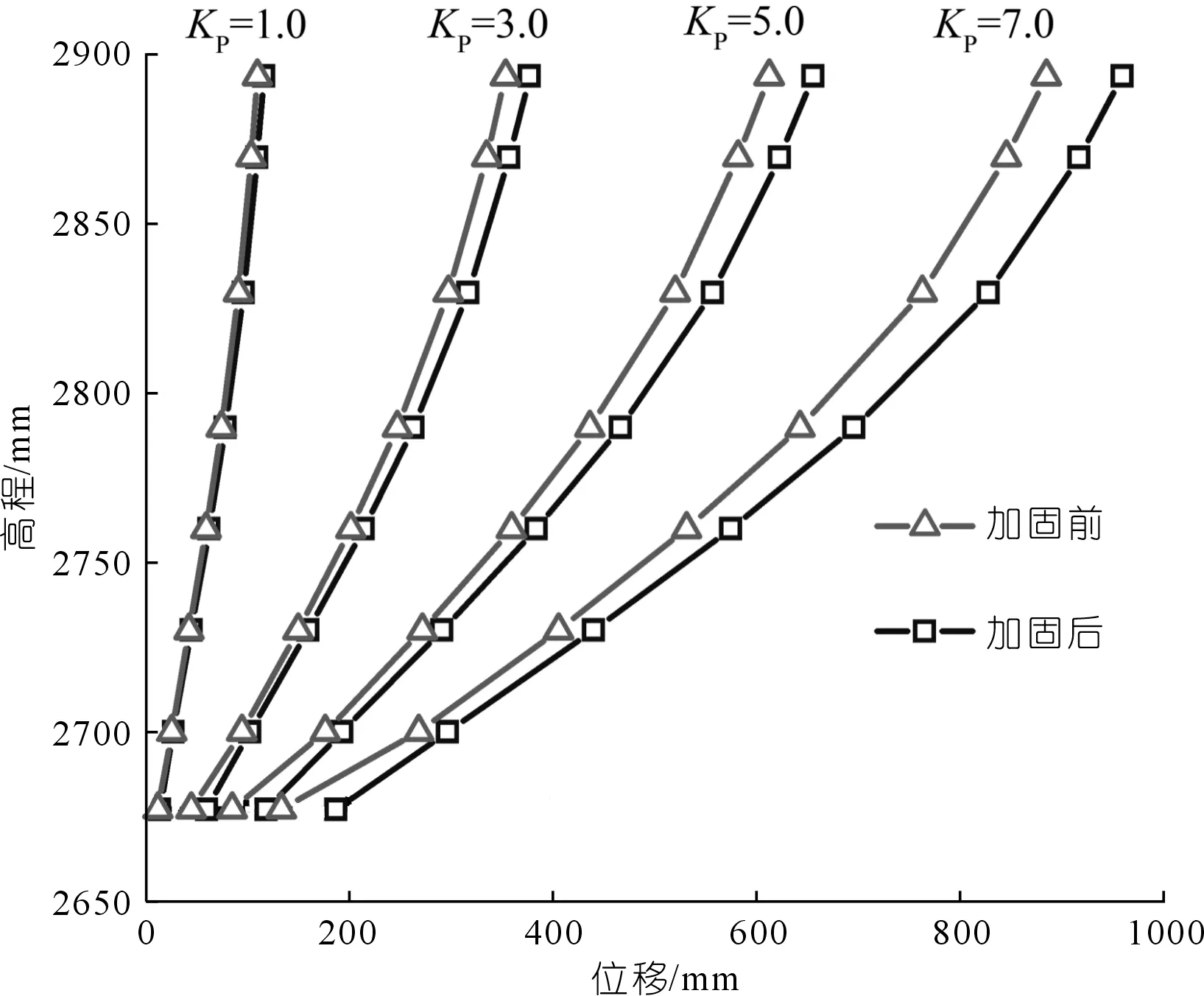
图9 加固前后典型高程拱冠梁顺河向位移δy对比Fig.9 Comparison of displacement along river δy of crown cantilever at typical elevation before and after reinforced

正常工况下，坝肩岩体位移减小较明显：天然地基条件下最大顺河向位移为24.1 mm；加固地基条件下最大顺河向位移为21.3 mm，减少11.6%。天然地基条件下左右坝肩最大横河向位移分别为9.5，8.2 mm；加固地基条件下左、右坝肩最大横河向位移分别为8.2，7.4 mm，位移值分别减少13.7%，26.0%。加固后，断层附近横河向及顺河向变位减小，且断层两侧相对位移减小，其相对位移减小率约10%～30%，断层错动现象得到明显改善，对增强坝肩抗滑稳定效果显著。拱坝坝肩f29断层上下游两侧6号、7号测点的横河向变位情况如图10所示。

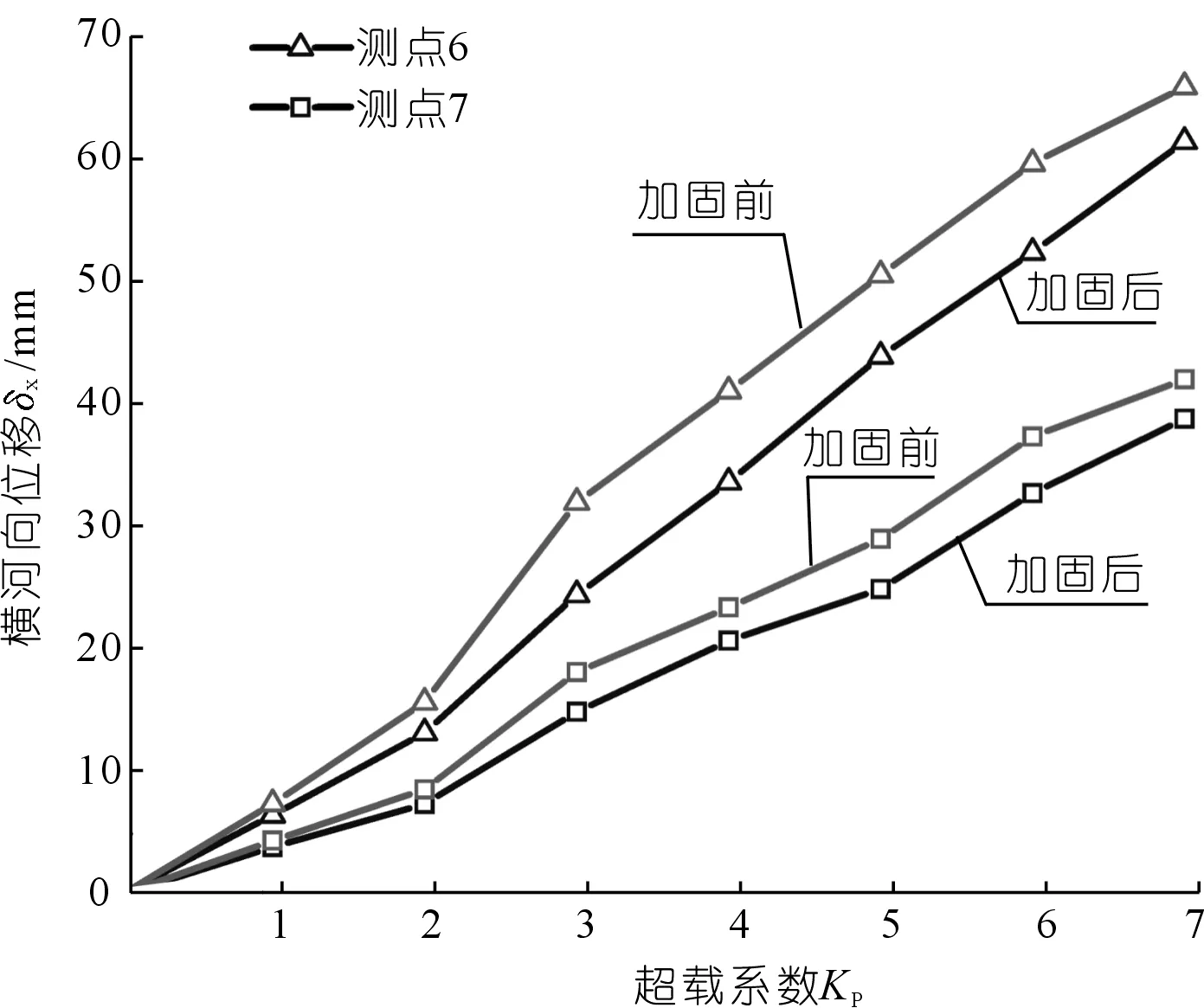
图10 加固前后f29断层横河向变位δx与超载系数KP关系曲线Fig.10 Curves of displacement across river δx near fault f29 vs.overloading factor KP before and after reinforced

3.2 地质力学模型试验

地质力学模型试验需要满足破坏实验的相似要求，即几何、应力应变、地质构造面抗剪强度及力学相似[17-18 ]。本次叶巴滩拱坝地质力学模型试验采用几何比相似系数CL=200。根据相似理论，其他主要相似系数如下：Cγ=1，Cε=1，Cf=1，Cμ=1，CL=CE=Cσ=CC，CF=CσCL2=CγCL3。其中CE，Cε，Cγ，CL，Cσ，CF分别为变形模量、应变、容重、几何尺寸、应力及荷载的相似比，Cμ，Cf和CC分别为泊松比、摩擦系数及凝聚力的相似比。混凝土、岩体和主要结构面物理力学参数由表1通过相似关系换算得到。模型模拟范围除向上游约1倍坝高，其余范围与有限元计算模型相同。模型模拟了两岸地形、主要地质条件、贯穿性断层、左右坝肩及抗力体各类岩体及断层、节理裂隙、挤压破碎带等。

根据模型相似材料的物理力学参数，本次试验从力学相似角度开展大量的材料试验，研制出与原型材料相似的模型材料。叶巴滩拱坝模型材料以重晶石粉为主，少量石膏粉为胶结剂，水为稀释剂，并掺适量的添加剂等；岩体材料的模拟采用重晶石粉为主，高标号机油为胶结剂，并掺入适量添加剂等。试验中，根据相似原理得到的模型材料参数，制定多种配比压制成的岩体试件，使用MTS-815材料特性试验机进行测试，得到不同配比下各组岩体的强度参数(cm和fm)及变形模量Em等。并根据测试结果不断调整配合比，直至达到相似要求，确定各类岩体最终配合比。结构面模型材料的研制根据其抗剪断强度的相似关系，采用重晶石粉、机油及添加剂，并选用不同摩擦系数的薄膜材料配合使用，实现对结构面抗剪断强度的模拟。

三维地质力学模型试验模拟的荷载与有限元计算保持一致，上游水荷载采用油压千斤顶进行分层分级加载。模型试验过程如下：首先对模型进行预压，然后逐步加载至一倍正常水荷载P0，最后按照0.2P0的步长对上游水荷载进行超载，直到拱坝与地基出现整体失稳破坏趋势。

加固后的叶巴滩三维地质力学模型试验与有限元计算得到的变形分布规律基本一致。试验获得了坝体坝肩的表面变位、结构面内部的相对变位、坝基坝肩失稳过程及破坏模式等，在坝肩断层出露处获得的测点变位如图11所示。超载初期，坝肩变位不大，随超载倍数的增加，变位值逐步增大。在KP=3.6～4.0时，大部分坝体变位曲线、应变曲线出现较大的波动和明显的拐点，此后测点变位变化幅度增大。超载系数KP=5.0时，模型右坝肩附近测点135号位移值为100.0 mm，有限元模型计算位移值为98.4 mm，物理和计算模型变位规律基本一致，变位值相近，相互验证互为补充，研究成果可靠，模型最终破坏形态如图12所示。

图11 模型中断层出露处顺河向变位δy与超载系数KP关系曲线Fig.11 Curves of displacement along river δy vs.overloading factor KP at fault outcrop in model test

3.3 稳定安全性及加固效果评价

有限元计算结果显示：坝基坝肩进行加固后，KP=1.5时，坝基中部高程上游侧出现塑性区；KP=3.0时，坝基下游侧出现塑性区，上游侧塑性区扩大；KP=4.0时，坝体上游侧和下游侧出现塑性区；KP=6.0～7.0时，坝基上下游塑性区贯通，塑性区分布范围扩大。数值计算及模型试验获得的叶巴滩拱坝与地基整体稳定安全系数见表2。

图12 模型最终破坏形态Fig.12 Final failure pattern of geological model

表2 有限元计算及模型试验稳定安全系数Tab.2 Safety factors of finite calculation and geomechanical model test

综合分析有限元计算及模型试验结果可知，对建基面附近出露的断层F2、f29、f24采取混凝土刻槽置换的处理措施取得了良好的加固效果，主要表现在以下几方面：① 改善了坝体的受力状态，使得坝体左、右岸变位较对称，变形协调性和一致性得到改善，坝体及坝肩变位均有所减小；② 坝肩和坝基塑性破坏范围减小，坝肩槽破坏主要集中在未进行混凝土置换的区域和靠上游侧的岩基，坝肩破坏范围减小；③ 拱坝的初裂安全系数K1和大变形安全系数K2得到提高，即坝肩出现初裂和发生大变形屈服时的荷载超载倍数增加，坝基的承载能力和坝肩的整体稳定安全性得到有效提高。

4 结 论

(1) 天然地基条件下，叶巴滩拱坝坝身与坝肩变位较大，左、右岸坝体与坝肩变位呈现明显不对称特性；拱端附近发育的断层f29、f24、f22等产生相互错动，坝肩存在抗滑稳定安全问题；断层F2距离坝踵较近，对坝肩变形稳定和坝基防渗有一定影响。针对天然坝基的这些薄弱环节，提出对叶巴滩拱坝采用的主要加固措施为：对F2断层在坝基附近进行混凝土置换，对左右岸坝肩断层f29、f24在建基面出露处进行混凝土刻槽置换。

(2) 综合分析试验与计算成果可知：刻槽置换的加固措施改善了坝体受力状态与变形特征，坝体左右岸变位对称性明显提高，坝体变形较协调，坝肩破坏范围有所减小。地基加固处理后，拱坝与坝肩发生起裂、大变形屈服时的荷载得到提高，增大了拱坝与地基的初裂安全系数K1和大变形安全系数K2，坝基坝肩整体稳定性得到提高。

(3) 在加固地基条件下，三维地质力学模型试验所得变位值与计算变位值相近，变形分布规律基本一致，模型试验与有限元计算相互验证，互为补充，研究成果可靠。