基于预处理的快速幂算法及其实现*
段学松,曲中水,江绪桢,吕昌昊
(哈尔滨理工大学 计算机科学与技术学院,黑龙江 哈尔滨 150080)
1 概述
快速幂算法,即快速计算一个数或者矩阵的幂次的算法,一直是加密算法中的重要算法,并且在数论中有着相当广泛的应用,更是算法竞赛中最常遇到的问题,尤其在线性齐次递推数列[1]的求解上。例如常见的斐波那契数列[1]第n 项的计算,通过构造转移矩阵[1]和快速计算矩阵幂次[1]的方式能够大大降低计算线性齐次递推数列的时间复杂度。但是随着矩阵的行数和列数不断增加,每一次矩阵乘法会变得相当耗时,对于稀疏矩阵,虽然存在优化算法[2],甚至存在优化算法的硬件实现[3],但是如何减少矩阵乘法计算的次数变得极其重要。目前计算快速幂,最常用的算法是二进制拆分法[4],但是对于一个固定的数或者是固定矩阵的幂次来说,二进制拆分法并没有保留每次拆分的过程,导致拆分的过程会做大量的重复计算。因此对于固定的数或者固定矩阵的幂次,可以预处理部分数据,达到减少重复运算,降低算法时间复杂度的目的。
2 传统的二进制拆分快速幂算法概述
2.1 二进制拆分法的原理
计算an,传统的快速幂算法的核心思想是二进制拆分。令m 为n 在二进制下最高位1 的位置,我们对n 进行二进制拆分,则有:

通过乘法原理,可以得到:
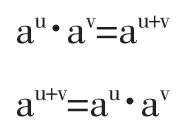
综上,可以得到:

其中,ei是n 在二进制下第i 位的值,例如当n=13的时候,n 的二进制形式为:(1101)2,最高位 1 的位置 m=4,对n 进行二进制拆分得到的结果为:
2.2 二进制拆分快速幂算法的时间复杂度与空间复杂度分析
T(n)=O(log2n)
由于二进制拆分快速幂算法用迭代实现,在计算的过程中用于存储计算用到的空间是常数级别的,因此二进制拆分快速幂算法的空间复杂度为:
S(n)=O(1)
如果计算k 次,总时间复杂度为:
T(n)=O(klog2n)
金坛区于2016年启动长荡湖清淤工程,在外源污染有效治理和控制的前提下,通过对长荡湖湖区污染底泥实施生态清淤,有效削减底泥内源污染,促进湖泊水体水质改善,为长荡湖水生态修复奠定基础。
总空间复杂度为:
S(n)=O(1)
2.3 二进制拆分快速幂算法的C++实现

图1 二进制拆分法的C++实现
2.4 多次计算时二进制拆分法的重复运算
当利用二进制拆分快速幂算法多次计算相同底数的幂次时,存在大量的冗余计算。例如:

3 基于预处理的快速幂算法
3.1 基于预处理的快速幂算法原理
首先我们用a mod b 表示a 对b 取余数。
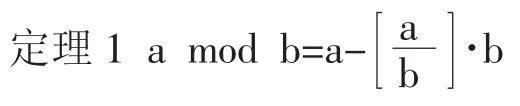
证明 由取余运算的性质[5]可得,定理1 成例。
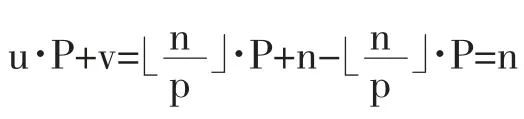
证毕。
根据定理2 以及乘法原理可得:

由于 u∈[0,P],v∈(0,P),因此可以在计算快速幂前预处理出 a0,a1,a2…aP-1,aP以及(aP)0,(aP)1,(aP)2…(aP)P-1,(aP)P并存储起来,每次计算an时,首先计算出以及v=n mod P,之后从提前预处理的数据中选择(aP)u和av进行一次乘法运算即可得到an的结果。
3.2 基于预处理的快速幂乘算法的时间复杂度与空间复杂度分析
3.2.1 预处理过程时间与空间复杂度分析
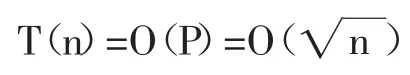
因为通过预处理能够得到aP,因此,预处理(aP)0,(aP)1,(aP)2…(aP)P-1,(aP)P的时间复杂度:

所以,预处理的总时间复杂度:
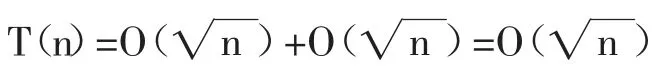
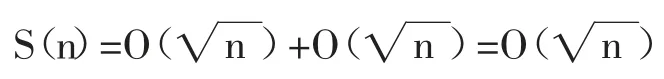
3.2.2 计算快速幂的时间与空间复杂度分析
在计算快速幂的过程中,由于P,u,v 的计算消耗是常数级别的,而计算查表计算一次乘法的时间复杂度也是常数级别的,因此计算快速幂的时间复杂度:
T(n)=O(1)
计算过程中临时变量的存储空间都是常数级别的,因此计算快速幂的空间复杂度为:
S(n)=O(1)
3.2.3 计算k 次相同底数的an的总体时间空间复杂度分析
预处理的目的是去除重复运算,对于相同的底数,多次计算快速幂只用进行一次预处理操作,k 次计算快速幂的总体时间复杂度是:

总体空间复杂度为:

3.3 基于预处理的快速幂乘算法的C++实现

图2 基于预处理的快速幂算法的C++实现
4 结束语
本文分析了二进制拆分快速幂算法的缺点,并针对相同底数的多次快速幂运算,提出了一种基于预处理的快速幂算法,通过预处理少量的数据,将时间复杂度为O(klog2n)求幂的算法优化至并给出了该算法的时间复杂度与空间复杂度的分析以及C++编程实现,为求解快速幂提供了新的思路。今后,随着程序设计应用的不断深入以及人们对算法的研究,更多更复杂的数学问题必定会迎刃而解。

