基于等价输入干扰滑模观测器的磁悬浮球系统模型预测控制

王军晓,陈林杰,俞 立

(浙江工业大学信息工程学院,浙江杭州 310023)

1 引言

磁悬浮是一种通过非接触模式悬挂物体的技术,该技术消除了系统中运动部件和静止部件之间的机械接触,因此它具有无摩擦、无磨损、无噪音等优点[1].目前,磁悬浮技术在工业领域得到了广泛的应用,如高速磁悬浮列车、磁悬浮轴承、磁悬浮储能飞轮、磁悬浮直线电动机[2-5].然而,磁悬浮系统是一个典型的强非线性,开环不稳定系统,且易受外部干扰的影响,这使得磁悬浮系统的高性能控制成为一个挑战.为此,学者们在磁悬浮系统的控制策略上做了大量的探索和研究,如比例-积分-微分(proportion integral differential,PID)控制[6]、自抗扰控制[7]、滑模控制[8]等,这些方法在不同方面提高了磁悬浮系统的控制性能.

模型预测控制(model predictive control,MPC)不仅可以通过滚动优化获得令人满意的控制性能,而且还具有显示处理约束的能力[9-11],使其成为继PID控制之后在控制工程中获得广泛应用和认可的先进控制技术之一[12].目前,模型预测控制已成功应用于汽车[13]、地铁[14]、电机[15]等领域.但是,系统模型不确定性和外部干扰总是给闭环控制性能产生不良影响,而包括模型预测控制在内的许多先进控制算法仍是通过经典的反馈控制设计来抑制扰动的影响,这就导致了闭环系统不得不在牺牲其它控制性能的前提下提高抗扰动性能[16-17].积分模型预测控制(integral model predictive control,IMPC)[18]常被用来抑制干扰和模型不确定性,该方法通过将状态方程改写为增量形式引入积分作用,因此能够较好地抑制常值扰动.然而,当系统受到时变扰动的影响时,稳态跟踪误差通常是不可避免的.除此之外,利用积分作用来抑制扰动的做法将付出牺牲闭环系统其它控制性能的代价,如跟踪性能和鲁棒性等[16].作为一种实用的替代方法,基于扰动观测器的控制(control of disturbance observer,DOBC)方法能够有效地补偿外部干扰和模型不确定性对控制系统的影响[19].受此启发,结合模型预测控制(MPC)和扰动观测器(disturbance observer,DOB)的控制结构能够在不牺牲标称性能的前提下抑制扰动.文献[20]中结合MPC和扩张状态观测器(extended state observer,ESO),提高了液压系统对模型不确定性和干扰的鲁棒性,文献[21]中针对非线性系统设计了一种基于非线性干扰观测器(nonlinear disturbance observer,NDOB)的非线性模型预测控制(nonlinear model predictive control,NMPC)方法,文献[22]中提出的基于离散时间降阶广义比例积分观测器(discrete time reduced order generalized proportional integral observer,RGPIO)的电机预测调速算法,更符合实际应用.

相较于扰动观测器,等价输入干扰(equivalent input disturbance,EID)方法不需要系统的逆模型,因此避免了不稳定极点和零点之间的对消,而且还不要求掌握外部干扰的信息[23].该方法已被成功应用到线性系统[24-25]、时延系统[26-27]和非线性系统[28]中.相比传统EID结构中的龙伯格观测器,滑模观测器(sliding mode observer,SMO)不仅将系统和观测器输出之间的误差线性反馈,而且还能够根据观测误差产生滑模运动,从而实现对状态变量快速、精确地估计[29].

本文针对不确定性和外部干扰引起的磁悬浮球系统控制性能下降的问题,提出了一种基于等价输入干扰滑模观测器的模型预测控制(MPC+EIDSMO)方法.该方法首先将系统不确定性和外部干扰转化为一个施加在控制输入端的等价输入干扰,然后采用等价输入干扰滑模观测器对系统状态变量及等价输入干扰进行估计.最后基于状态估计值设计模型预测控制器,并将等价输入干扰估计值以前馈的方式补偿后得到最终的复合控制律.仿真和实验结果表明,相较于基于EID观测器的模型预测控制方法和基于龙伯格观测器的积分模型预测控制方法,所提方法提高了磁悬浮球系统的跟踪性能并且有效抑制了系统不确定性和外部干扰.

2 磁悬浮球系统的数学模型

本文所采用的磁悬浮球控制系统结构如图1所示,该系统主要由电磁线圈、功率放大器、控制器、激光位置传感器、钢球和上位机组成.作为一种研究磁悬浮技术的实验平台,其基本原理是通过调节电磁线圈中的电流来改变电磁力,以使钢球稳定在固定位置或驱动钢球跟踪上参考位置轨迹.需要注意的是,该实验平台为单自由度磁悬浮系统,即钢球只能够在垂直方向上运动,而不会受到其它方向上的力的作用.

根据文献[7],磁悬浮球系统数学模型可以表示为

其中:m为钢球质量,g为重力加速度,h为电磁铁表面与钢球之间的间隙,i为通过电磁线圈的瞬时电流,F(i,h)为电磁力,u(t)为施加到电磁线圈上的控制电压,R为电磁线圈的等效电阻,LR为电磁线圈的自感,KR为电磁线圈的互感,µ0为真空磁导率,S为电磁铁磁导截面积,N为线圈匝数.

由式(1)可知,F(i,h)与i,h之间是非线性的关系.为了便于下文中控制器的设计,对电磁力F(i,h)在平衡点(i0,h0)进行泰勒级数展开如下:

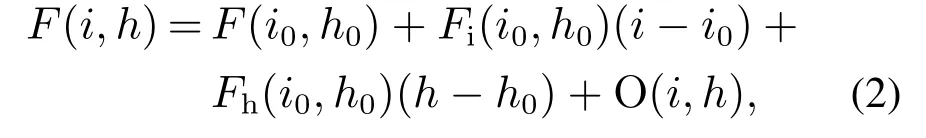
其中:

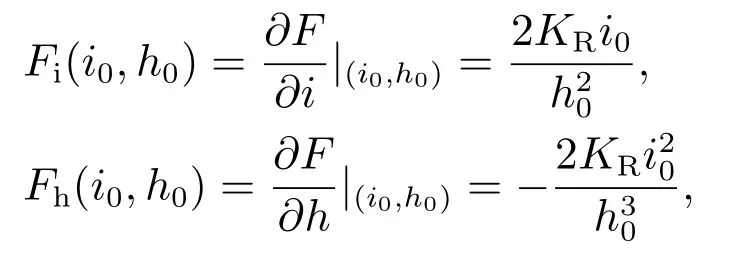
O(i,h)是F(i,h)泰勒展开式的高阶项,且F(i0,h0)=mg.

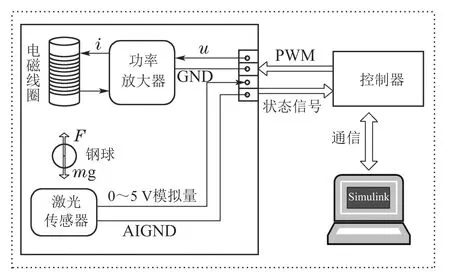
图1 磁悬浮球控制系统结构Fig.1 Structure of the magnetic levitation ball control system

把式(2)代入式(1)中的第1个等式可得

令电压信号为系统的输入,并且考虑磁悬浮球系统受到外部干扰ω(t)的影响,那么

y为测量输出,d(t)=d˜(t)+(a−a0)x1+(b−b0)u为总扰动,包括了未建模动态,参数不确定性和外部干扰,a0和b0分别表示a和b的标称值.因为b00,易知磁悬浮球系统是可控和可观测的,且在虚轴上无零点.

此外,给定位置参考信号表示为yc(t),位置跟踪误差定义为e(t)=y(t)−yc(t).下一节将要设计控制器,使误差状态在系统不确定性和外部干扰存在的情况下渐进收敛到零,即随着t →∞,e(t)→0.

3 控制器设计

本节中提出了一种基于等价输入干扰滑模观测器的模型预测控制(MPC+EIDSMO)方法(图2).

图2 基于等价输入干扰滑模观测器的模型预测控制框图Fig.2 Block diagram of EIDSMO-based MPC

该方法首先将系统不确定性和外部干扰转化为一个施加在控制输入端的等价输入干扰,然后采用等价输入干扰滑模观测器对系统状态变量及等价输入干扰进行估计.最后基于状态估计值设计模型预测控制器,并将等价输入干扰估计值以前馈的方式补偿后得到最终的复合控制律.

3.1 等价输入干扰滑模观测器的设计

根据文献[24]对EID的定义,将原系统受到的总扰动转化为一个施加在控制输入通道上的等价输入干扰de(t),则原系统(5)对应的EID系统可以描述为

由于引入了EID,系统的状态变量发生了改变,因此需要采用等价输入干扰滑模观测器对EID系统其状态变量及等价输入干扰予以观测估计.选择系统输出和观测器输出之间的观测误差的反正切函数作为滑模控制律,以有效地抑制抖动,同时还能够产生连续的观测器输入.对于EID系统(6)设计滑模观测器[30]

3.2 连续时间模型预测控制

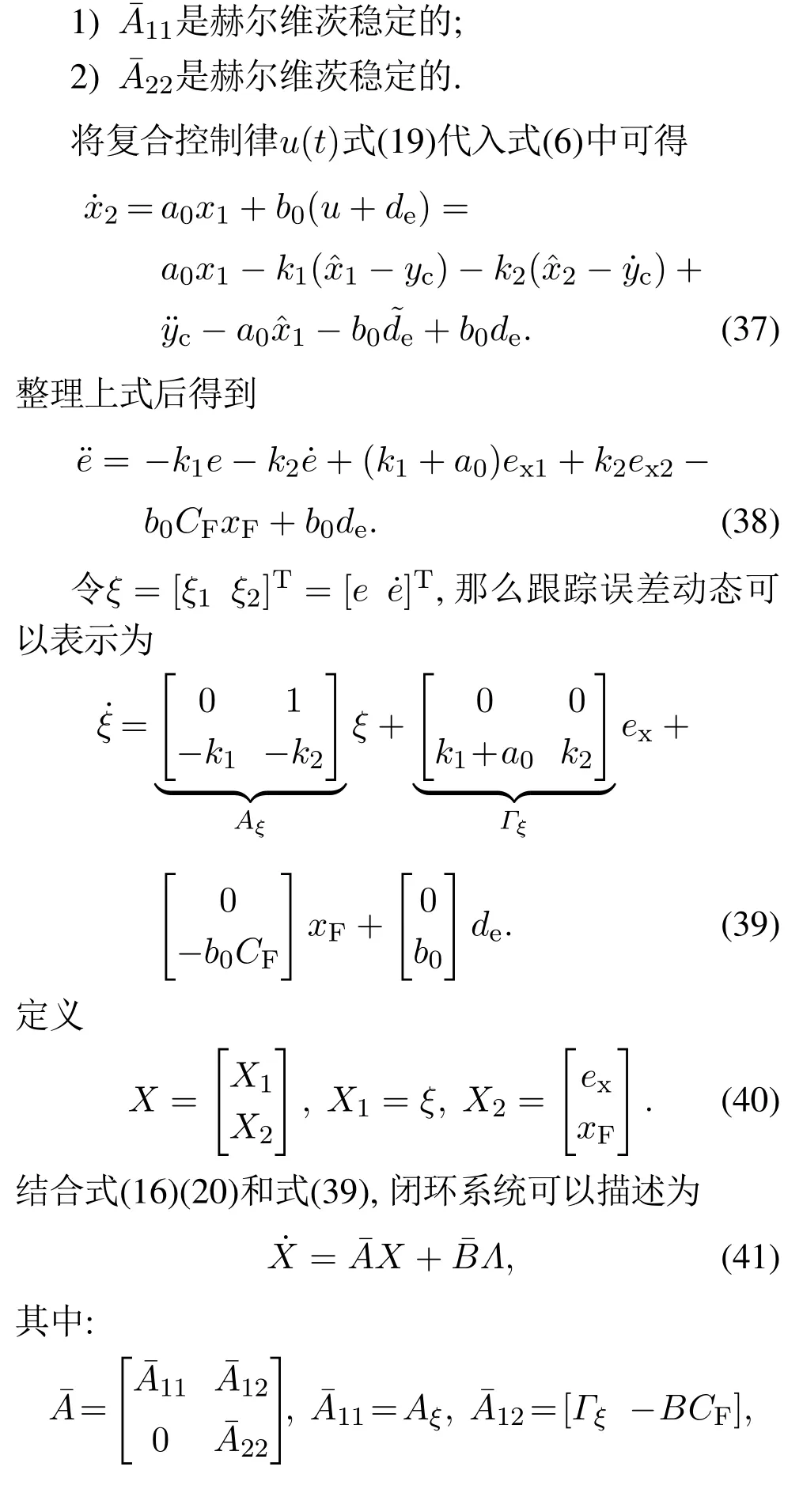
3.3 闭环系统稳定性分析

全局一致毕竟有界的概念[33]和引理1[30]将被用于闭环系统稳定性的分析.

引理1如果是赫尔维茨稳定的,那么闭环系统系统是全局一致毕竟有界的.即

4 仿真和实验验证

采用MATLAB/Simulink对磁悬浮球系统和所提控制方法进行数值仿真和实验验证,其中磁悬浮球系统各参数如表1所示.

表1 磁悬浮球系统参数Table 1 Parameters of the magnetic levitation ball system

由表1中的参数标称值可以计算出系统模型(5)中的a0=61,b0=−0.3,为了模拟系统受到参数不确定性的影响,仿真和实验中选取a0=58,b0=−0.28.为了更好的验证本文所提出的MPC+EIDSMO方法的跟踪性能和抗扰动性能,将其与基于传统EID观测器的模型预测控制(MPC+EIDO)方法以及基于龙伯格状态观测器的积分模型预测控制(IMPC+LO)[18]方法进行比较.最后,仿真和实验结果将采用时间乘绝对误差积分准则(integral of time multiplied by the absolute value of error,ITAE)和均方根误差(root mean square error,RMSE)[8]两项指标来定量分析.仿真和实验采样周期均为0.001 s.

其中:yc为给定位置信号,y为系统输出.

4.1 数值仿真

MPC+EIDSMO方法参数:预测时域Tp=0.04 s,观测器增益L=[1200 9000]T,滑模增益Ks=60,取扰动的最高频率ωr=0.5π,则低通滤波器参数选为AF=−10,BF=10,CF=1.MPC+EIDO方 法参数:Tp=0.04 s,观测器增益L=[1200 9000]T,低通滤波器参数选为AF=−10,BF=10,CF=1.IMPC+LO方法参数:预测步长Np=30,控制步长Nc=2,观测器增益L=[1200 9000]T.

正弦跟踪和方波跟踪仿真结果分别如图3-4所示.其中“Set Position”表示参考位置.表2为3种方法的跟踪性能定量分析结果,可以看到在仿真时将参数调到各自最佳的情况下,3种方法都能实现对给定轨迹的跟踪.值得注意的是,在跟踪方波信号时,由于在一些特定时刻跟踪信号的突变,导致了对应时刻控制输入的变化较大.进一步验证抗扰动性能,分别在平衡位置时加入幅值为1 V,周期为4 s的正弦波扰动和幅值为1 V,周期为2 s的锯齿波扰动,仿真结果如图5-6所示,表3为3种方法的抗扰动性能定量分析结果,相较之下,MPC+EIDSMO方法具有更好的抗扰动性能.

图3 3种控制器作用下的正弦跟踪响应曲线(仿真)Fig.3 Response curves of sine wave tracking under three controllers(simulation)

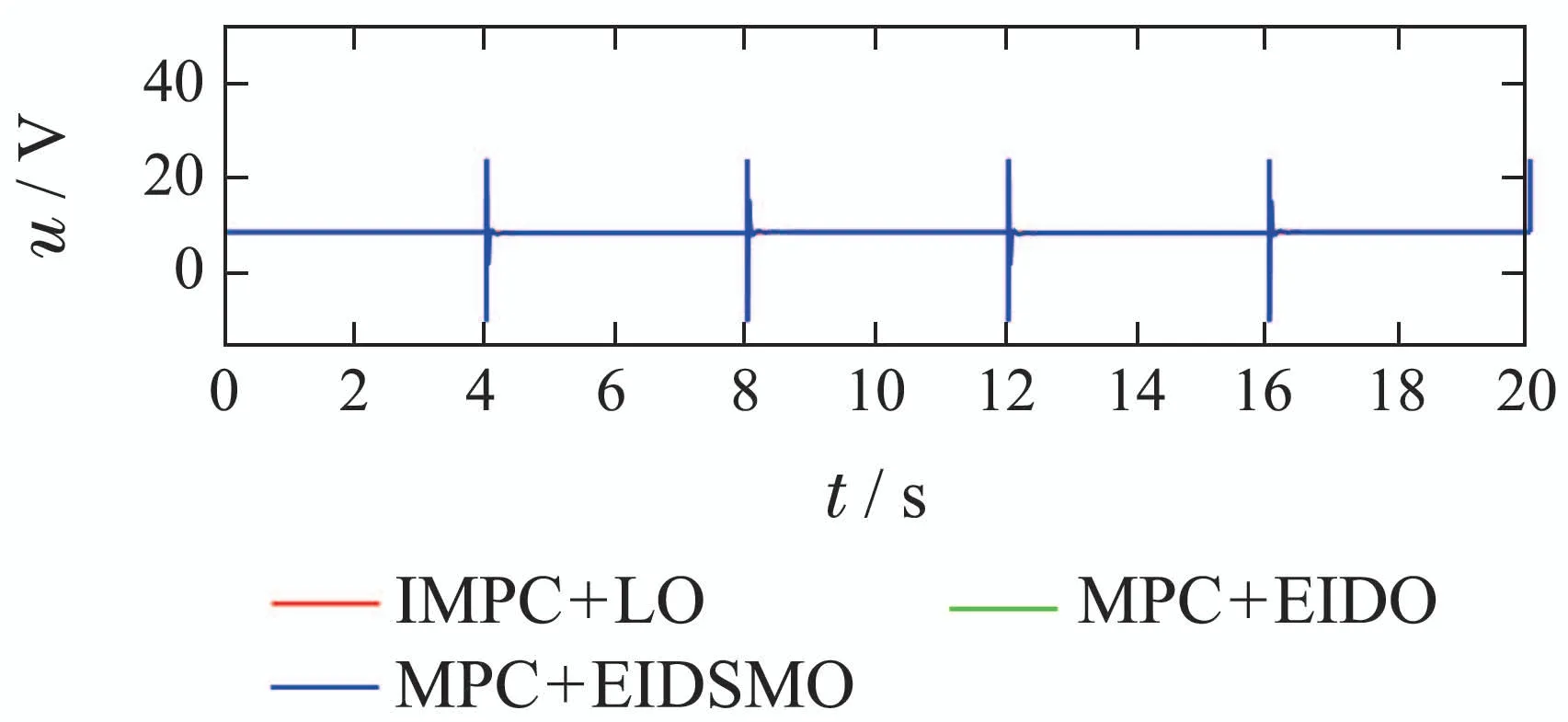
图4 3种控制器作用下的方波跟踪响应曲线(仿真)Fig.4 Response curves of square wave tracking under three controllers(simulation)

表2 位置跟踪的性能指标比较(仿真)Table 2 Comparison of performance indexes for position tracking(simulation)

图5 3种控制器作用下的正弦扰动响应曲线(仿真)Fig.5 Response curves of sine wave disturbance under three controllers(simulation)

图6 3种控制器作用下的锯齿波扰动响应曲线(仿真)Fig.6 Response curves of sawtooth wave disturbance under three controllers(simulation)

表3 扰动抑制的性能指标比较(仿真)Table 3 Comparison of performance indexes for disturbance suppression(simulation)

4.2 实验结果

磁悬浮球系统实验平台如图7所示.其中硬件控制器由Raspberry Pi和STM32组成,主要用于收集传感器数据和计算控制信号,激光位置传感器用于采集位置信息,励磁线圈用于产生驱动小球在垂直方向上运动的力.实验中的控制算法由MATLAB/Simulink软件实现.

图7 磁悬浮球系统实验平台Fig.7 Experimental platform of the magnetic levitation ball system

MPC+EIDSMO方法参数:预测时域Tp=0.1 s,观测器增益L=[1200 10000]T,滑模增益Ks=40,取扰动的最高频率ωr=0.5π,则低通滤波器e参数选为AF=−10,BF=10,CF=1.MPC+EIDO方法参数:Tp=0.1 s,观测器增益L=[1200 10000]T,低通滤波器参数选为AF=−10,BF=10,CF=1.IMPC+OB方法参数:预测步长Np=15,控制步长Nc=2,观测器增益L=[1200 10000]T.

正弦跟踪和方波跟踪实验结果分别如图8-9所示,表4为3种方法的跟踪性能定量分析结果,可以看出MPC+EIDSMO方法较其它两种方法具有更快的收敛速度和更小的超调量,且ITAE和RMSE两项性能指标也有所提升.

图8 3种控制器作用下的正弦跟踪响应曲线(实验)Fig.8 Response curves of sine wave tracking under three controllers(experiment)

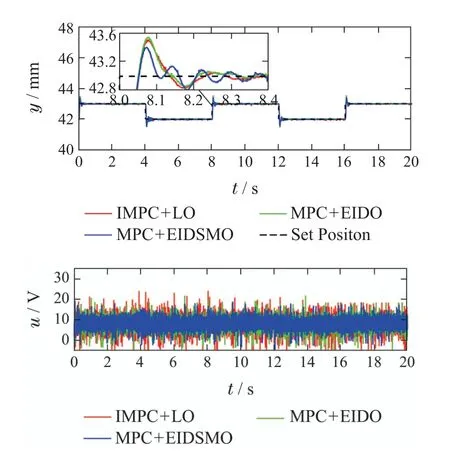
图9 3种控制器作用下的方波跟踪响应曲线(实验)Fig.9 Response curves of square wave tracking under three controllers(experiment)

表4 位置跟踪的性能指标比较(实验)Table 4 Comparison of performance indexes for position tracking(experiment)

进一步验证抗干扰性能,分别在平衡位置时加入幅值为1 V,周期为4 s的正弦波扰动和幅值为1 V,周期为2 s的锯齿波扰动,实验结果如图10-11所示,表5为3种方法的抗扰动性能定量分析结果,相较之下,MPC+EIDSMO方法具有更好的抗扰动性能.值得注意的是,实验部分的控制输入同仿真相比具有较大的噪声,这主要是由于激光位置传感器测量和功率变换器开关特性引起的,在仿真中则不存在.

图10 3种控制器作用下的正弦扰动响应曲线(实验)Fig.10 Response curves of sine disturbance under three controllers(experiment)

图11 3种控制器作用下的锯齿波扰动响应曲线(实验)Fig.11 Response curves of sawtooth disturbance under three controllers(experiment)

表5 扰动抑制的性能指标比较(实验)Table 5 Comparison of performance indexes for disturbance suppression(experiment)

5 结论

本文研究了在扰动影响下的磁悬浮球系统位置跟踪问题.为了在不牺牲系统标称控制性能的前提下提高闭环系统的抗干扰性能,提出了一种基于等价输入干扰滑模观测器的模型预测控制方法.通过等价输入干扰滑模观测器得到等价输入干扰的估计值,将其与模型预测控制最优控制律相结合得到最终的复合控制律,实现了磁悬浮球系统在扰动存在下的位置跟踪控制.仿真和实验结果表明,与内含龙伯格观测器的传统EID观测器相比,等价输入干扰滑模观测器具有更快的收敛速度.相较于经典的积分模型预测控制方法,基于等价输入干扰滑模观测器的模型预测控制方法对扰动具有更好的抑制效果.