传输时延环境下信息物理融合系统中恶意病毒传播的稳定性与分岔分析

王 璐,肖 敏,周 帅,张跃中

(南京邮电大学自动化学院,江苏南京 210023)

1 引言

计算机技术、通信技术和嵌入式技术的发展,极大丰富和便利了人类的生活.由于低功耗、高容量、小尺寸计算设备的出现,无线通信技术的不断革命,丰富的互联网带宽资源持续涌现,以及低成本、高性能的硬件产品不断优化等大环境的影响,人们对计算资源和物理资源的需求已由扩充系统功能转化为资源的合理整合利用与调度优化,并且希望所提供的网络信息服务更安全、灵活和智能.在此类需求的刺激下,促进了信息物理融合系统(cyber-physical systems,CPS)的产生.类似互联网改变了人与人之间的交互方式一样,CPS的出现将会改变人类与周围物理世界之间的交互和控制方式[1].CPS是一种综合计算,通信和物理环境的新型智能系统[2],通过嵌入计算、通信和控制技术到物理环境所有类型的物体结构中,将计算资源和物理资源进行有机融合与深度协作,实现大规模物理系统的实时感知、信息服务和动态控制,从而产生巨大的社会影响和经济效益.2006年美国国家自然基金委员会首次提出CPS的概念.2007 年,CPS居美国信息技术领域八大重要信息技术研发之首.由于信息技术的高速发展,CPS在医疗设备、航空航天系统、交通运输、智能电网、国防系统、机器人系统、自动控制系统、建筑和环境控制以及智能空间等众多领域应用越来越广泛[3-6],成为建设人类未来智慧城市的基础,引起了世界各国、学术领域和商业界的关注和重视[7-9].

国家电网、核电站、铁路、空中交通管制、水/污水基础设施、银行系统等关键的基础设施均属于CPS,因此确保其安全性和可信性是推动CPS进一步发展的首要问题.但CPS的生存环境十分复杂,并且容易受到很多因素的干扰、侵袭或者遭受恶意病毒的攻击[10-11],以至于时常会产生无法满足人们预期要求的情形,从而引发系统故障或造成系统失调,最终导致众多CPS应用领域遭受严重损失[12-14],给国家基础设施和人民群众的生命财产安全带来巨大的威胁.例如,2010年6月首次检测出来的“震网”病毒[15],是首个专门定向攻击物理世界中基础能源设施的恶意病毒.当时伊朗境内的核工厂与诸多工业企业昂贵的控制系统出现意外,都是因为受“震网”的攻击所致.随着现代科学技术的不断发展,越来越多的人开始研究病毒技术,病毒的数量、被攻击的平台数以及病毒的复杂性和多样性都开始显著提高.现代病毒不仅更为智能,且其攻击机制也更为复杂,这预示着恶意病毒使用的技术将开启一个新的时代,CPS面临着严峻的危机与挑战[16-17].因此,为提高CPS的安全性和可靠性,必须首先明确恶意病毒在CPS中的传播机理和动力学行为.

由于系统各节点之间病毒信号的传输需要一定的时间,一切感染攻击系统的行为都是随着时间的变化而发生演化,因此恶意病毒的传播是一个逐步实现对系统进行破坏的动态过程[18].在这个动态过程中,由于人为因素对系统的防御保护,以及系统物理组件的电容,有限的阻抗等客观因素的存在,会让病毒信号的传输产生延迟,因此恶意病毒在CPS的传播过程中出现时滞的现象是不可避免的[19-22].一般情况下,时滞对系统的稳定性有干扰和破坏作用[23-25],会导致系统平衡点失去稳定,产生非常复杂的分岔、混沌等动力学行为[26-28],这对于CPS的可信性[29]会产生非常恶劣的影响.

CPS与人类的生活和社会的发展密切相连,在国防系统、国家电网、航天系统等关键CPS中,分岔、混沌等不利的动力学行为会引发电压震荡、信息拥塞等故障,这会严重影响CPS的可信性,所以研究带有时滞的恶意病毒在CPS中的传播机理是十分必要且重要的.但在传统CPS恶意病毒传播模型的研究中,并没有考虑到时滞对系统的影响[30],因此传统模型不能准确刻画出恶意病毒在CPS中真实的传播过程.为提高系统的正确性和可靠性,对CPS中带有时滞的恶意病毒传播模型进行描述、分析和验证,从而有效提高系统的正确性、安全性、可用性和可靠性等可信属性,这对于建设和发展高可信的CPS具有重要意义.

CPS将离散而强大的计算逻辑与物理和工程系统结合在一起,以监视和控制物理和工程系统的连续动态.而恶意病毒的传播会致使CPS出现叉型、鞍结点、Neimark-Sacker、Hopf等多种分岔现象.通过非线性动力学理论研究恶意病毒在CPS传播过程中的动力学行为,对于掌握恶意病毒的内在特性具有重要意义.其中,Hopf分岔是一种常见的动态分岔现象[31-34].目前,在Hopf 分岔研究方面,已获得了许多重要成果[35-39].对Hopf分岔的研究不仅有助于理解恶意病毒在CPS传播过程中的数学理论依据和背景,而且为预防恶意病毒在CPS中的传播可以提供可能的途径.因此研究带有时滞的恶意病毒在CPS中的传播机理和分岔现象具有重要的理论意义和实际价值.

综上所述,在传输时延环境下,针对信息物理融合系统提出了一类具有时滞的恶意病毒传播模型,并研究了该类系统的动力学特性.本文的主要贡献如下:

1) 考虑到时滞不可被忽略的现实客观因素,并结合恶意病毒在信息物理融合系统中的传播特点,本文提出一类更具一般性的时滞恶意病毒传播模型.

2) 选取时滞作为分岔参数,研究了时滞对系统局部稳定性和Hopf分岔的影响.

3) 讨论了模型参数对恶意病毒传播过程的影响,发现分岔点τ0与感染率a成反比,与预防效果系数p成正比.

2 模型描述

当CPS被某一类恶意病毒攻击时,CPS并不会立刻沦陷,恶意病毒在CPS中的每个节点状态传播时均需要一定的时间.设初始时刻CPS中含有可以被恶意病毒操纵的漏洞节点,可称该漏洞节点为易感染节点(susceptible node);经过一定时间后,恶意病毒被激活后开始进行猛烈地主动攻击,易感染节点被吞噬转化为感染节点(infectious node);当恶意病毒的破坏作用被用户察觉后,用户将进行杀毒治愈措施修复系统,感染恶意病毒较轻的节点直接被治愈,转化为恢复节点(recovered node);恶意病毒吞噬严重的节点被隔离,转化为隔离节点(quarantine node),该节点经过修复治愈后转化为恢复节点;恢复节点经过一段时间后丧失免疫功能又重新转化为新的易感节点.上述4种节点分别简称为S态节点、I态节点、R态节点以及Q态节点.各状态节点转化流程如图1所示,其中:

1) 所有新接入的节点均视为S态节点.

2) 为防御恶意病毒的攻击,用户会对S态节点采用一定的防御行为,所以S态节点会经过一定的潜伏期τ1后才会转化为I态节点.此类防御行为的成效与被感染率成反比,因此设被感染率为,其中a是感染率,p是预防效果系数.

3) 感染较轻的I态节点以治愈率b经过一定的治愈期τ2被修复为R态节点,感染严重的I态节点会以隔离率c经过一定的隔离期τ4转换为Q态节点,再以治愈率d经过一定的治愈期τ5被修复为R态节点.

4)R态节点经过一定的免疫期τ3后失去免疫能力转化为S态节点,其转化率为q.

5) 当CPS稳定运行时,系统中的各节点处于动态平衡状态,即新接入系统的节点数目与退出系统的节点数目基本一致,接入率v与退出率u相等.

6) 接入率v、退出率u、预防效果系数p、感染率a、隔离率c、治愈率b与d、转化率q均为非负数.

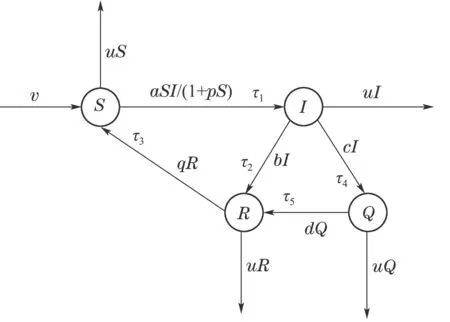
图1 SIQR模型节点转化示意图Fig.1 Node transformation in SIQR

由于CPS是一个具有动态性、自适应性等特性的分布式复杂系统,其系统行为很难预测.并且以往恶意病毒的传播模型不能准确刻画恶意病毒在CPS中的实际传播过程,因此许多研究者考虑到CPS的动态性和自适应性等特点,结合节点隔离机制与链路重连机制逐步建立了很多恶意病毒在CPS中的传播动力学模型[30,40].在文献[30]中,作者考虑到CPS 节点动态接入和退出等特征,进一步发展完善了CPS 中恶意病毒的传播模型,即易感-感染-隔离-治愈(susceptibleinfected-quarantined-recovered,SIQR)模 型.众 所 周知,时滞是不可避免的,然而文献[30]忽略了恶意病毒在传播过程中的时滞因素.如文献[24-27]所述,有必要将时滞纳入动力系统,以便依据时滞反映系统的动力学行为.因此,基于文献[30]中的SIQR模型,本文考虑具有时滞的系统

注1在以往CPS恶意病毒传播模型的研究中[30],并没有考虑到时滞对系统的影响.但恶意病毒在CPS的传播过程中出现时滞的现象是不可避免的,因此传统模型[30]并不能准确刻画出恶意病毒在CPS中真实的传播过程.本文为提高系统的正确性和可靠性,在文献[30]的基础上将时滞因素纳入动力系统,以便依据时滞反映系统的动力学行为.

注2值得注意的是,S态节点会经过潜伏期τ1后才会转化为I态节点,I态节点要经过隔离期τ4后才会转换为Q态节点,I态节点和Q态节点均分别需要经过相应的治愈期τ2和τ5后才会被修复为R态节点,同样R态节点在经过一定的免疫期τ3后失去免疫能力转化为S态节点.显然,时滞对各态节点均有滞后影响.但传统CPS恶意病毒传播模型研究[30,40]忽略了各节点状态转变必然存在的时间延迟.如文献[41-42]所述,有必要将时滞纳入动力系统,以便根据系统的真实过程来反映系统的动力学行为.因此本文提出了一类带有时滞的恶意病毒传播模型,更具有一般性.

3 局部稳定性和Hopf分岔分析

为了研究带有时滞的恶意病毒在CPS中的传播机理,需要对所建动力学模型进行稳定性和Hopf分岔分析,从而为消除或延迟恶意病毒传播过程中引发的不利分岔行为提供理论依据.

令系统(1)中的方程右端等于0,可知系统(1)恒有平衡点O∗=(S∗,I∗,Q∗,R∗).将系统(1)在平衡点O∗=(S∗,I∗,Q∗,R∗)处线性化,得

考虑到CPS的工程意义,恶意病毒在CPS中的传播行为,可以看做是一个攻击与防守治愈的对抗过程.攻击阶段为S态节点转化成I态节点的过程,防守治愈阶段为I态节点转化成S态节点的过程.这两个过程在当今时代同等技术手段下花费的时间相近.由图1可知,防守治愈阶段有两条路径,每条路径上耗费的时间基本相似.因此,假设τ1=τ2+τ3=τ3+τ4+τ5=τ.特征方程(3)化为

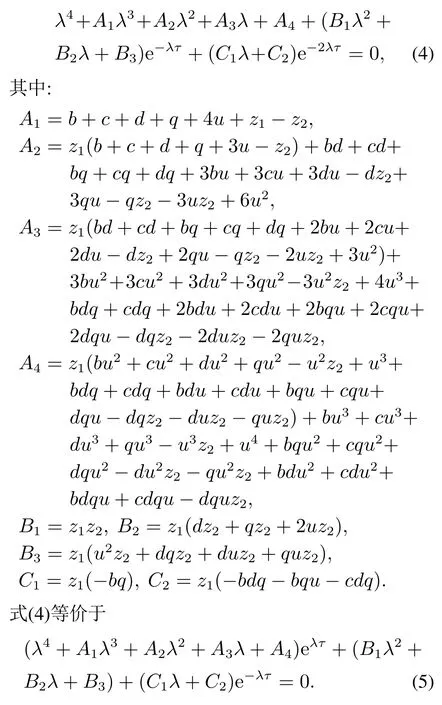
注3多时滞的出现增加了特征方程中超越项的复杂性,使动力学分析复杂化.因此,目前大多数的文献[43-45]都对时滞作了相应的假设,以简化动力学的理论分析.例如,文献[43]中假设传输时滞和反馈时滞的总和是一个组合参数.在文献[44]中,假定不同层中同一位置神经元的时滞之和相等.文献[45]采用了这样的假设,即猎物的反馈时滞与成熟捕食者怀孕所产生的时滞相等.因此,在本文中假设攻击与防守治愈花费的时间相等来简化特征方程.

3.1 无时滞的情形τ=0

当τ=0时,式(5)转化为

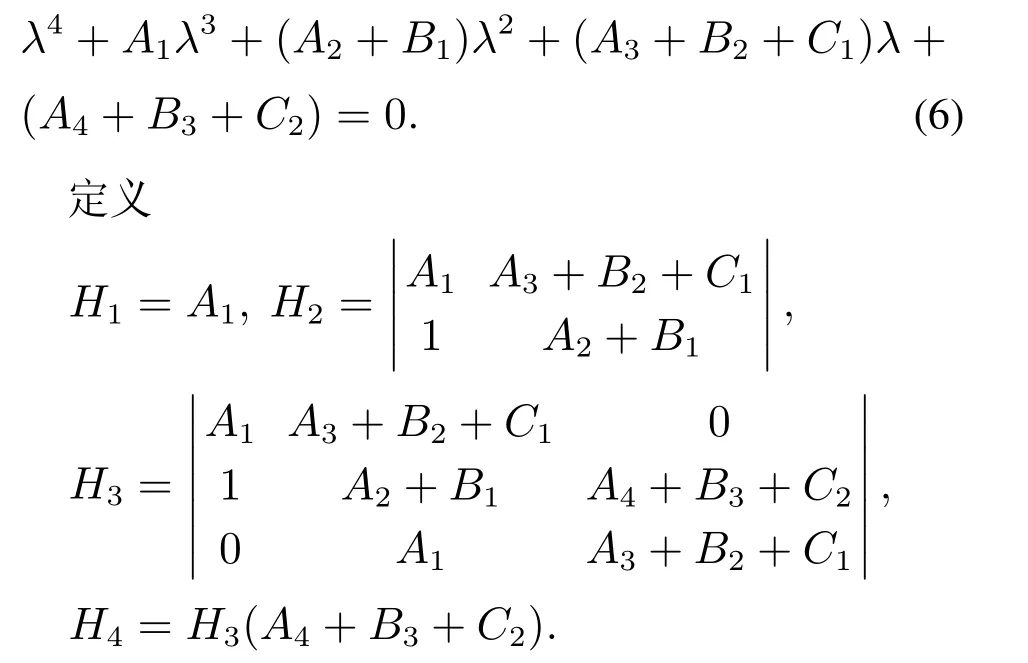
根据Routh-Hurwitz判据,可得到以下引理.

引理1当τ=0时,如果Hi >0(i=1,2,3,4),则系统(1)在平衡点O∗=(S∗,I∗,Q∗,R∗)附近是局部渐近稳定的.

3.2 含有时滞的情形τ0

3.3 验证穿越条件

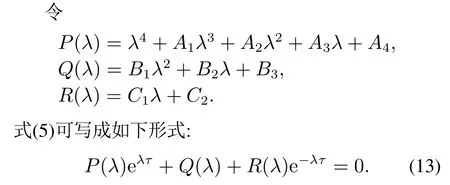
从而可以得到如下引理:

引理3如果M1M3+M2M4>0,则>0.

根据上述引理1−3,可得到下列定理:

定理1i) 当τ=0时,如果Hi>0(i=1,2,3,4),则系统(1)在平衡点O∗=(S∗,I∗,Q∗,R∗)附近是渐近稳定的;

ii) 如果Dσ >0(σ=1,2,···,7)且D8<0,那么当τ ∈[0,τ0)时,系统(1)在平衡点O∗=(S∗,I∗,Q∗,R∗)附近是渐近稳定的;当τ >τ0时,系统(1)处于不稳定状态;

iii) 如果ii)中所述的条件成立,则当τ穿过τ0时,系统(1)在平衡点O∗=(S∗,I∗,Q∗,R∗)处产生Hopf分岔,其中τ0是最小的临界点.

4 数值仿真

为了验证上述理论分析的正确性,采用一个具体的数值仿真示例来研究带有时滞的恶意病毒在CPS中的稳定性和分岔动力学.选取文献[30]中相同的一组参数值,即a=0.35,b=0.08,c=0.1,d=0.1,u=0.05,v=0.05,p=0.1,q=0.15,选择时滞τ作为分岔参数,可得到系统(1)的如下示例:

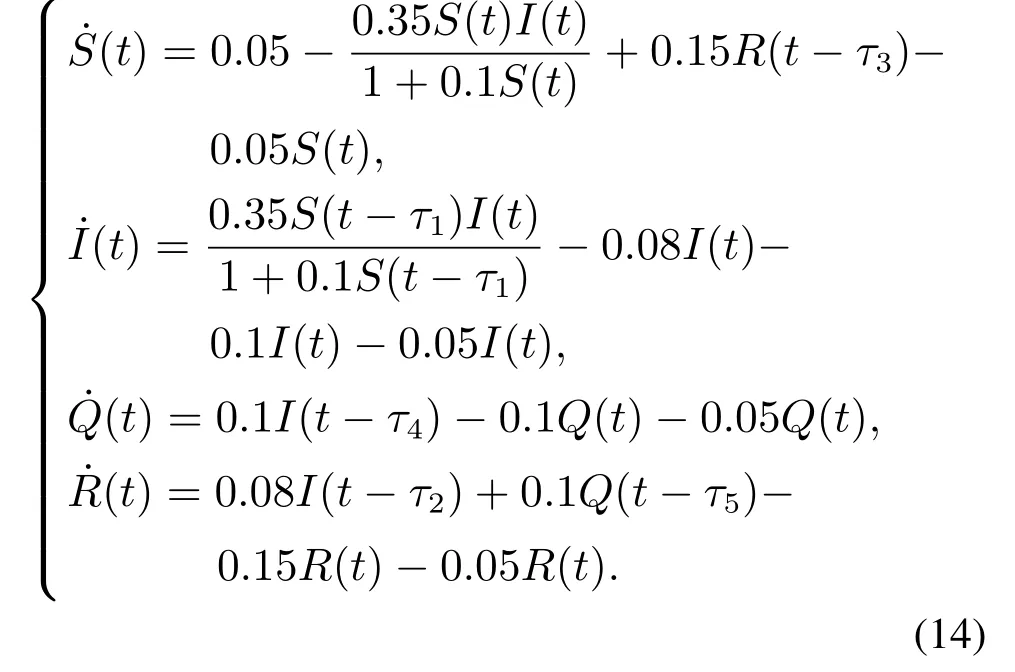
通过计算,系统(14)的唯一平衡点为O∗=(0.703,0.124,0.082,0.091),并得到ω0=0.08,τ0=14.08.

图2(a)表明,当τ=13.5<τ0时,各态节点曲线最终均收敛成一条直线,表明系统(14)在平衡点O∗附近是渐近稳定的.相反,图3(a)表明,当τ=14.11>τ0时,各态节点曲线发生震荡,表明系统(14)变得不稳定,在平衡点O∗附近产生Hopf分岔.

从相图来看,图2和图3中的(b)(c)(d)为S(t),I(t),Q(t),R(t)之间的相位关系图.相位图也清晰地表明当τ=13.5<τ0时,曲线收敛到一个极限点,即平衡点O∗,如图2(b)(c)(d)所示.相反,当τ=14.11>τ0时,曲线产生一个极限环,这意味着Hopf分岔的发生,如图3(b)(c)(d)所示.

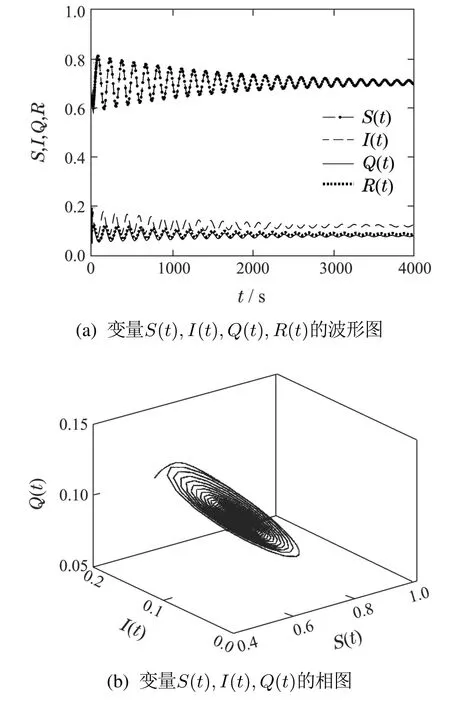
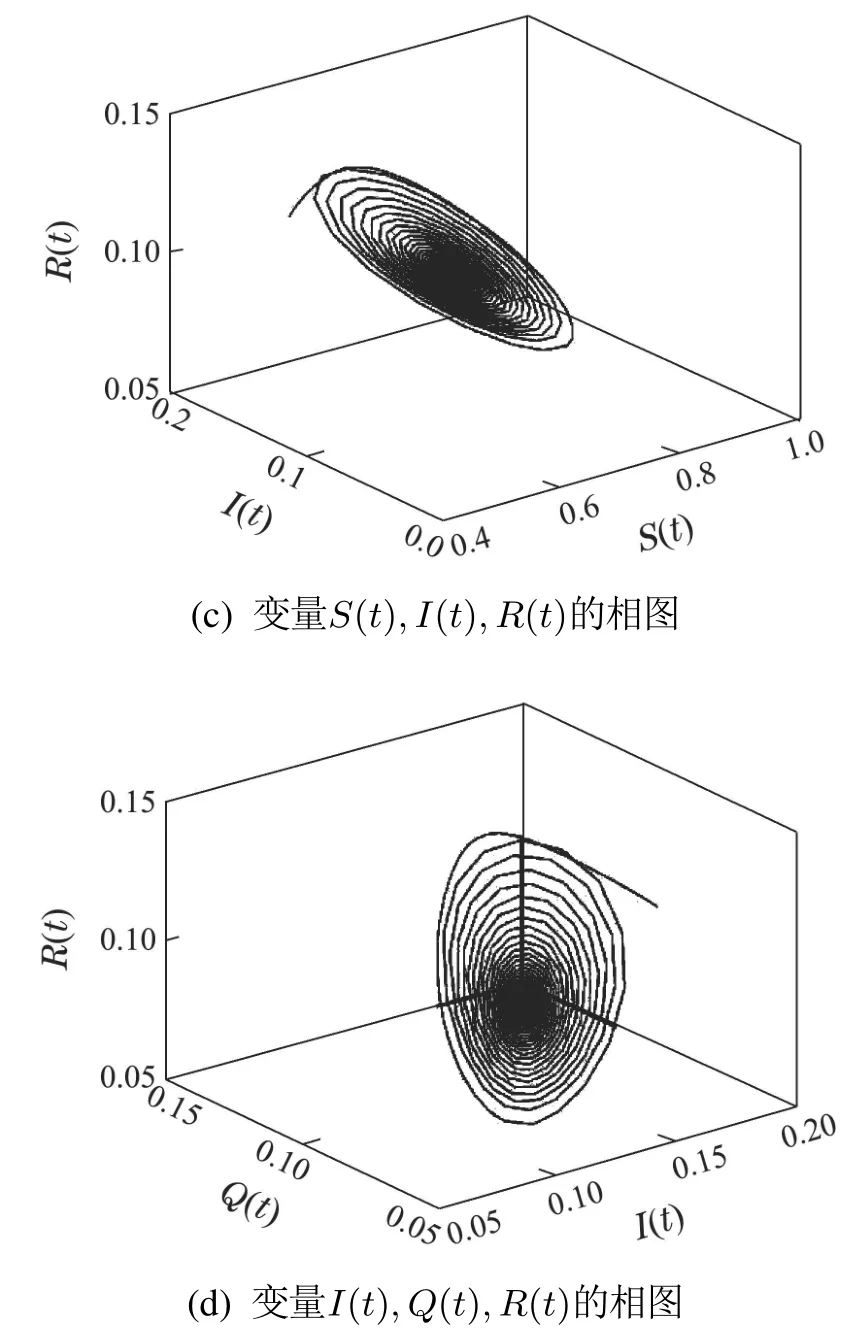
图2 当τ=13.5<τ0=14.08时,系统(14)的波形图与相位图Fig.2 Waveform and phase diagram of system(14)when τ=13.5<τ0=14.08

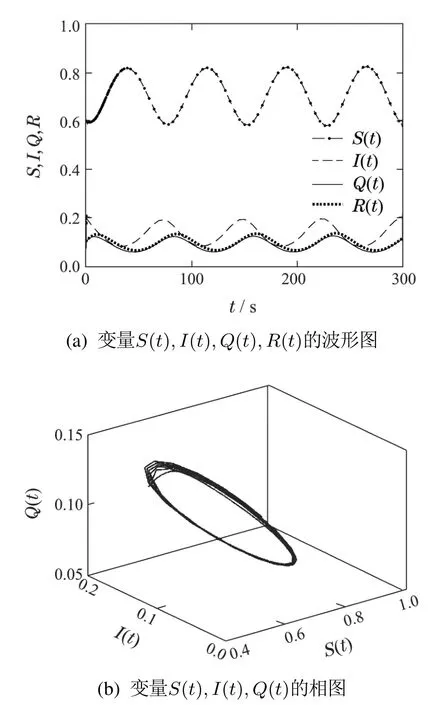
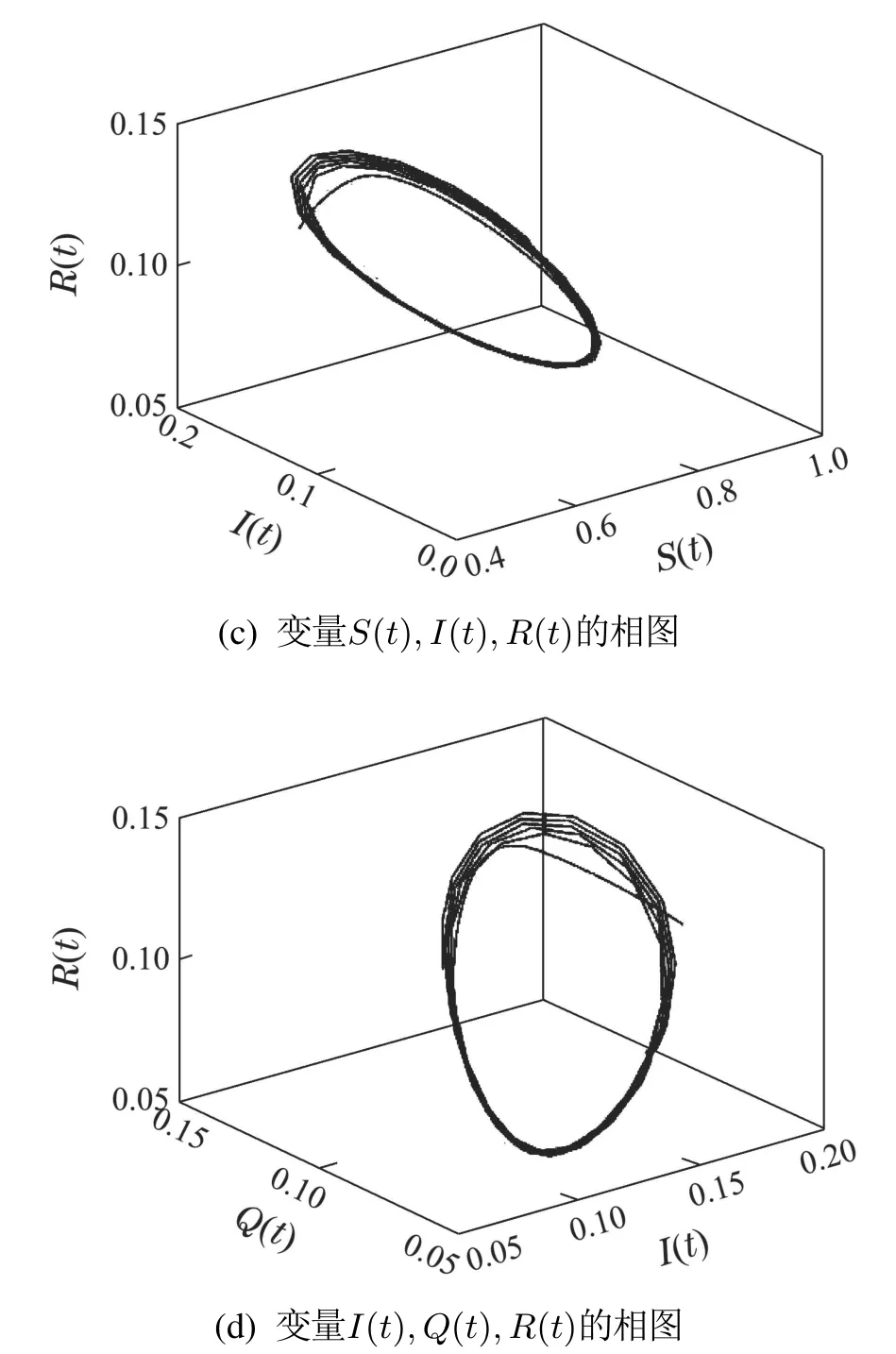
图3 当τ=14.11>τ0=14.08时,系统(14)的波形图与相位图Fig.3 Waveform and phase diagram of system(14)when τ=14.11>τ0=14.08

本文进一步研究了模型参数对恶意病毒传播过程的影响,图4表明,分岔点τ0与感染率a成反比,与预防效果系数p成正比.

显而易见,当感染率a增大时,分岔点τ0减小,即稳定阈值变小,系统的稳定性变差.反之,当预防效果系数p增大时,分岔点τ0也增大,即稳定阈值扩大,稳定性增强,此时系统不易被病毒入侵.

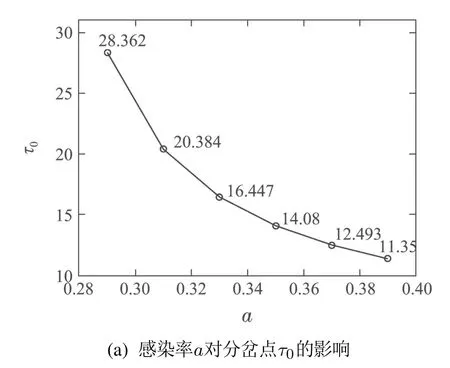
图4 系统参数a=ak,p=pk(k=1,2,···,6)时,感染率a和预防效果系数p对系统(14)分岔点τ0的影响Fig.4 The influences of parameters a=ak,p=pk(k=1,2,···,6)on the bifurcation point τ0 for system(14)

注4本文数值仿真选取文献[30]中相同的系统参数.当τ=0时,系统(14)退化为文献[30]中的无时滞系统,此时系统是稳定的.当τ=8.1时,由图5(a)可知系统(14)仍处于稳定状态.但当τ=18.36时,由图5(b)可知系统(14)发生Hopf分岔,失去稳定性.由此可知,当τ取值较小时,系统仍能保持稳定,但当τ值增大并超过阈值τ0时,系统的稳定性遭到破坏.因此研究信息物理融合系统中的病毒传播动力学,充分考虑时滞因素是十分必要的.

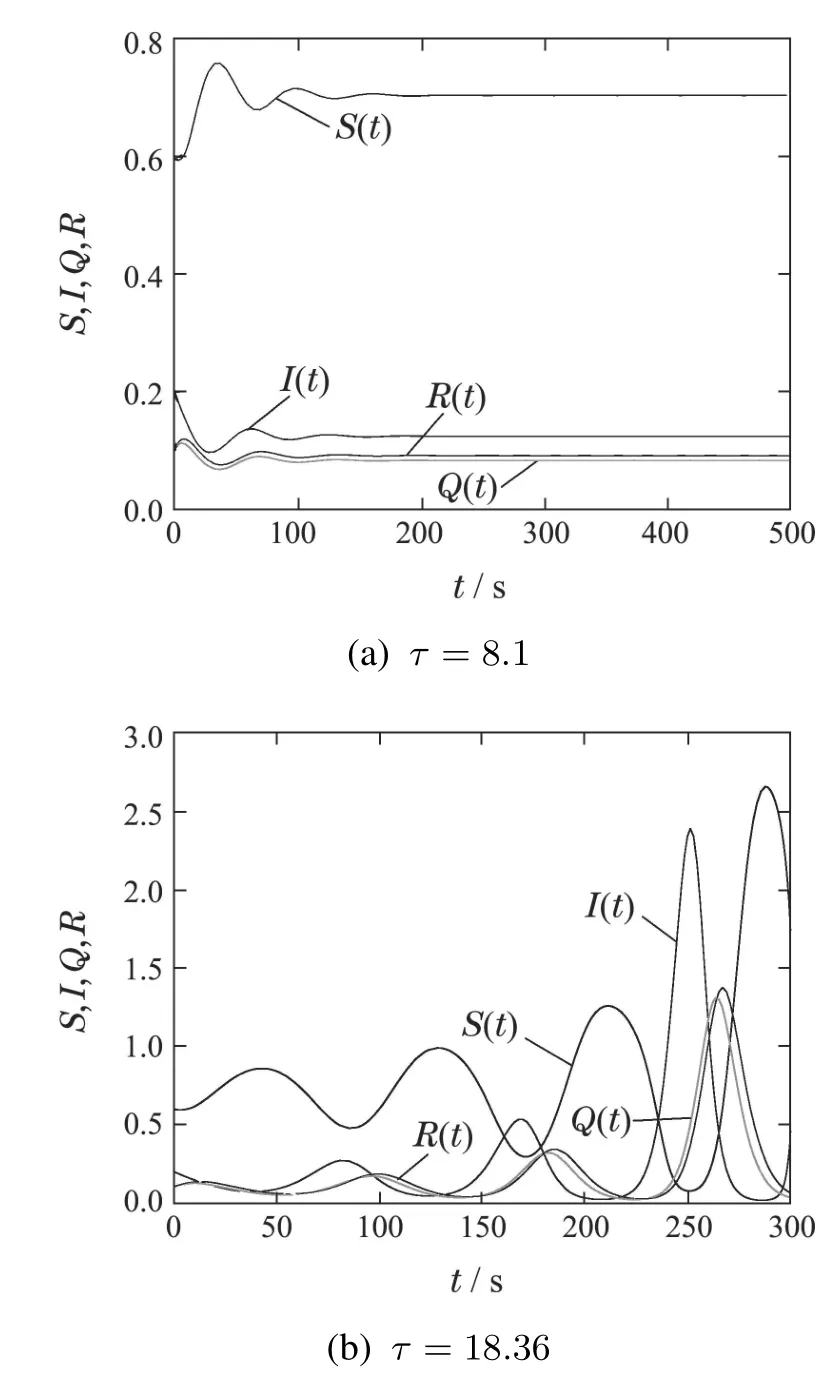
图5 当τ为不同的数值时,系统(14)的波形图Fig.5 The waveform of system(14)when τ is equal to different values

5 结论

时滞作为一种可变因素,非常容易影响CPS的稳定性.因此,本文结合恶意病毒在CPS中的传播特点,在SIQR模型[30]的基础上,引入了时滞因素,研究了带有时滞的SIQR模型的传播动力学.选取时滞作为分岔参数,利用特征方程导出了系统局部稳定性和发生Hopf分岔的充分条件.研究发现,时滞对CPS的稳定性具有重要的影响作用.当时滞的取值适当小时,CPS则处于渐近稳定状态.若时滞的取值超过了临界点,CPS会发生Hopf分岔,系统失去稳定性,此种情况不利于对恶意病毒的传播进行控制.最后通过一组仿真实例验证了理论的有效性和可行性.