伪卫星时钟同步算法的研究

黄 星， 赵 利， 蔡成林， 唐俏笑， 陈振林

(桂林电子科技大学 信息与通信学院，广西 桂林 541004)

目前，伪卫星自主组网定位技术都是利用卫星导航定位的原理，系统内各个伪卫星必须达到时钟同步才能进行定位，组网内各基站间的钟差会直接影响最后的定位精度[1]。理论上，1 ns的时钟同步误差相当于10～30 cm的定位误差。

为了达到高精度的时钟同步，文献[2]针对GPS星载原子钟噪声特点，利用卡尔曼滤波和最小二乘法对钟差进行预测及估计，而没有对钟差进行修正。文献[3]建立自然选择粒子群融合算法仿真模型并结合卡尔曼滤波算法实现网络内各节点的时钟同步，但是在多核环境中其算法运行时间长，难以满足实时性的要求。文献[4]针对晶振受周围环境的影响，致使标称值与实际值不吻合的问题，提出自适用同步控制算法，并通过DSP实现时钟同步，该方案只在有线的条件下完成，受通信线的限制。文献[5]利用双天线对时钟同步进行了探讨，通过在同一伪卫星上两个发射天线采用同一时钟基准消除钟差的影响，没有对时钟同步做更深入的研究。文献[6]采用了卡尔曼滤波和跟踪迭代算法对两路时钟信号进行同步，但是该方法仅仅实现的是伪卫星辅助导航卫星，而没有实现伪卫星自主组网定位。

本文提出一种混合优化算法(Hybrid Optimizing Algorithm，HOA)，利用双天线与接收机组成的三角形，消除载波相位定位中整周模糊度的影响，并通过载波相位观测方程和最小二乘法(Least Square，LS)解算出各伪卫星基站间的钟差，然后利用卡尔曼滤波算法(Kalman Filter，KF)对解算出的钟差进行处理，最后将处理后的钟差进行粒子滤波，实现伪卫星间高精度的时钟同步。

1 时钟同步数学模型描述

时钟同步有很多的数学模型，基于局域参考站网络伪距观测数据和实时钟差解算公式建立的数学模型应用最广泛[7]。本文所提出的HOA算法是在载波相位定位方程的基础上解算钟差，其中载波相位定位方程中最重要的问题就是整周模糊度的确定[8]，为了解决整周模糊度的问题，本文在发射机处设置双天线来消除整周模糊度的影响。

1.1 伪卫星组网定位系统布局

本文所设计的伪卫星组网定位系统由4个或4个以上的伪卫星基站组成，如图1所示，其中基站均装备原子钟。针对伪卫星组网定位中的远近效应，本文设计的发射机采用不同的PRN码，降低远近效应影响；为了解决载波相位测距中的整周模糊度的问题，本文发射机采用2个发射天线，且2个天线的距离保持在半个波长之内。

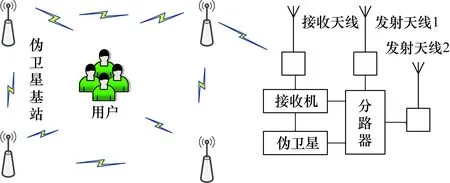
图1 伪卫星组网定位系统

1.2 时钟同步

通过参考大量的时钟网络结构模型与仿真分析[9]，采用载波相位测距的方法，通过对各基站的测距与实际距离的比较，从而计算出钟差。其原理如下：

λ(N+θ)=R+c×Δt

(1)

式中，λ为信号的波长；N+θ为收发基站间的载波相位，N为整周部分，θ为初始相位差；R为收发基站间的实际距离；c=3×108m/s为光速；Δt为基站间的钟差。

由于各个伪卫星基站的位置是已知的，所以各基站的距离可表示为

(2)

(3)

式中，(x11,y11)为主基站的第1个发射天线的位置坐标；(x12,y12)为主基站的第2个发射天线的位置坐标；(xi,yi)为i号主基站的接收机位置。

基于载波相位测距定位技术在得到多个观测值后，可建立定位方程：

(4)

由于采用了双天线设计，且距离小于半个波长，所以基站的接收机与其他基站的发射机的双天线构成三角形，根据三角形的原理知：

Ri1-Ri2<0.5δ

(5)

式中，δ为信号波长。由式(5)可知，Ri1和Ri2的距离差是由初始相位差引起，与整周模糊度没有关系，所以式(4)可改写为

(6)

式(6)可改写为

XV=R

(7)

其中，

对于式(7)的最小二乘解为

X=(VTV)-1VTR

(8)

利用观测数据解算出整周模糊度Ni1和各伪卫星基站间的钟差Δt。

1.3 卡尔曼滤波算法

卡尔曼滤波算法因迭代时间短而被广泛应用，同时出现了大量的改进算法，其中DKFCC同步算法是在分布式卡尔曼得到时钟参数最优估计的基础上，通过一致性补偿实现时钟同步[10]。本文针对最小二乘法解算出的钟差，设计出合适的卡尔曼滤波算法，将解算得出的各伪卫星基站间的钟差Δt作为卡尔曼滤波算法的输入，即y=Δt，卡尔曼滤波器的更新过程如下：

x(k)=x(k-1) 状态预测

p(k)=φ(k)p(k-1)φ(k)T+Q协方差预测

K(k)=p(k)HTR-1卡尔曼增益

x(k)=x(k)+K(k)×(y(k)-x(k)) 状态更新

p(k)=(1-K(k)×p(k)) 协方差更新

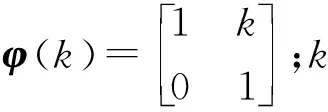
1.4 粒子滤波算法

将卡尔曼滤波后的钟差作为粒子滤波的输入，即T=x(t)，具体的粒子滤波过程如下。

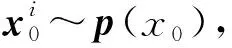
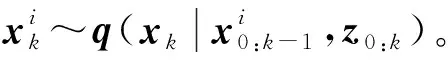
计算重要性权值如下：

⑤ 判断是否结束，若是则退出算法，否则返回②。

1.5 定位方法的选择

为了验证时钟同步对伪卫星组网定位[15]的影响，本文采用具有高精度的载波相位测距的方法，其原理如下：

λ(N+θ)=R1+c×Δt

(9)

式中，R1为用户与各伪卫星基站间的距离。

(10)

式中，(xi,yi)为伪卫星基站的任意一个发射天线的位置坐标；(x,y)为待求用户坐标位置。通过对各基站时钟同步前后的定位精度对比，验证了本文算法的有效性。

2 HOA算法分析

时钟同步是伪卫星组网定位最基本的问题，也是影响定位精度的关键问题。本文通过采集大量的观测数据，并利用Matlab 2014平台对采集的数据进行处理，实现高精度的时钟同步。HOA算法流程如下。

① 利用嵌入式DSP平台设计伪卫星接收机，如图2所示，采集发射机的测距数据；

② 提取采集数据中的初始相位差信息，即θ的值；

③ 将所得θ值代入到式(7)，利用最小二乘法解算出整周模糊度N以及钟差Δt；

④ 将所得钟差Δt作为卡尔曼滤波的状态方程，进行卡尔曼滤波处理；

⑤ 将卡尔曼滤波处理后的钟差进行粒子滤波，实现各个伪卫星间的高精度时钟同步；

⑥ 对粒子滤波处理后的钟差代入式(9)，通过多个历元数据解算出待求用户坐标信息；

⑦ 若所求待求点坐标不满足定位精度，则重新采集数据，重复①～⑥，直到满足定位精度要求。

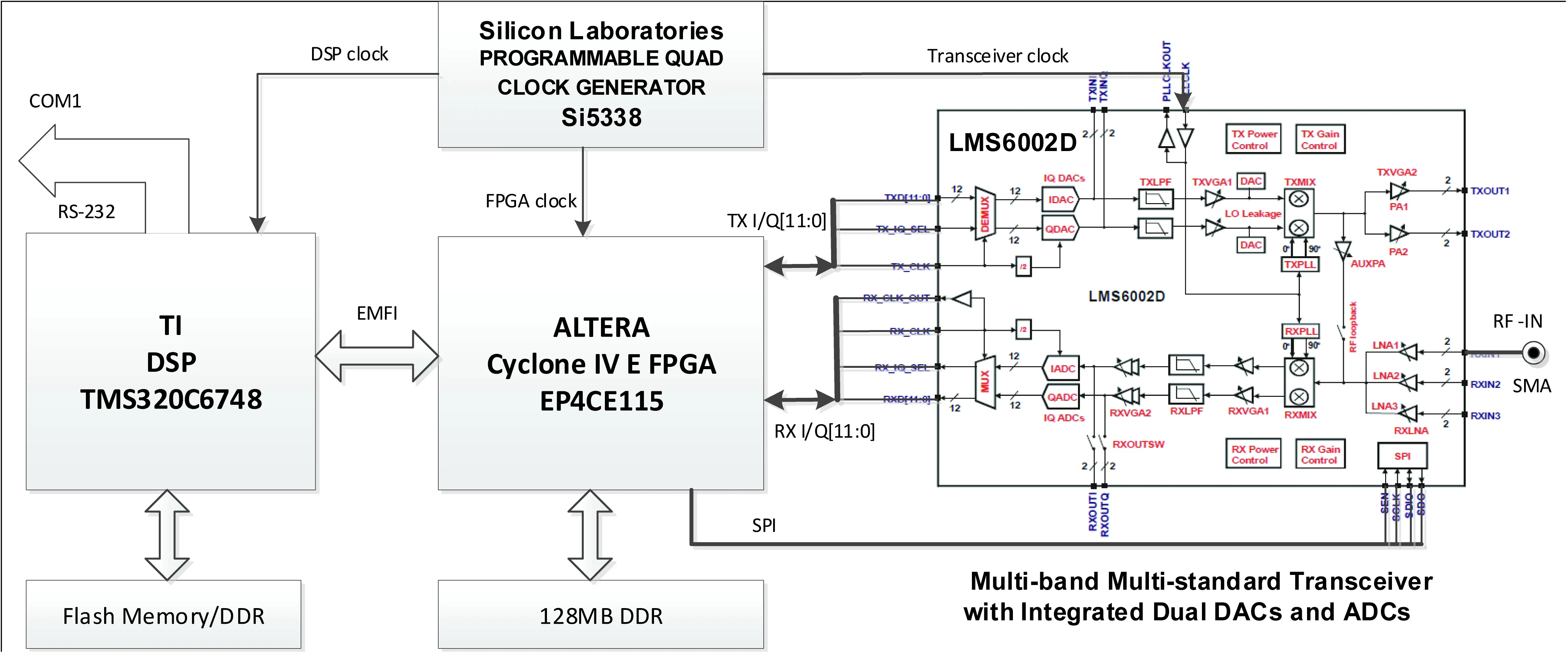
图2 伪卫星接收机原理图

HOA算法开创性地将卡尔曼滤波算法和粒子滤波算法有机地结合，通过对卡尔曼已有的算法进行参数的更改，以达到缩小钟差的目的，并将所得钟差进行粒子滤波，针对输入钟差设计出新的权重，完成高精度的时钟同步要求。

根据上述算法流程，本文采集了100个历元的发射机数据进行Matlab仿真。通过提取相位差观测值采用最小二乘法解算出伪卫星之间的钟差，如图3所示。将解算出的钟差作为输入方程，进行卡尔曼滤波、粒子滤波和HOA算法处理，滤波后各钟差如图4所示。

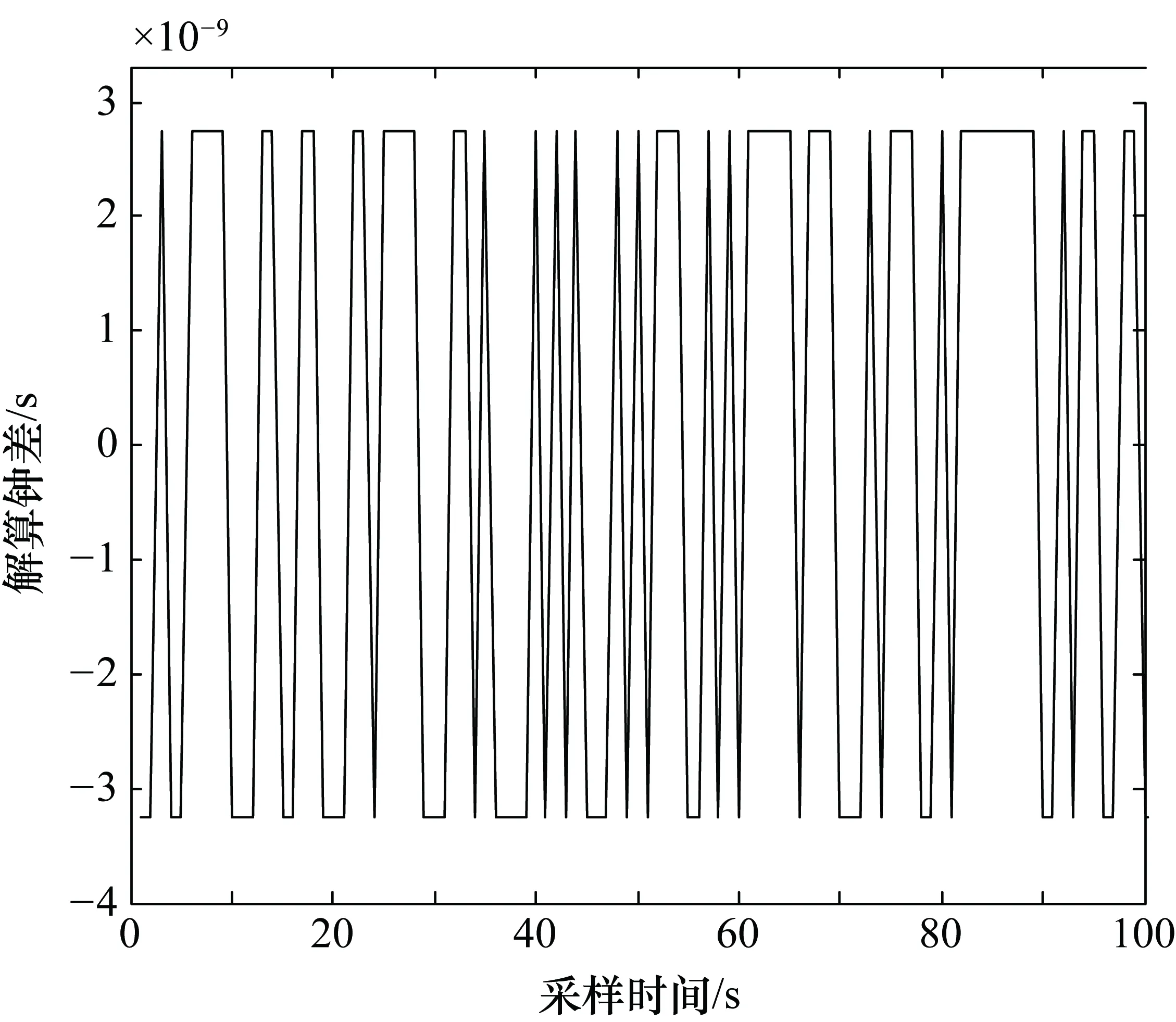
图3 伪卫星间的钟差

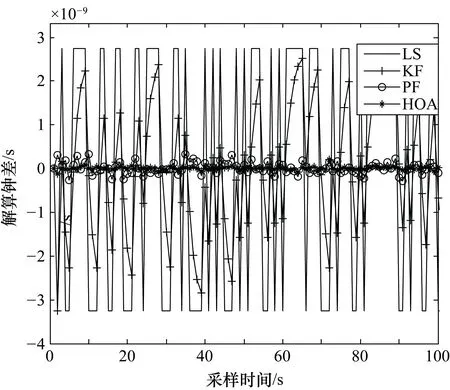
图4 滤波后的钟差

通过图4的实验结果可以发现，HOA算法和粒子滤波算法(PF)能够更好地缩短钟差，其同步精度更高。为了更好地对比出各算法的优缺点，本文利用两次卡尔曼滤波算法(Liangci Kalman Filter,LKF)和两次粒子滤波算法(Liangci Particle Filter,LPF)与HOA算法对比，其结果如图5所示。

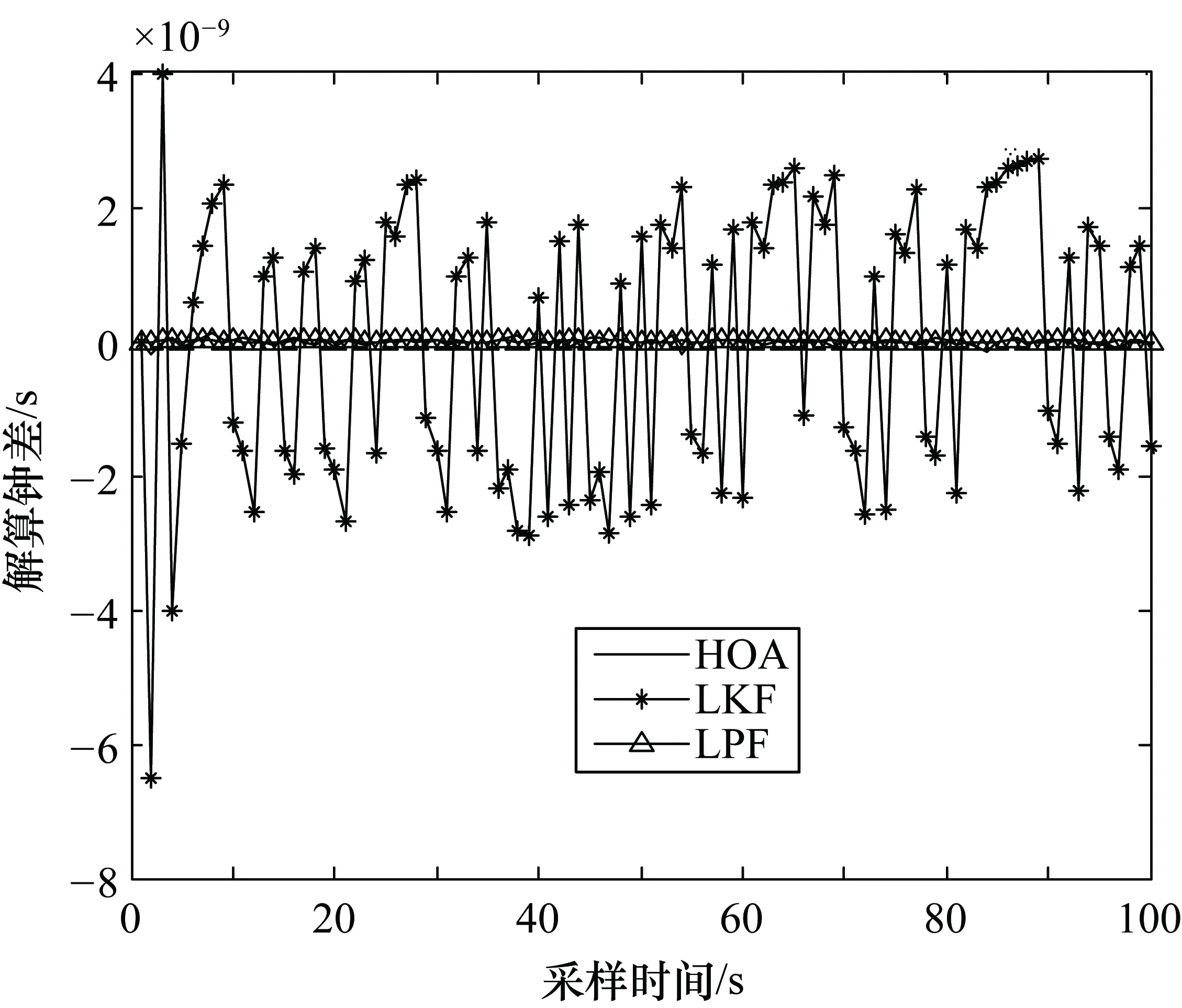
图5 两次滤波后的钟差

表1是由1000个历元数据所得的结果，其中均值由各元素取绝对值后所得，由此可知粒子滤波算法可以将钟差缩小一个数量级，但是其运算时间长，实时性差。最小二乘算法和卡尔曼滤波算法无法完成更高精度的时钟同步，两次卡尔曼滤波后的钟差精度也无法提高，但是其实时性明显高于粒子滤波算法。本文HOA算法的同步精度明显高于最小二乘算法和粒子滤波算法，其同步精度要低于两次粒子滤波算法。就实时性而言，HOA算法充分利用了卡尔曼迭代时间短的优点，能够快速地将最小二乘法解算出的钟差进行滤波处理，使得粒子滤波算法具有更好的初始化粒子，可以缩短粒子滤波算法的迭代时间，因此其实时性高于粒子滤波算法和两次粒子滤波算法。

表1 各算法同步精度与解算时间对比 单位：s

将HOA算法处理后的钟差代入到载波相位观测方程中进行用户位置解算，由于起始数据对定位结果影响较大，所以舍去了前100个数据，其定位结果均方根误差如图6、图7所示。其中图6为经过卡尔曼滤波后的钟差对定位结果的均方根误差，图7为经过HOA算法后的钟差对定位结果的均方根误差。由图6、图7可知，组网内伪卫星时钟未同步的情况下可实现分米级的定位，而钟差经过HOA算法处理后，可实现厘米级的定位。

由上述定位结果均方根误差可知，HOA算法能够有效地提高时钟同步精度，从而提高伪卫星组网的定位精度。通过对位置的解算，验证了本文方法的可行性。

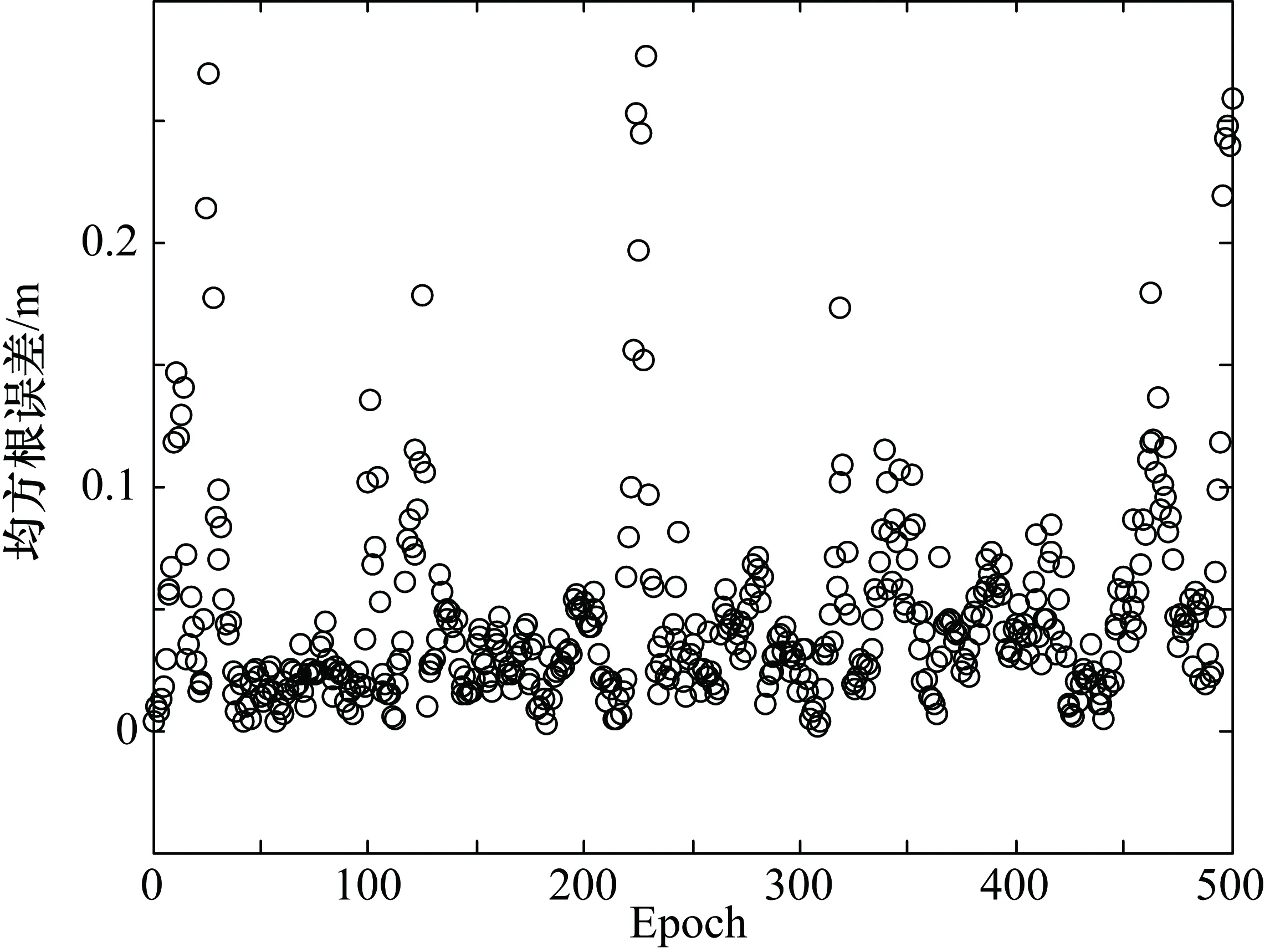
图6 同步前定位均方根误差

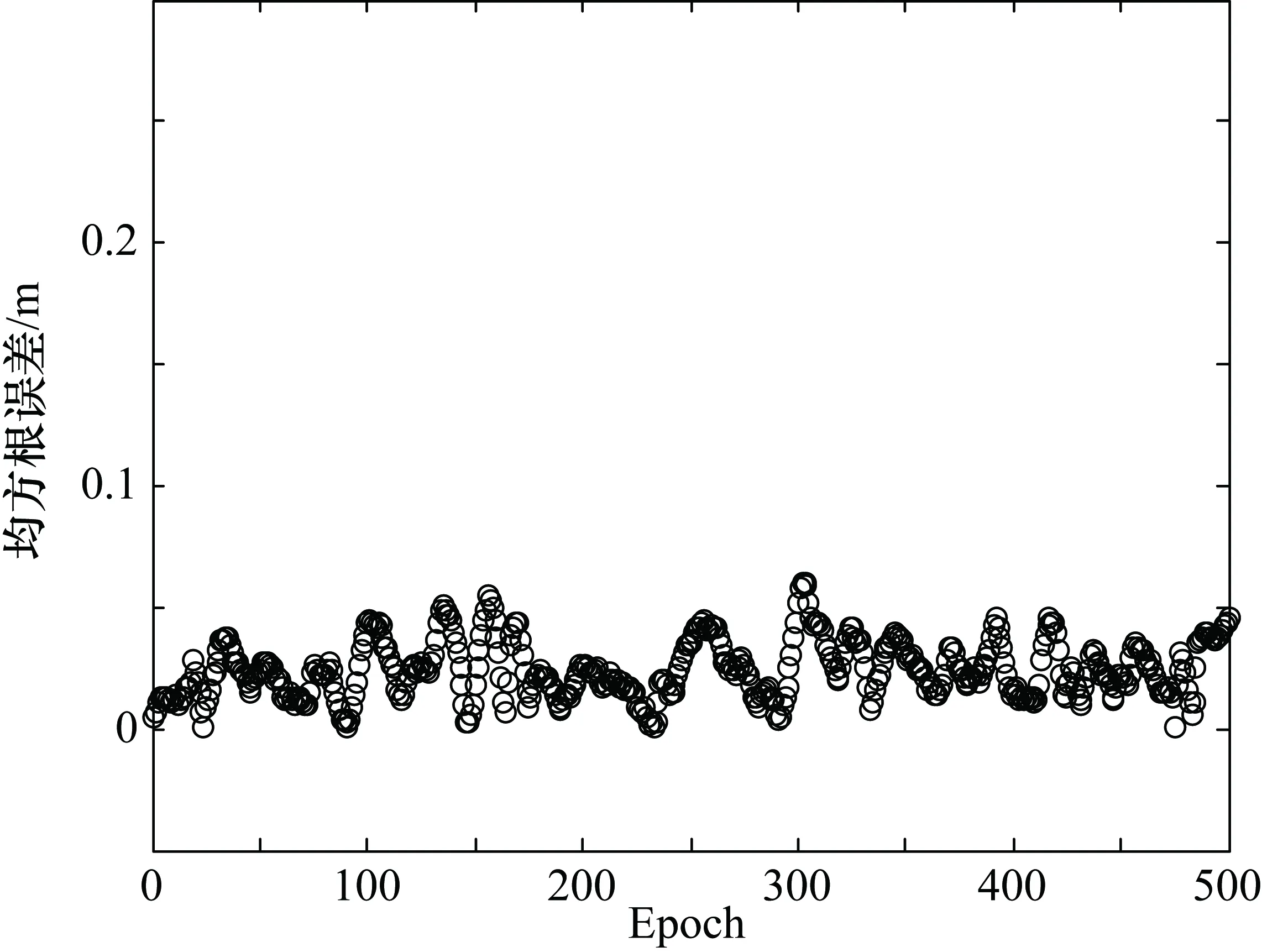
图7 同步后定位均方根误差

3 结束语

针对伪卫星组网定位中伪卫星网络时钟同步问题展开研究，提出HOA算法，将卡尔曼滤波算法迭代时间短和粒子滤波算法精度高有机结合，充分利用了卡尔曼滤波算法和粒子滤波算法的各自优势，提高了整个同步过程的精度和效率。相较于卡尔曼滤波算法，虽然实时性降低了，但是其同步精度提高了一个数量级。HOA算法与经典粒子滤波算法相比，具有精度高、迭代时间短的优势。所研究的混合优化滤波算法对提高伪卫星定位精度具有一定的参考价值。