基于S-PMemetic算法的电站锅炉再热器系统建模

许 壮, 张经纬, 康英伟, 周 昊

(上海电力大学 自动化工程学院, 上海 200090)

我国能源资源约束日益加剧,以雾霾为代表的生态问题突出,使得环境问题成为与能源发展联系最为密切的问题之一。超超临界机组锅炉再热循环系统得到更好控制的前提是在了解该热工过程静态和动态特性的基础上,建立能描述再热器系统的完整的数学模型。再热器具有复杂热工对象所普遍存在的非线性、时变性、大迟延和大惯性等特点,而且在超超临界机组上体现得更加明显,使机理建模法的应用较为困难。

在已有的文献中,采用系统辨识方法所建立的再热器系统模型包含多种模型。基于智能理论的系统辨识方法有多种,如神经网络辨识法[1-4]、模糊逻辑辨识法[5]、遗传算法辨识法[6]、群智能优化算法辨识法(包括粒子群算法辨识法、蚁群算法辨识法等)等。韩璞和黄宇等人[7-8]利用量子粒子群算法(Quantum-behaved Particle Swarm Optimization,QPSO)对热工对象进行了辨识,分别得到1 000 MW超超临界机组锅炉主汽温控制系统模型和循环流化床锅炉煤风量与床层温度之间的传递函数关系式。高文松等人[9]提出了一种改进后的粒子群优化(Particle Swarm Optimization,PSO)算法应用于热工过程模型辨识,基于选择和变异机制,并通过该算法仿真模型与基本PSO算法的对比验证了改进效果。

由于包括再热器系统在内的热工过程对象大多为复杂的多变量系统,就催生了对多变量系统辨识的研究。袁世通等人[10]提出了一种新型多入多出系统的建模方法进行辨识,确定了模型结构和各参数的初始值,最后根据实际运行数据对辨识结果进行了优化校正。

PSO算法在单变量系统辨识上取得了成功,但基本PSO算法迭代后期收敛速度较慢,容易陷入局部最优解的问题。模拟退火(Simulated Annealing,SA)算法能很快地在该局部区域内发现最优解。为了提升模型参数估计的精度和速度,本文将基本PSO和SA算法相结合形成S-PMemetic算法,并将其作为模型参数估计的算法。基于660 MW超超临界机组直流锅炉再热器系统的现场数据,设计多组辨识实验,利用S-PMemetic算法进行模型的参数估计,建立低温和高温再热器的传递函数模型,以期为再热器的控制和运行优化奠定基础。

1 多数据组并行辨识问题

2输入1输出子系统如图1所示。文献[11]通过仿真实验证明了利用一组数据并通过QPSO不能准确辨识出图1中的模型参数。然后,研究者提出利用两组数据并行辨识2输入1输出系统的方法,并通过仿真验证了该方法的正确性。

图1 2输入1输出系统框图

2输入1输出多变量辨识问题可以表述为二元一次方程求解问题,公式如下

u11G1+u12G2=y1

(1)

利用u11,u12,y1求解G1和G2,定会得到无穷多个解,即仅仅通过u11和u12是无法决定唯一组G1和G2值的,如果利用u11,u12,y1和智能优化算法去辨识G1和G2,也不会得到正确的结果。

因此,要使式(1)有唯一解,则需要另一组数据u21,u22,y2与第一组数据组成二元一次方程组。公式如下

(2)

依此类推,n输入1输出的多变量辨识问题可以表述为具有n个未知数G1,G2,G3,…,Gn的非齐次线性方程组求解问题。公式如下

(3)

式中:Gi——多变量系统的各子系统的模型;

i——数据组编号,i=1,2,3,…,n；

j——子系统编号,j=1,2,3,…,n;

uij——第i组数据对子系统j的输入;

n——多变量系统子系统的个数。

要想求解具有n个未知数的方程,则需要n个方程组成方程组的形式,每个方程代表一组输入对系统的激励。因此,可以得出推论:为了准确辨识出n输入1输出系统子系统的模型参数则需要利用n组不同的数据进行并行辨识。

再热器的输入参数为入口蒸汽流量、入口蒸汽温度、机组负荷指令,这3个变量作为式(3)中的u11,u12,u13,输出变量出口蒸汽温度为y1。再热器的模型为3输入1输出的系统,而PSO算法只能对单输入单输出的模型进行辨识,因此可以利用3组不同的数据对再热器的系统进行并行辨识,组成三元一次方程组得到唯一解G1,G2,G3,即再热器系统3个输入与输出的传递函数式。因此,可以利用多数据组并行辨识方法进行再热器的传递函数参数估计。

2 S-PMemetic算法

Memetic算法是MOSCATO P在1989年提出的建立在模拟文化进化基础上的优化算法,其实质上是一种基于群体的计算智能方法与局部搜索相结合的一类算法的总称。PSO算法能在较短时间内找出解空间内的优秀区域[12],SA算法能很快地在该局部区域内发现最优解,而Memetic算法可以说是基于种群的全局搜索算法(如PSO)和基于个体的局部启发式搜索算法(如SA)的结合体。相比一般的进化算法,Memetic算法具有更高的准确度,适用于高维、动态问题的求解,但其结构较复杂,执行速度偏慢[13]。

目前国内对Memetic算法的相关研究不多,由于Memetic算法是全局搜索策略和局部搜索策略的结合,文献[14]提出了两种算法框架:两种策略顺序执行的S-PMemetic算法和两种策略交替执行的A-PMemetic算法。因此,本文选用PSO算法和SA算法顺序执行的S-PMemetic算法,并用于再热器多系统辨识建模的研究。

2.1 PSO算法

PSO算法通过有限粒子在一定空间内按照既定公式随机移动,来寻找空间内满足某个条件的最估值。算法采用实数编码方式,需要调整的参数较少,易于实现,是一种通用的全局搜索算法。

在D维搜索空间中,第i个粒子的无量反弹速度分别为X=(xi,1xi,2xi,3…xi,D)和V=(vi,1vi,2vi,3…vi,D),在每次迭代中,粒子通过跟踪两个最优解来更新自己:一是每个粒子自身所经历过的最优位置pbest;二是整个种群经历过的最优位置gbest。在找到这两个最优值时,更新粒子的速度和位置找到新种群。若满足预设的运算精度或迭代次数，结束寻优，输出结果，否则继续搜索。

2.2 SA算法

SA算法是基于蒙特卡罗算法结构来求解的一种启发式随机搜索算法,取自物理学中退火过程的概念,即对固体物质进行退火处理时,通常先将其加热到某一温度,使内部粒子进行较大振幅的自由运动,然后降温操作,粒子逐渐形成较低能态的晶体。

该算法的基本思想是开始时给出一个试探解,然后从其邻域中随机产生另一个解,这个新解要受到Metropolis提出的规则的限制,这样目标函数在设定的范围内变化。这个变化过程由一个参数t决定,t的作用类似于物理过程中的温度T。对于控制参数t的每一个取值,SA算法持续进行“产生→判断→接受(或舍去)”多次迭代计算,控制参数t逐渐减小趋于零的计算过程对应着固体在某一恒定温度下趋于热平衡的过程。最后,所考虑的系统状态就对应于优化问题的全局最优解。这个过程可以称为冷却过程。由于固体退火过程要求缓慢降温,所以控制参数t要进行缓慢的衰减过程。这样才能使得固体在每一温度下都达到热平衡状态,并确保SA算法最终优化问题的整体最优解[15]。

实际上SA算法包括两重循环,即参数的随机扰动和温度降低。该算法初始温度要求设计在高温位置,使得目标函数值增大的情况可能被捕捉到,因而可以舍弃局部极小值。通过缓慢降低温度,算法最终可以收敛在全局范围上的最小点。

2.3 S-PMemetic算法流程

图2为S-PMemetic算法流程。在PSO算法执行完后会对全局最优解进行随机扰动并产生新解,然后根据SA算法进行局部寻优,得到最终的优化结果。

图2 S-PMemetic算法流程

3 再热器系统建模辨识

对再热器系统过程机理的认识,可确定再热器系统建模框架,具体如图3所示。图3中,ΔD1和ΔD2为低温再热器入口蒸汽流量,ΔH1为低温再热器入口蒸汽温度,Δθ为低温再热器出口的烟气挡板开度,ΔP为机组的负荷指令,ΔH2为低温再热器出口蒸汽温度(高温再热器入口蒸汽温度),ΔH3为高温再热器出口蒸汽温度,Gi(s)(i=1,2,3,…,7)分别表示各通道的传递函数关系式。本文通过改进PSO算法和多组数据并行辨识的方法辨识出每个传递函数的结果。

3.1 低温再热器各通道并行辨识

低温再热器的输入分别为入口蒸汽流量、入口蒸汽温度、机组负荷指令和烟气挡板开度等4个物理量,其中前3个物理量存在明显的耦合关系。因此,利用PSO算法对烟气挡板开度传递函数通道进行单变量辨识,而利用S-PMemetic算法对其他3个输入变量传递函数通道进行多数据组并行辨识,3组辨识数据均经过零均值化和小波滤波处理。机组负荷指令通道的传递函数辨识模型为

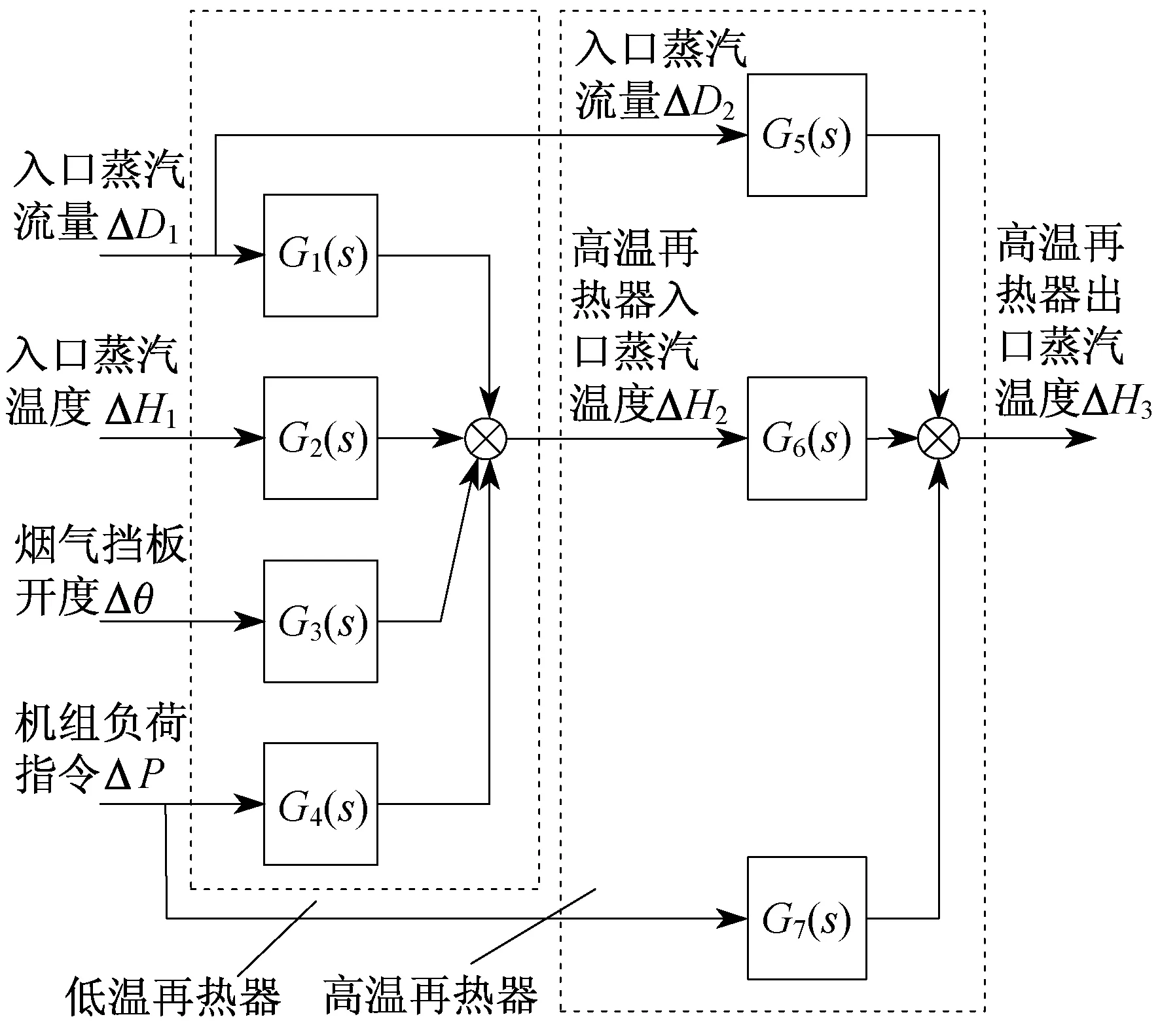
图3 再热器系统建模结构

(4)

其他3个通道的传递函数辨识模型为

(5)

利用PSO算法对烟气挡板开度传递函数通道进行辨识,辨识数据为在75%额定工况下烟气挡板开度阶跃减小30%的数据段,算法的参数设置不变,辨识结果为

(6)

辨识误差J=0.3182。

在利用S-PMemetic算法进行多数据组并行辨识前,对传递函数表达式中的放大系数进行放缩,以各参数估算值为基点将搜索范围上限扩大为两倍,而辨识数据的负荷在50%～75%之间变化,所以将搜索范围下限缩小为4倍,即K1∈[-0.50,-0.05],K2∈[0.25,2.00],K4∈[0.08,0.64]。PSO算法的迭代次数G=100,SA算法的初始温度T0=1 000 ℃,Metropolis链长L=200,辨识结果为

(7)

(8)

(9)

辨识误差J=3.292 8。

低温再热器模型多数据组辨识曲线和辨识误差如图4和图5所示。由图4和图5可以看出,辨识误差基本在±3 ℃以内,搜索范围缩小后,辨识效率明显加快,基于S-PMemetic算法的多变量并行辨识效果较为理想。

图4 低温再热器模型多数据组辨识曲线

图5 低温再热器模型多数据组辨识误差

3.2 高温再热器各通道并行辨识

利用S-PMemetic算法,对高温再热器入口蒸汽流量、入口蒸汽温度和机组负荷指令3个输入变量对应的传递函数通道进行多组数据并行辨识,系统模型多数据组辨识曲线和辨识误差分别如图6和图7所示。

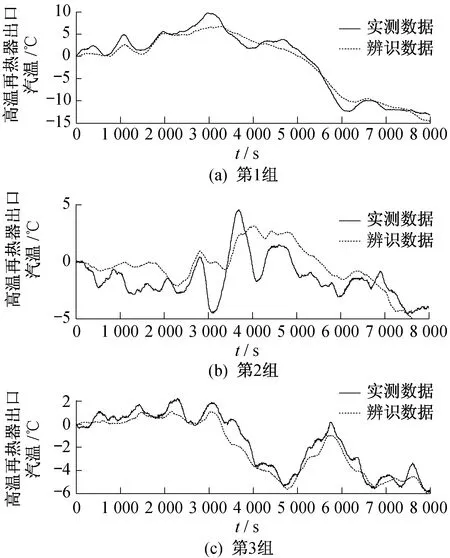
图6 高温再热器模型多数据组辨识曲线

图7 高温再热器模型多数据组辨识误差

搜索范围为K5∈[-0.60,-0.075],K6∈[0.25,2.00],K7∈[0.09,0.54]。辨识结果为

(10)

(11)

(12)

辨识误差J=3.767 6。

4 结 语

本文首先对多数据组并行辨识问题进行理论分析,得到了辨识出n输入1输出系统子系统的模型参数需要利用n组不同的数据进行并行辨识的推论。

采用S-PMemetic算法辨识得到的再热器系统模型很好地解决了多变量融合建模困难的问题。S-PMemetic算法平衡了PSO算法的全局搜索能力和SA算法的局部寻优能力,更适用于辨识复杂的热工控制对象,进一步提高多变量辨识效率和精确度。

采用该辨识方法建立的再热器系统模型为再热器系统的控制和运行优化打下了坚实的基础,为复杂多变量融合系统的辨识提供了有益的思路。