基于模糊PI控制的双同步解耦坐标系三相不平衡锁相环设计

葛祥一, 邓 亮, 王龙飞

(1.上海电力大学, 上海 200090; 2.深圳乐生机器人智能科技有限公司, 广东 深圳 518000; 3.桂林电子科技大学, 广西 桂林 541004; 4.国网河南省电力公司, 河南 安阳 455000)

为克服传统大电网供电安全要求高且可靠性较差的不足,自20世纪80年代以来,分布式发电技术受到广泛的重视和应用。当分布式发电系统接入电网运行后,并网变换器起着重要作用[1-3]。并网变换器控制系统需实时监测电网电压相位情况,在电网电压发生畸变和不平衡时,锁相环系统必须能精确实时检测到电网电压相位信息。因此,锁相环的精度在一定程度决定了系统性能的精度[4-7]。

电网电压相位角可通过将电网电压作为同步信号获得,然而,该方法会因电网电压波形失真而使系统输出电压和电流发生畸变,进而在一定程度上影响系统稳定性。在理想电网电压的情况下,单同步坐标系的锁相环可快速精确检测电网电压幅值和相位信息,但当电网电压受到扰动而发生不平衡或畸变时,不能精确输出系统相位信息[8-10]。针对单同步锁相环不易消除二次谐波的缺点,文献[11-12]提出了基于双同步解耦坐标系的锁相环设计方法,可通过交叉解耦消除二次谐波获得三相不平衡电压的直流量。文献[13]提出了基于二阶广义积分器的改进型双同步解耦坐标系锁相环,可利用广义积分器良好的滤波能力实现谐波的滤除。然而,以上方法均使用固定的PI参数,无法在线修改,不具有适用性。

模糊控制因其鲁棒性强、响应快速且无需精确建模等优势而被广泛应用于电力系统、电力电子和电机控制等领域[14-16]。相较传统锁相环,结合模糊控制器的锁相环采用模糊算法优化模糊隶属度函数,可使锁相环具有更好的适用性、动态特性与稳态性能[17-18]。基于模糊控制的变带宽锁相环跟踪目标的稳定性和测量精度均优于传统锁相环[19-20]。针对上述锁相方法及单独使用模糊控制动态品质差和控制精度低的不足,本文提出了一种基于模糊PI控制的双同步解耦坐标系三相不平衡锁相环设计方法,将电网电压正序基波分量通过双同步解耦坐标系分离作为模糊PI系统的闭环输入,以实现对电网电压正序基波分量相位的精确检测。

1 锁相环基本原理

锁相环实质为一个闭环的相位调节系统,基本组成如图1所示。采用压控振荡器输出与系统输入之间的误差信号控制压控振荡器输出频率。当这两个信号之间的频率误差为零、相位误差不随时间变化且误差控制电压为定值时,即认为系统进入锁定状态。

图1 锁相环电路基本组成

图1中:ur(t),θr(t)为系统输入电压参考信号及其相位;e(t)为误差信号;uy(t)为控制信号;uo(t),θo(t)为压控振荡器输出电压信号及其相位。

2 双同步坐标系解耦锁相环基本原理与设计

2.1 双同步坐标系解耦锁相环基本原理

假定一个电压矢量包括正序分量和负序分量,分别以ωn和ωm的角速度进行旋转,n表示正序,m表示负序,ω表示基波电网频率。该电压矢量可表示为

(1)

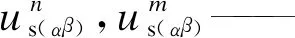
φn,φm——正序矢量和负序矢量的初始相位。

假设旋转坐标系分别用dnqn和dmqm表示,θn和θm为两个旋转坐标系的角度,θ′表示锁相环输出角度。若锁相精确,即θ′=ωt,则电压矢量us(αβ)在dnqn和dmqm系中可表示为

(2)

(3)

在dnqn与dmqm旋转坐标系中,振荡量的幅值分别由dmqm和dnqn坐标系中的平均值确定。为了对dnqn和dmqm坐标系中的振荡量进行削弱,需要对双同步坐标系解耦锁相环结构进行设计。

2.2 双同步坐标系解耦锁相环结构模型设计

通过以上分析可知,在正负序dq坐标中各输出电压存在一定联系,即可进行解耦计算。此处设n=1,m=-1,电压矢量分解到d+1q+1和d-1q-1两个同步旋转坐标系上,两个坐标系中的直流分量与电网电压正负序分量的幅值有很大关系。正序和负序电压解耦变换公式分别为

(4)

(5)

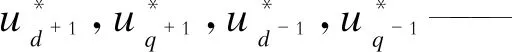
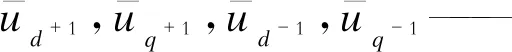
θ′——解耦网络的电压输出相位。

图2 基于双同步解耦坐标系的三相锁相环系统结构

图2中LPF(low-pass filter)模块为低通滤波器(截止频率为ωf),可过滤掉电压中的高次谐波。其传递函数为

(6)

2.3 双同步坐标系解耦锁相环控制参数设计

图2中,基于双同步解耦坐标系的锁相环控制系统含有非线性部分,故只能对其进行近似性能分析。当相角误差较小时,该系统等效传递函数可与单同步坐标系锁相环相同,系统开环和闭环传递函数分别为

(7)

(8)

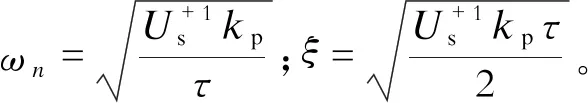
为了分析方便,假设初始相位角φ+1=0,φ-1=0,正序分量幅值的阶跃响应计算公式为

(9)

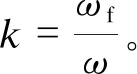
3 模糊PI双同步锁相环设计

3.1 模糊控制器输入输出量设计

模糊控制器采用双输入双输出结构,输入变量为e及其变化率Δe,输出变量为Δkp与Δki。根据双同步锁相环仿真结果设置输入输出参数,其中,e∈[-1,1],Δe∈[-0.1,0.1],Δkp∈[-2,2],Δki∈[-1,1]。在输入输出语言变量的量化域内取{NB NM NS ZO PS PM PB}7个子集,输入输出量化论域如下:

e→{-1,-0.8,-0.6,-0.4,-0.2,0,0.2,0.4,0.6,0.8,1};

Δe→{-0.1,-0.08,-0.06,-0.04,-0.02,0,0.02,0.04,0.06,0.08,0.1};

Δkp→{-2,-1.6,-1.2,-0.8,-0.4,0,0.4,0.8,1.2,1.6,1};

Δki→{-1,-0.8,-0.6,-0.4,-0.2,0,0.2,0.4,0.6,0.8,1}

3.2 隶属度函数和模糊控制表

模糊逻辑输入e和Δe以及输出Δkp和Δki的隶属度函数取为灵敏性较强的三角函数。面积重心法具有更平滑精准的输出推理控制,即使输入信号发生微小变化,输出也会发生变化。为获得准确的控制量,反模糊化采用面积重心法,取隶属度函数曲线与横坐标围成面积的重心为模糊推理的最终输出值,即

(10)

式中:vo——输出变量;

V——输出论域,v∈V;

uv——隶属度。

在MATLAB软件中完成反模糊化计算。 Δkp与Δki的模糊规则表如表1和表2所示。

表1 Δkp的模糊规则

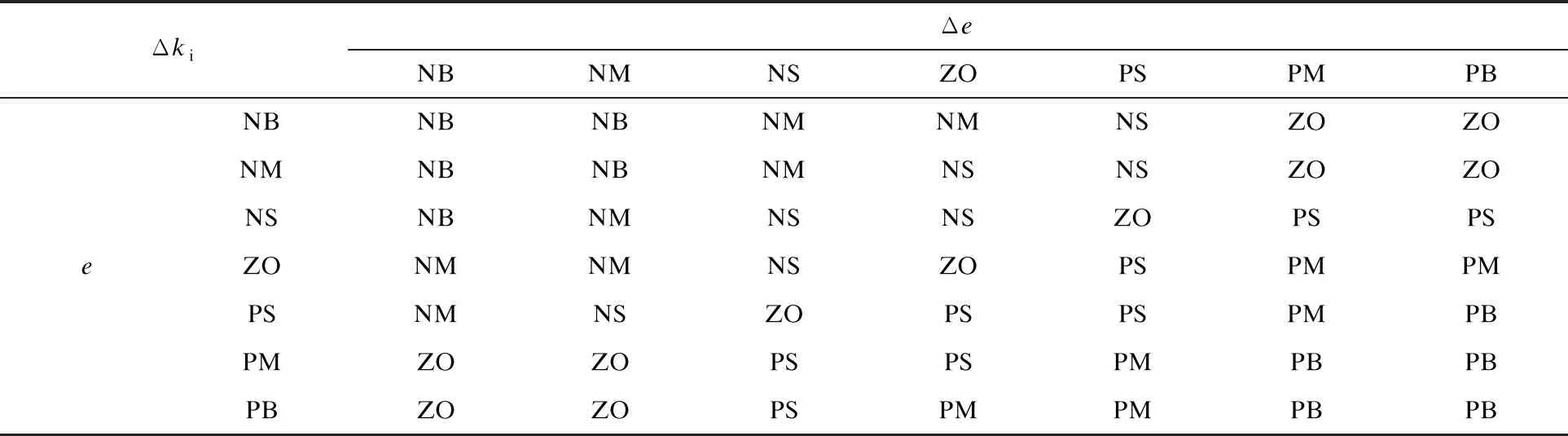
表2 Δki的模糊规则

4 仿真分析

4.1 仿真模型

为了对基于模糊PI控制的双同步解耦坐标系三相不平衡锁相环性能进行验证,采用软件MATLAB Simulink组件进行仿真。

结合其工作原理和系统结构框图搭建的仿真模型如图3所示。

图3 模糊PI双同步解耦坐标系三相锁相环仿真模型

4.2 仿真结果

双同步解耦坐标系下锁相环参数设置为:PI控制器参数kp=200,ki=112,阻尼系数ξ=0.707,自然振荡频率ωn=35 rad/s,输入电压幅值U=1.0 p.u.(p.u.为电压标幺值),频率f=50 Hz。将基于模糊PI控制的双同步解耦坐标系锁相环与双同步和单同步坐标系锁相环仿真结果进行比较。

4.2.1 电网电压平衡时仿真结果

电网电压平衡时仿真结果如图4所示。由图4可知,基于模糊PI控制的双同步解耦坐标系下三相锁相可在电网电压平衡时更快恢复三相电压且相位输出波动较小,能更准确快速地锁定正序基波相位信息。

4.2.2 电网电压不平衡时仿真结果

在理想输入电压上叠加0.3 p.u.且初始相位为30°的基频负序谐波,仿真结果如图5所示。模糊PI控制的双同步解耦坐标系三相锁相环在电网电压出现基频负序谐波时,因其可在线调整PI参数,故能更快速恢复三相电压消除负序谐波对系统的影响,更准确快速锁定正序基波的相位信息,提高系统抗不平衡电压干扰的能力。

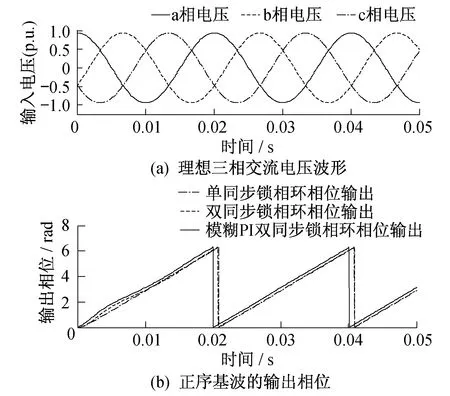
图4 电网电压平衡时的仿真波形

图5 电网电压不平衡时的仿真波形

4.2.3 低次谐波输入时仿真结果

在0.02 s时理想输入电压上叠加0.2 p.u.的5次正序谐波。低次谐波输入时的仿真结果如图6所示。当电压含一定谐波时,由于锁相结构中含有滤波器,能对谐波起到很好的抑制作用。

由图5和图6可知,相比单同步和双同步解耦坐标系下的锁相环,基于模糊PI控制的双同步解耦坐标系锁相环在电网电压含有基频负序谐波、多频正序谐波时能更准确、快速地锁定相位信息并检测到相位误差畸变小。

4.2.4 相位突变时仿真结果

在0.02 s时理想输入电压相位增加20°,相位突变时的仿真结果如图7所示。

图6 低次谐波输入时的仿真波形

由图7可知,模糊PI控制下的单同步、双同步锁相环在电压相位突变时均能保持正常电压波形,但模糊PI控制的双同步锁相环能更快消除电压相位突变给系统造成的冲击,锁定相位速度更快,具有更好的动态特性。

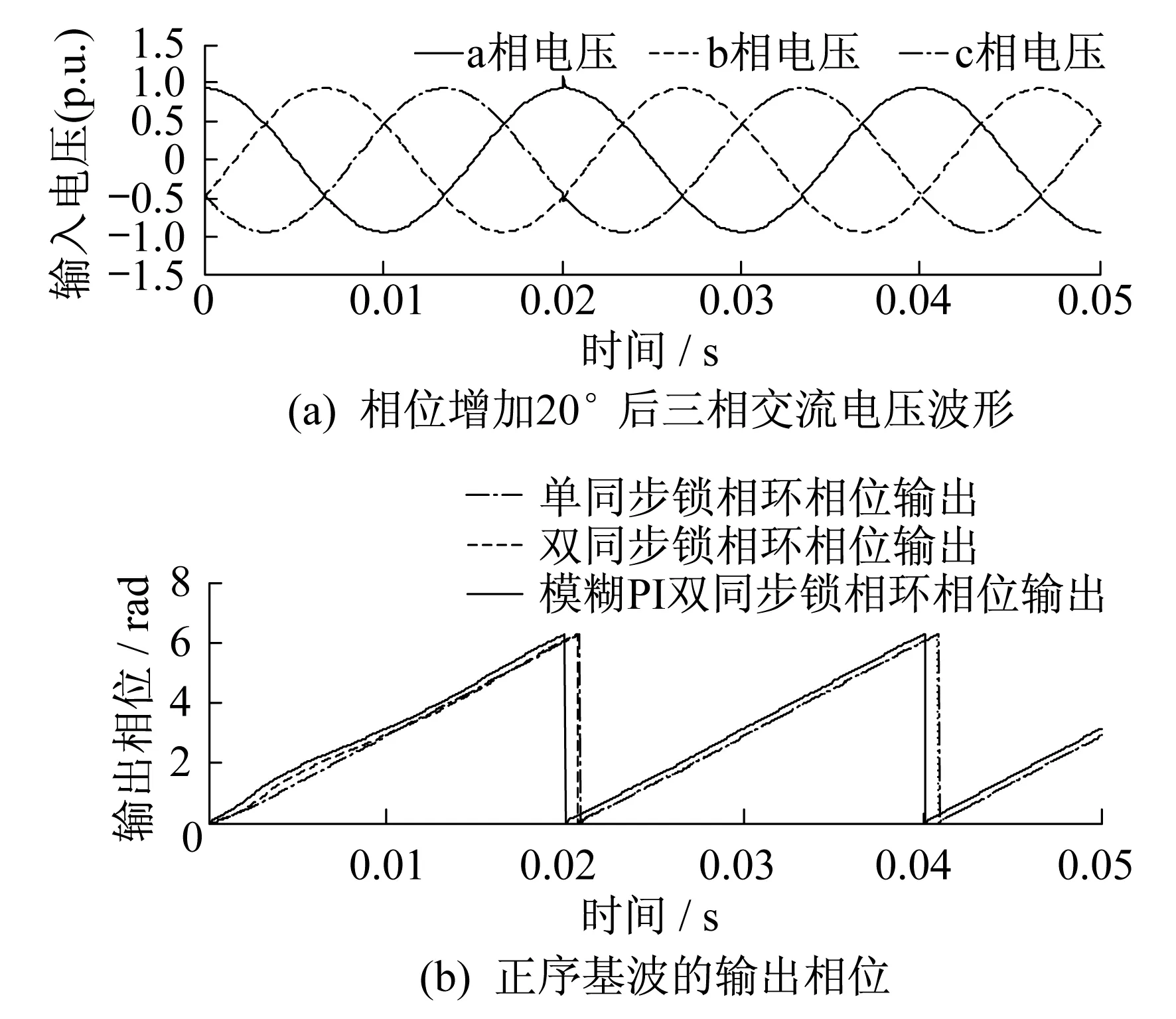
图7 相位突变时的仿真波形

4.2.5 频率突变时仿真结果

在0.02 s时理想输入电压频率从50 Hz变为54 Hz,频率突变时的仿真结果如图8所示。由图8可知,单同步和双同步解耦坐标系下的锁相环在电网电压频率突变时均可锁定正序基波相位信息并平稳地跟踪频率和相位变化,但模糊PI控制的双同步解耦坐标系锁相环锁定相位速度更快,对谐波有更强的抑制作用,表现出良好的频率适应性。

图8 频率突变时的仿真波形

5 结 语

针对双同步锁相环系统在电网发生不平衡或畸变时不能对正序基波分量的幅值和相位精确实时检测的问题,本文在双同步锁相环的基础上,提出了基于模糊PI控制的双同步解耦坐标系三相不平衡锁相环,通过解耦网络实现电网电压正序基波分量分离,并对分离出的正序基波分量的幅值和相位等信息进行精确快速检测。模糊PI控制的双同步解耦坐标系锁相环在运行中通过不断检测误差及其变化率,依据模糊规则对PI参数进行在线修正,很好地避免了传统锁相环以一组固定不变的PI参数在控制过程中运行调节的缺点,且在电网不平衡时能更快速、精确地对正序基波分量的幅值和相位进行检测,保证了分布式系统并网时对锁相精度的要求。本文仿真结果验证了所提方法的有效性。