基于SVD Entropy和SVM联合算法的列控系统态势感知技术研究

李其昌，步 兵，赵骏逸，李 刚

(1. 北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044； 2. 中国铁道科学研究院集团有限公司 通信信号研究所，北京 100081)

城市轨道交通作为典型的工业控制系统以及重要的城市基础设施，为缓解和解决城市化进程带来的交通压力和人民日益增长的交通需求，应运发展了基于通信的列车运行控制系统(Communication Based Train Control，CBTC)。CBTC系统广泛融合了计算机、通信和控制等领域的先进技术，是一个复杂的分布式、实时控制系统[1]。随着列控系统信息化与自动化的深度融合，实现了自管理信息层延伸至现场设备的一致性识别、通信和控制。

然而，在轨道交通信息化、智能化融合的同时，来自列控系统内部和外部的威胁也逐渐增大，其面临的信息安全风险日益加剧[2]。一方面，列控系统采用标准通信协议与通用计算设备，使得列控系统更易遭到黑客的攻击，如恶意木马植入、洪水攻击等；另一方面，列控系统与其他系统的数据共享、设备互联、业务协作，使得系统难以做到真正的“完全封闭”，进一步加剧了列控系统的信息安全风险。

同时，CBTC列控系统与传统IT系统以及其他工业控制系统相比，在信息安全方面存在一定区别：一是列控系统采用设备、网络冗余配置，例如ATS、ZC、VOBC等设备运行在冗余网络上，CI、ZC、ATS等关键设备采用三取二、二乘二取二或主备机等安全计算模式；二是列控系统按照时刻表运行，流量数据具有周期性、指向性等特点；三是列控系统遵循“故障导向安全”原则，即在系统发生故障的情况下，能够维持安全状态或者向安全状态转移。综上，传统的工控系统安全理论无法直接适用于列控系统，因此提出列控系统信息安全态势感知技术，以识别信息安全风险，避免列控系统安全事故发生。

列控系统信息安全态势感知(以下简称列控系统态势感知)，是指可能引起列控系统信息安全态势发生变化的态势要素获取、理解、评价以及预测的过程[3-5]。列控系统态势感知不同于现有的入侵行为检测。入侵行为检测可以检测出系统存在的受攻击行为，保障列控系统的信息安全，是一种被动防御的安全行为。列控系统态势感知则通过主动收集融合理解数据，评价当前安全态势，为列控系统的正常安全运行提供决策依据。这其中既包括对入侵攻击行为的检测，也包括为提高列控系统安全性能进行的评估与预测。

列控系统态势感知模型见图1，由态势觉察、态势理解、态势预测3个层次组成[6]。列控系统态势感知通过布设网络探针，采集物理层和网络层数据，生成多源异构数据集；再经过数据清洗与归一化，数据特征提取，数据分类技术，结合态势评价指标，完成当前列控系统安全态势理解与评价，并结合其他先进技术，实现安全态势预测。本文主要研究列控系统多源异构数据的特征提取与分类技术，并通过对列控系统数据特征提取与分类，摒弃无用信息，整理归纳数据，大幅提高列控系统态势感知的实时性，避免陷入复杂计算而无法理解实时当前态势的弊端。

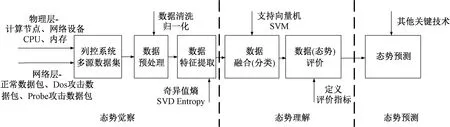
图1 列控系统态势感知模型

1 CBTC列控系统

CBTC列控系统结构示意见图2，主要由车载设备、地面设备及其数据通信系统(Data Communication System，DCS)组成。在CBTC列控系统中，区域控制器(Zone Controller，ZC)，结合计算机联锁(Computer Interlocking，CI)的进路状态、数据存储单元(Database Storage Unit，DSU)的线路数据、列车自动监控(Automatic Train Supervision，ATS)设备的临时限速信息，以及列车自动防护(Automatic Train Protection，ATP)设备(车载)汇报的列车位置和速度等信息，为其控制范围内的列车计算生成移动授权(Movement Authority，MA)，并通过无线接入点(Access Point，AP)组成的车地无线网发送给列车。正常状态下，列车车载控制器(Vehicle On-Broad Controller，VOBC)周期性接受ZC生成的MA，ATP根据MA终点基于列车动力学方程得到即刻速度防护曲线。列车自动驾驶(Automatic Train Operation，ATO)设备根据ATS制定的运营时刻表，结合旅客舒适度、列车能耗等因素，自动计算出即刻最优速度曲线，列车以此速度在速度防护曲线限定下运行。

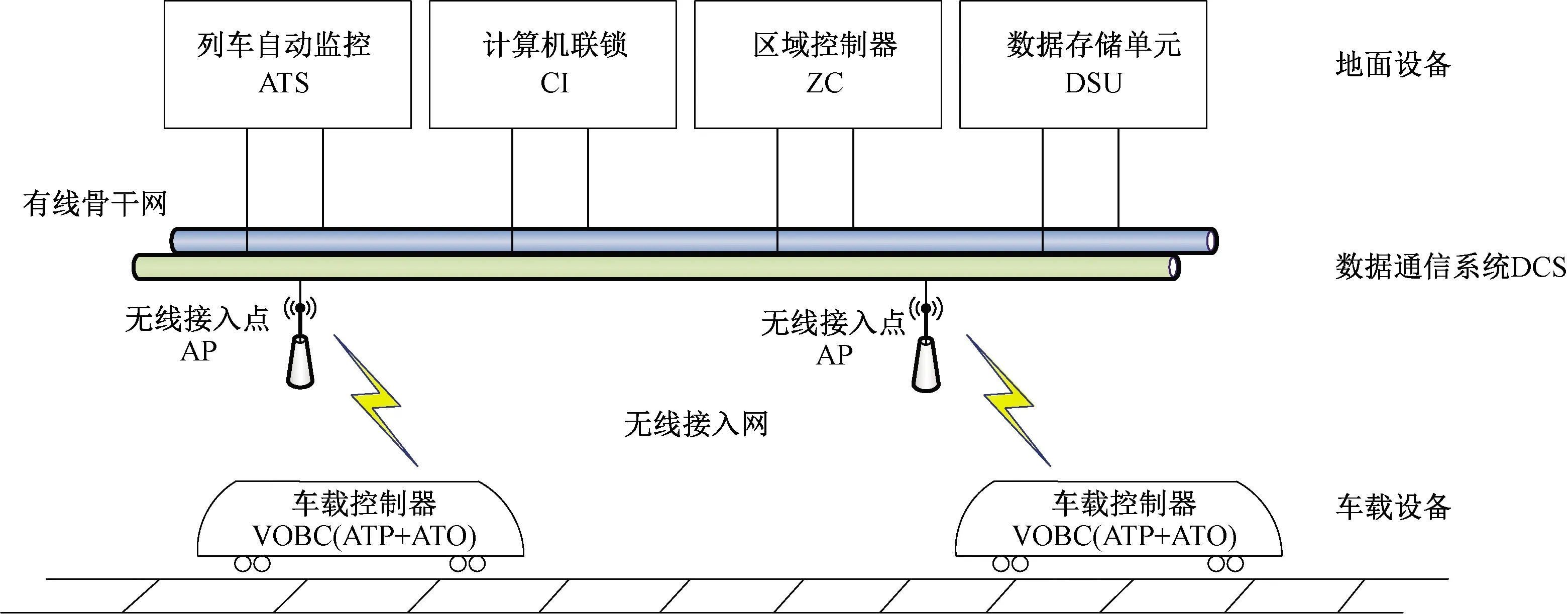
图2 CBTC列控系统结构示意图

2 列控系统态势感知关键技术

2.1 基于SVD Entropy的数据特征降维

对于任意实矩阵A∈Rm×n(一般认为m为样本数，n为特征数)，必然存在酉矩阵U∈Rm×m和V∈Rn×n，使得下式成立

A=UΣVT

(1)

式中：矩阵Σ∈Rm×n的主对角线元素λi为非负并按降序排列，且除了主对角元素以外全为0。这些对角线元素λi便是矩阵A的奇异值(Singular Value)，且有λ1≥λ2≥…≥λr>0，r=rank(A)，即矩阵A的秩为非零奇异值的个数。

根据矩阵范数性质和矩阵酉不变性质(即‖UAVT‖F=‖A‖F)可知，任一矩阵的Frobenious范数与该矩阵所有的非零奇异值平方和的正平方根相等，即

(2)

式中：aij(i=1,2,…,m；j=1,2,…,n)为矩阵A中的元素。那么，给定一个秩为r的矩阵A，可以用秩为k的矩阵Ak，k≤r，逼近表达矩阵A，则该问题用数学表达式解释为

(3)

s.t. rank(Ak)=k

(4)

如何通过确定k值进而得到近似矩阵Ak？对矩阵A做奇异值分解，得到奇异值谱λj(j=1,2,…,r)[8]。根据香农信息熵的定义，可计算矩阵奇异值分解后的奇异值熵(Singular Value Decomposition Entropy)为

(5)

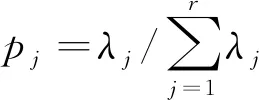
(6)

利用奇异值熵的限定条件，得到前k个有用奇异值后，将A的奇异值分解矩阵Σ中r-k个数值比重小的奇异值置零，进而得到特征降维后的多源异构数据集Ak。

2.2 基于SVM的数据分类

支持向量机(Support Vector Machine，SVM)作为一种先进机器学习算法，广泛应用于模式识别、数据分类、回归预测等方面[9-10]。其基本原理是通过划分超平面，在满足可容忍分类精度的前提下，最大化不同类别数据至超平面的间隔，并将此间隔最大化问题转变为求解二次凸规划的最优化问题，从而完成数据的分类。

假设非线性可分数据集Ak∈Rm×n；xi∈R；i=1,2,…,m；yi∈[-1, 1]。其中xi为第i个实例，yi为类标记，m为观测样本数，n为特征数。给定超平面wTΦ(x)+b=0，可将实例分为不同类别，则相应决策函数为[11]

y(x)=sign(wTΦ(x)+b)

(7)

式中：w为超平面法向量；b为超平面到空间某点距离；Φ(x)为某个确定的特征空间转换函数，其作用是将x映射到高维度，如为一维，则Φ(x)=x。将y(xi)>0分为正类，y(xi)<0分为负类，且有yi(wTΦ(xi)+b)≥1。

要寻找的唯一超平面即是以充分大置信度使样本点集到此超平面间隔最大，即尽可能使更多的样本点远离超平面，以完成分类，即

(8)

s.t.yi(wTΦ(xi)+b)≥1

其中，满足yi(wTΦ(xi)+b)=1的样本点(xi,yi)称为支持向量。当某些样本不满足其中yi(wTΦ(xi)+b)≥1的约束时，引入松弛变量ξi≥0，使最大化间隔的同时，不满足约束的样本尽可能少，则式(8)可改写为

(9)

s.t.yi(wTΦ(xi)+b)≥1-ξi

式(9)为二次规划问题，通过拉格朗日乘子法可得拉格朗日分解式为

(10)

式中：α≥0为拉格朗日乘子向量；μi≥0为常数；C>0为惩罚参数。分别对L(w,b,α,ξ,μ)求w,b,ξ的极小，求α的极大，并整理可得：

(11)

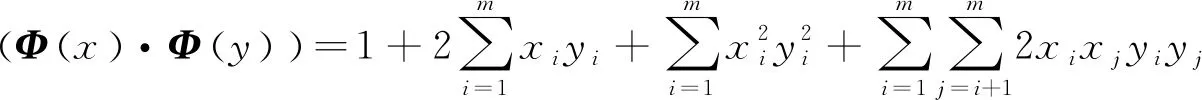
(12)

(13)

式中：(xj,yj)为任一支持向量。因此，非线性可分数据集的划分超平面与决策函数分别为

(14)

(15)

列控系统态势感知多源异构数据集为非线性可分数据集，如果其原始特征空间属性数有限，那么一定存在高维特征空间是样本可分。高维特征空间在求解划分超平面过程中，由于特征空间维数可能很高，直接计算样本xi与xj的内积(Φ(xi)·Φ(xj))比较困难，因此，通常采用核函数K(xi,xj)拟合，而不用显式地定义特征空间和映射函数Φ(x)。那么划分超平面与决策函数可表示为

(16)

(17)

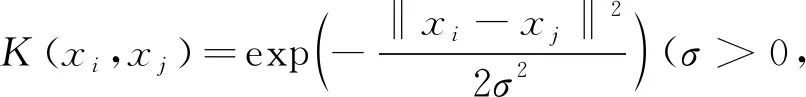
对列控系统特征降维后的多源异构数据集Ak分类需要运用多分类技术，本文采用一对一多分类方法(One-Versus-One SVM)，在任意两类样本之间设计一个分类器，当对某一未知类别样本xi分类时，最终得票最多的类别即判为该未知样本的类别。上述多分类问题的数学描述为：求解满足约束条件下使分类间隔最大的划分超平面，进而完成类别划分与投票。

(18)

s.t.

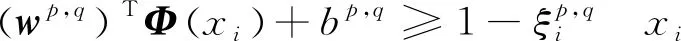
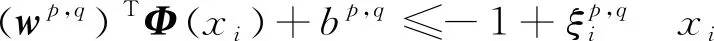
3 仿真与结果分析

3.1 数据集设计

本文基于实验室CBTC列控系统仿真平台采集多源异构数据。CBTC列控系统属于物理信息系统(Cyber-Physical System，CPS)，其数据结构设计参考文献[12]，分别从物理信息系统的物理层(Physical Layer，PL)和网络层(Network Layer，NL)采集数据，组成多源异构数据集。

物理层数据通过SNMP通信协议获得，包括ATS设备、ZC设备、CI设备、VOBC设备和网络设备的峰值CPU占用率、平均CPU占用率、峰值内存使用率和平均内存使用率。列控系统物理层信息统计量见表1。

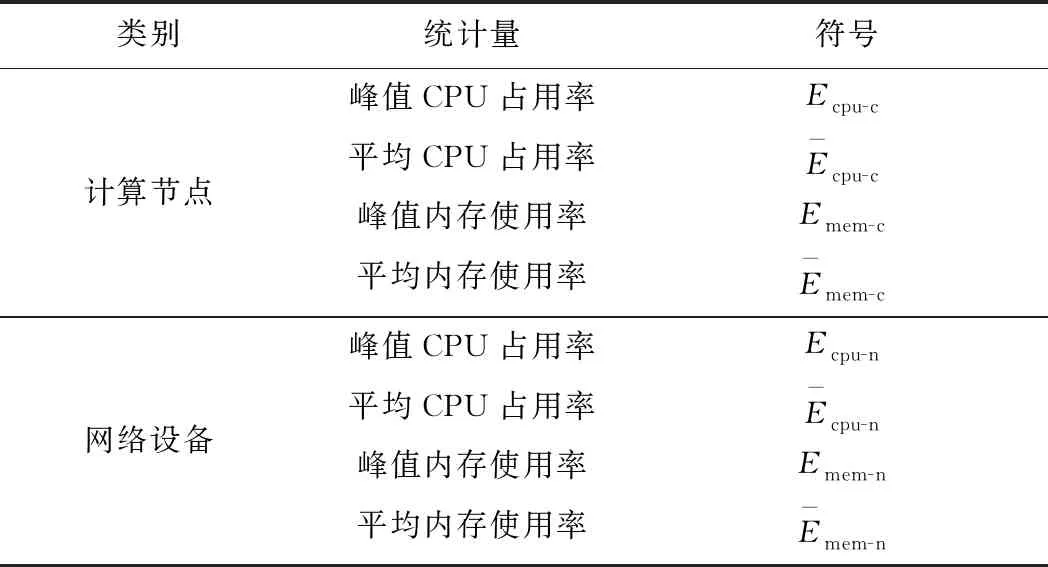
表1 列控系统物理层信息统计量

网络层数据主要采集设备集中站内部和设备集中站与列车之间的源Mac地址、源IP地址、通信会话建立(源IP与目的IP)、传输数据包(源地址与目的地址间TCP/UDP数据包)4组参数，并对这4组参数运用一维和二维统计公式进行分析计算。列控系统网络层信息统计量见表2。

表2 列控系统网络层信息统计量

表2中：S={d1,d2,…} 为数据流，且di∈R；N,LS,SS分别为数据流数目、线性和、平方和；SRi,j为数据流Si和Sj的残差之积。在单个时间窗W提取21个特征属性，共选取W=100 ms、500 ms、1 s、10 s、30 s，5个时间窗合计105个统计特征作为网络层特征属性。

数据集A可以表示为如下结构：包括2台ATS设备、4台ZC设备、4台CI设备、2台VOBC设备、6台网络设备的72个物理层特征属性集合和105个网络层特征属性集合。再通过2.1节所述方法，得到降维后多源异构数据集Ak。

3.2 仿真实验

为了验证列控系统态势感知技术效能，本文设计引入列控系统常见的Dos拒绝服务攻击和Probe端口扫描攻击。通过3.1节所述物理层、网络层多源异构数据集，完成系统态势感知，识别潜在风险。

实验采集20 000条数据用作数据集。为提高分类精度，对正常状态Normal数据集进行欠采样，并标记为类别0；对Dos攻击和Porbe攻击数据集进行过采样，并分别标记为类别1和类别2。三类数据以大致1∶1∶1的比例组成多源异构数据集，其中2/3比例用作训练集，1/3比例用作测试集。

3.3 性能指标

本文利用混淆矩阵列出正确分类与错误分类的计数值，混淆矩阵见图3。

图3 混淆矩阵

通过混淆矩阵，可以得到如下指标：TP-Ture Positive(样本为正态，预测为正态)，FP-False Positive(样本为异态，预测为正态)，TN-Ture Negative(样本为异态，预测为异态)，FN-False Negative(样本为正态，预测为异态)，则

精度Accuracy为

(19)

正确率Precision为

(20)

召回率Recall为

(21)

F1分数为正确率和召回率的调和平均，即

(22)

接受者操作特征曲线(Receiver Operating Characteristic Curve，ROC曲线)是反映召回率和误报率的综合指标。ROC曲线见图4。图4中，纵坐标为召回率，其定义见式(21)；横坐标为误报率FPR，即

(23)

ROC曲线下面积即为Area Under the Curve(AUC)。通常，AUC面积area接近1，表示分类器性能越优异。

SVD Entropy与SVM联合算法，与朴素SVM算法的仿真结果比较见表3。由表3可知，在保持精度和F1分数基本不变的情况下，SVD Entropy与SVM联合算法能有效缩短实现列控系统态势感知数据集分类的运算时间。

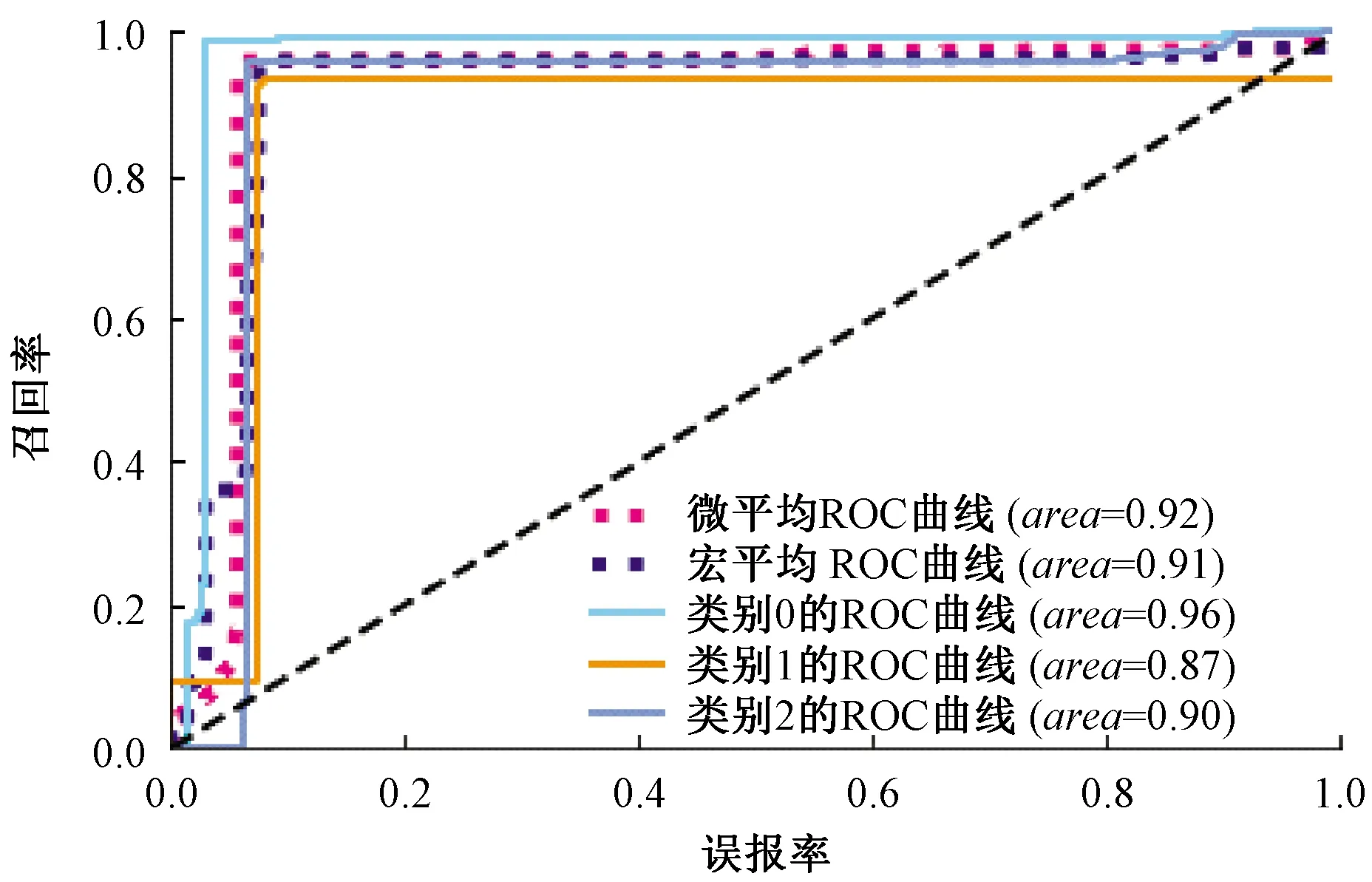
图4 ROC曲线

表3 SVD Entropy与SVM联合算法与朴素SVM算法比较

SVD Entropy与SVM联合算法，对于不同奇异值熵阈值的性能比较见表4。随着奇异值熵阈值降低，分类精度下降，对列控系统态势感知数据集的分类性能随之下降。因此，奇异值熵阈值不易选择过小，避免特征提取后的多源异构数据集Ak无法准确表达原集A的信息量。同时，选择过大的阈值，无法快速压缩运算时间。在保持分类精度基本不变的前提下，本文认为选取阈值为0.85时，是合理的阈值门限。

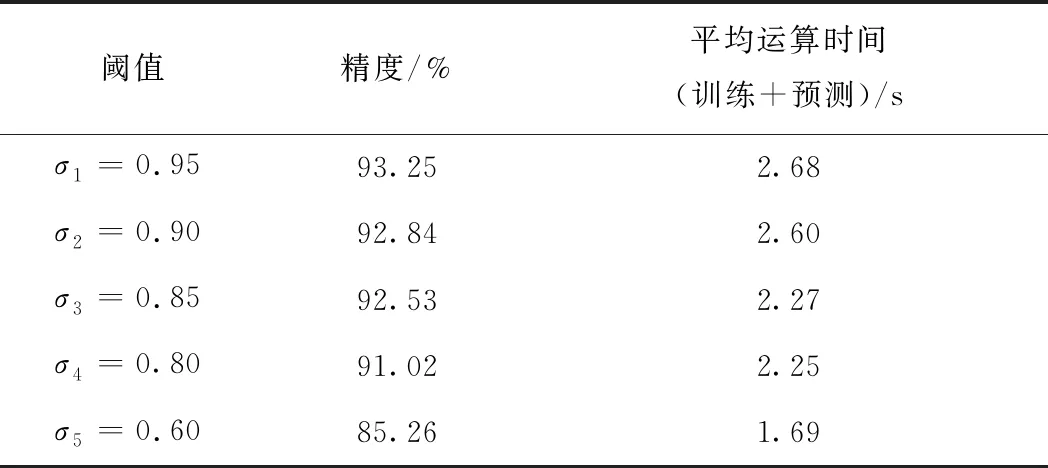
表4 不同奇异值熵阈值比较

SVD Entropy与SVM联合算法，与K近邻算法KNN[13]、朴素贝叶斯分类NBM[14]、随机森林RF[15]等分类算法比较见表5。从表5可以看出，本文提出的SVD Entropy与SVM联合算法，在保持数据分类精度基本不变前提下，运算时间较短，对于列控系统多源异构数据集的分类效果较好。

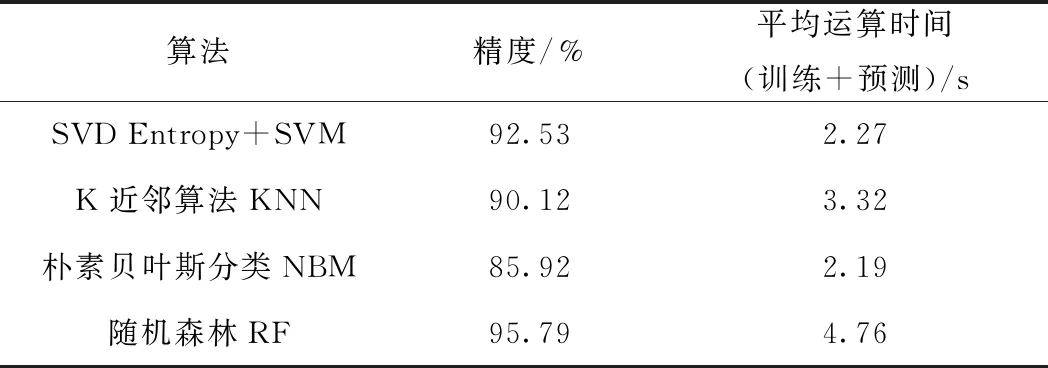
表5 不同算法比较

4 结论

(1)本文提出的SVD Entropy与SVM联合算法，通过设定奇异值熵阈值，实现了多源异构数据的快速降维。结合支持向量机多分类技术，在保持分类精度基本不变的前提下，能有效降低运算时间。仿真实验表明，当阈值设定为0.85时，为较为理想的阈值门限。通过和其他数据分类算法对比分析可知，本文提出的SVD Entropy与SVM联合算法具有较好的准确性和时效性。

(2)本文提出的联合算法，能够实现列控系统数据特征提取与分类，并快速准确识别潜在攻击和信息安全风险，为后续实时在线处理数据，进一步完成列控系统态势评价、预测提供理论支持。且本文提出的联合算法，对于高速铁路列控系统态势感知研究亦有借鉴意义。