轨道交通制动系统速度传感器的故障诊断方法研究

鲁进军，吴萌岭，牛 刚

(1.同济大学 铁道与城市轨道交通研究院，上海 201804；2.南京中车浦镇海泰制动设备有限公司，江苏 南京 211800)

轨道交通制动系统根据速度传感器采集的列车轴端速度，实现车辆的制动施加和防滑控制，速度传感器输出信号是否准确直接影响列车的安全运营。由于列车运行环境复杂，运行过程中列车振动及电磁干扰等因素的存在，造成速度传感器的输出信号发生故障，现运营的动车组中，已发生多起由于速度传感器故障，导致制动系统根据滑行判据误检测出轴抱死故障，造成列车运营晚点[1]。因此，开展速度传感器故障诊断方法的研究对保证列车的安全运营具有重要意义。

为解决上述问题，研究人员开展了列车轴抱死故障原因分析，并进行了速度传感器故障诊断方法的探索性研究。文献[2-4]分析CRH2、CRH3、CRH380BL系列动车组轴抱死故障大多为速度传感器故障造成，提出取消传感器安装支架，采用双通道速度传感器等维护措施，提升了速度传感器的可靠性，但速度传感器的故障识别还依赖人工经验线下判断。文献[5]提出基于卡尔曼滤波的信息融合估计的单、多速度传感器故障诊断方法；文献[6-7]提出基于经向基神经网络的机车、地铁速度传感器故障诊断方法；文献[8]提出基于加权K近邻分类器的机车速度传感器线下故障诊断方法。这些研究实现了线下故障检测功能，均较人工故障诊断方式提高了效率。

此外，主元分析(Principal Component Analysis, PCA)[9-13]法，为多元统计分析的常用方法，其算法简单，通过对系统正常运行产生的高维数据进行降维处理、数据特征提取、主元模型建立，实现系统异常监控和故障诊断，文献[14-15]运用主元分析法结合重构贡献图分析(Reconstruction-Based Contribution Plots，RBCP)法，实现了故障的检测与定位；但运用主元分析方法时，传统2种监控统计量可能会得到不同的检测结果，需对监控统计量进行统一化处理；牛刚等[16]提出一种基于改进主元分析法(IPCA)和改进重构贡献图法(IRBCP)的高速列车双通道速度传感器故障检测与隔离方法，对传统统计量SPE进一步细化并作为监控统计量。

表1 基于系统功能的速度传感器失效模式分析结果

速度传感器在运用过程中，会出现虚接、干扰、短路等众多故障模式，每种故障均有不同的维护方式和安全导向措施。但现运营动车组的速度传感器发生故障后，制动系统未能准确识别出断线故障，误诊为轴抱死故障，导致车辆的安全导向措施误用，因此，实现故障类型的实时智能诊断，才能从根本上解决该问题。而现有研究都主要集中在故障的检测与隔离方法，对故障类型的诊断研究较少。基于Petri网的故障诊断技术，被广泛用来表达故障系统中故障演变传递的逻辑关系，能有效地监控系统行为，若结合系统的工程运用经验，可实现故障变量的具体故障类型识别，已在锂电池、离心式压缩机等的故障诊断[17]中得到运用。

为此，本文提出一种轨道交通制动系统速度传感器的实时状态监测、故障定位与故障类型智能诊断的一体化方法；基于传统主元分析法，提出综合监控指标，解决了2种统计量监视结果不同的问题，并实现速度传感器故障发生时刻的检测；采用重构贡献图分析法，实现故障速度传感器的准确定位；并利用基于Petri网的故障诊断技术，结合速度传感器的故障模式分析和工程运用经验，建立故障演变传递的逻辑关系，实现具体故障类型的智能诊断。同时，开展速度传感器各种故障的注入模拟试验，并验证了本文方法的有效性，解决了动车组运营问题，提高了速度传感器的可维护性和安全性。

1 速度传感器故障分析

1.1 工作原理

制动系统采用开关型霍尔速度传感器，安装在装有齿轮盘的车轮轴端，当车轮旋转时，旋转齿轮将改变速度传感器前端周围的气隙磁场，速度传感器输出低电流为7 mA、高电流为14 mA的脉冲频率信号，系统的工作原理见图1。电子制动控制单元根据4个轴的速度频率信号、制动指令、车重等输入，计算本节车所需施加的制动力和监控车辆各轴是否发生滑行，并驱动气动制动控制单元及防滑阀产生制动压力，基础制动装置再根据制动压力推动制动闸瓦与车轮摩擦从而产生制动。因此，为提高系统的安全性和可靠性，需对速度传感器、气动制动控制单元、电子制动控制单元等关键部件实现故障诊断功能，本文仅介绍速度传感器的故障诊断研究。

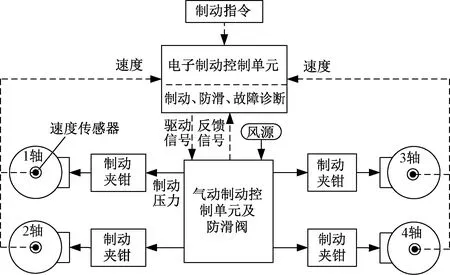
图1 制动系统工作原理

1.2 故障模式分析

从制动系统功能的角度出发，结合速度传感器的运用经验，对速度传感器的失效模式进行了分析，分析结果见表1。本文主要研究实现这些典型故障的智能诊断。

2 速度传感器故障诊断方法

速度传感器的故障诊断过程见图2，分为故障检测、故障定位和故障类型诊断3步。

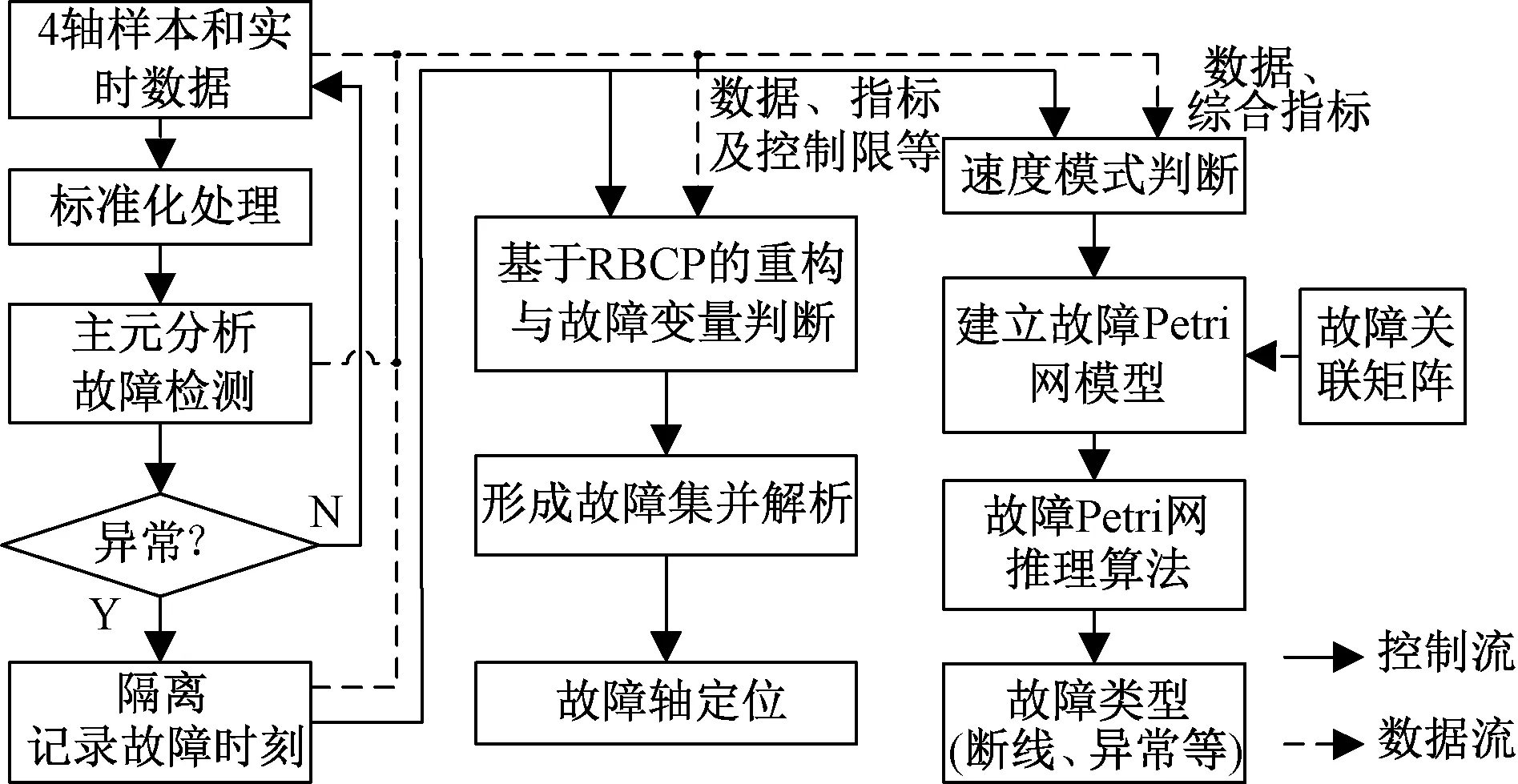
图2 速度传感器故障诊断流程图

2.1 故障检测

故障检测是故障诊断的第一步，在利用主元分析模型进行故障检测时，常用平方预测误差和Hotelling’sT2来检测系统是否发生故障，但这2种监视统计量的量度不同，容易造成监视结果不一致，因此提出一种采用T2和SPE的综合指标φ来实现故障的检测。

轨道车辆1节车有4根轴，同一时刻、同1节车的4个轴速度存在一定关联性，将4个轴的速度整体作为检测数据，并选取各轴两两间的速度残差作为观察变量，则样本表示为

(1)

式中：X为观察变量;x1、x2、x3、x4、x5、x6为6个具体观察变量;vaxle1、vaxle2、vaxle3、vaxle4分别为1节车4个轴的速度数据。

(2)

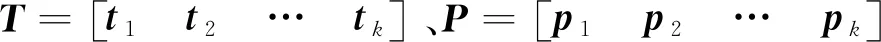
统计量SPE的定义为

(3)

统计量T2为

(4)

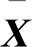
为避免统计量SPE和T2的值不同，造成检测结果不一致的缺点，提出综合指标φ，其计算公式为

(5)

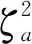
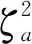
(6)

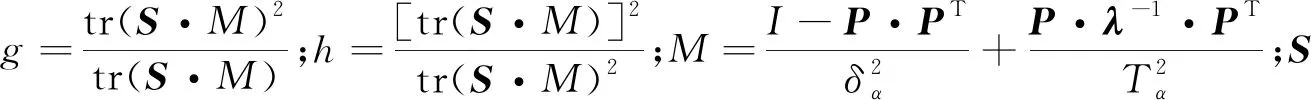
因此，基于主元分析法的故障检测时，将检测样本带入上述的统计量计算公式，得到综合指标φ，并与训练样本计算出的控制限比较，实时检测速度传感器运行过程有无故障，当有故障发生时，记录故障发生的时刻。

2.2 故障定位

通过主元分析法，能检测出故障发生的时刻，但还无法判断具体是哪个轴的速度传感器发生了故障，因此运用重构贡献图法进行故障轴定位，该方法可适用于有多个变量同时发生故障的情况。

运用重构贡献图故障定位时，不需提前考虑故障变量的个数，同时为消除对非故障变量的影响，避免拖尾效应，只对故障发生时刻内测试样本的各变量数据求重构贡献RBC值，统计故障时刻内各变量数据的RBC最大值的次数，次数最多的变量就为故障变量，从而实现一个故障变量的定位，并判断重构样本的监视指标是否超控制限，通过这样反复迭代判断，直到样本的重构指标均低于控制限为止，从而实现多个故障变量的逐个定位。

因此，基于重构贡献图的故障定位主要步骤为：

Step1定义故障变量集合Xf，初始为空集，故障变量个数k，初始默认为0。

Step2针对故障发生时刻内的测试样本数据，计算故障变量集Xf和非故障变量xi(i=1,2,…,m-k)的重构贡献RBC值，求最大值，故障发生时刻内，最大值次数最多的变量为故障变量，将故障变量加入Xf，重构贡献RBC值的计算公式为

(7)

式中：ξ为故障方向构成的单位矩阵；fi=(ξiTMξi)-1ξiTMxi为故障变量的故障幅值。

Step3故障变量个数：k=k+1。计算故障变量集合Xf的重构样本监视指标Index(xi)，并判断是否小于控制限，若满足则完成定位；否则返回Step2，继续循环定位，重构样本的监视指标公式为

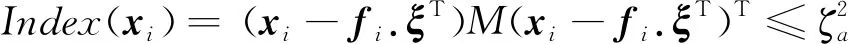
(8)

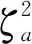
Step4通过反复循环迭代，直至故障变量集合Xf的重构样本监视指标都低于控制限，则故障完全定位。

Step5根据故障变量集合Xf，解析出具体第几轴速度传感器存在故障。

2.3 故障类型诊断

2.3.1 Petri网理论

Petri网一般由库所、变迁和有向弧三个基本要素组成，托肯(token)表征其所在库所中的资源数量。如图3所示，库所p1、p2、p3用圆圈表征，变迁t用竖条线表征，有向弧用有向线段表示，库所中的黑点则表征托肯。

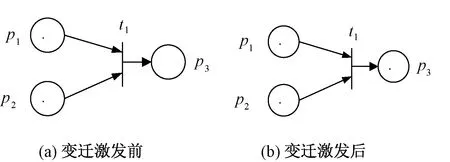
图3 故障Petri网激发模式

变迁t所有的输入库所p1和p2中均拥有一个token，满足变迁的激发规则，变迁激发后，输入库所p1和p2减少与权值对应的token个数，输出库所p3则增加相应的token个数。

设库所集合M={p1,p2,…,pn}，变迁激发集合U={t1,t2,…,tm}，系统关联矩阵C=[cij]=[W(tj,pi)]，则通过以下公式循环运算，若输出库所的标识为1，则表示故障已出现，从而实现了故障的诊断。

Mk+1=Mk⊕(C⊗U)

(9)

2.3.2 故障类型诊断

表2 速度信号模式及判断条件

同时，识别4种速度信号模式间的转换状态，并将该7种转换状态定义为初始无关故障的库所p1,p2,p3,p4,p5,p6,p7，其定义规则见表3。

表3 库所与速度信号模式转换关系规则

因此，根据1.2节中速度传感器在各种故障类型下的速度信号表现形式，结合现车运用经验，总结出速度传感器各故障发生时存在的状态转换过程，见表4，并将该5种故障定义为系统的故障库所p8,p9,p10,p11,p12。

其中，TPij为各库所间的时间约束，如TP13>50表示库所p3与p1发生的时间间隔大于50个采样点，可防止因信号抖动等干扰影响而导致误诊，各时间约束条件可伴随该故障诊断方法的工程运用而不断优化，另外异常故障包括虚接和干扰等故障。

根据表4建立速度传感器的故障Petri网模型，见图4。

表4 故障与状态转换关系表

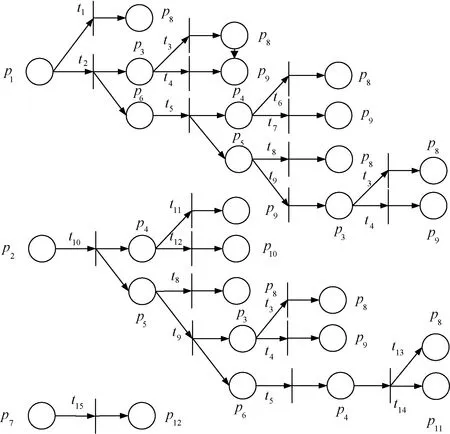
图4 速度传感器的故障Petri网模型

由故障Petri网可知，库所集合为M={p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,p12}，变迁激发的集合为U={t1,t2,t3,t4,t5,t6,t7,t8,t9,t10,t11,t12,,t13,t14,t15}。按照图5中各库所和变迁间的连接关系，得到该Petri网的关联矩阵C为

(10)

变迁的激发规则除了需要对应的库所含有token，还需要考虑时间约束问题。由式(10)和表4分析出各变迁ti的激发规则，见表5。

表5 各变迁的激发规则

因此，基于故障Petri网模型的速度传感器故障诊断时，根据被测样本的综合指标φ和速度数据，确定各故障的转换状态，形成初始库所M0，若基于时间约束的变迁激发集合U满足时，运用公式Mk+1=Mk⊕(C⊗U)，若库所M中故障模式为1时，表明速度传感器故障已出现，反之则标志着故障未形成。

3 算法验证

3.1 样本数据获取

为对故障诊断算法充分验证，需要获得速度传感器各种故障模式下的样本数据；由于速度传感器的现车实测数据无法覆盖所有故障模式，因此搭建了速度传感器试验环境，开展速度传感器各类故障的注入模拟试验。具体模拟试验类型和实现方式见表6。另外，正常、滑行和轴抱死等工况也采用了现车实测数据。

控制措施:①管道坡口加工必须符合规范要求，焊前要严格清除母材和焊道表面污物和杂质。②选用适宜的焊接电流和焊接速度，严格执行工程制定的焊接。③采用正确的焊条角度，保证焊缝两侧金属熔化结合良好。④控制错边量。

表6 速度传感器故障模拟试验列表

部分试验环境见图5，其中图5(a)为常温环境下的模拟试验，通过调速电机带动测速齿轮模拟4轴速度信号，速度传感器的速度信号经调理电路调理后，利用数据采集设备进行数据采集；图5(b)为运用振动试验台进行振动，并同时采用热风枪对速度传感器进行局部加热的模拟试验；图5(c)为速度传感器试验工装置于高温箱中的高温试验；图5(d)为浪涌试验模拟环境。

图5 速度传感器故障模拟试验

因此，结合模拟试验和现车实测数据，共获得了128组典型的速度传感器样本数据。其中，图6为正常工况下的数据曲线，4个轴的速度基本同时由225 km/h逐步降到160 km/h，数据采集周期为10 ms。

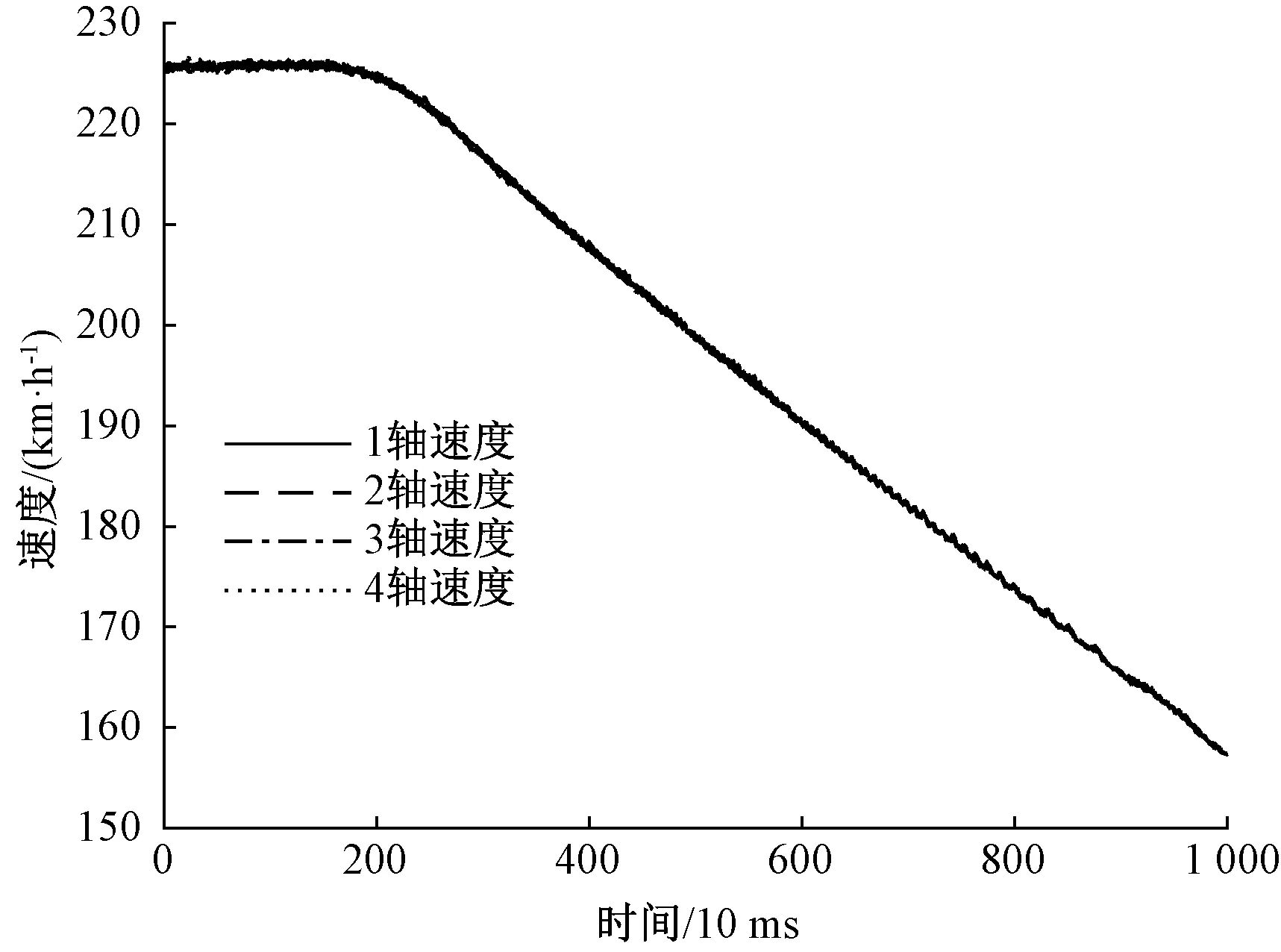
图6 正常工况下的4个轴速度曲线

图7为3轴发生断线故障的数据曲线，3轴的速度在1.2 s时突然降为0。

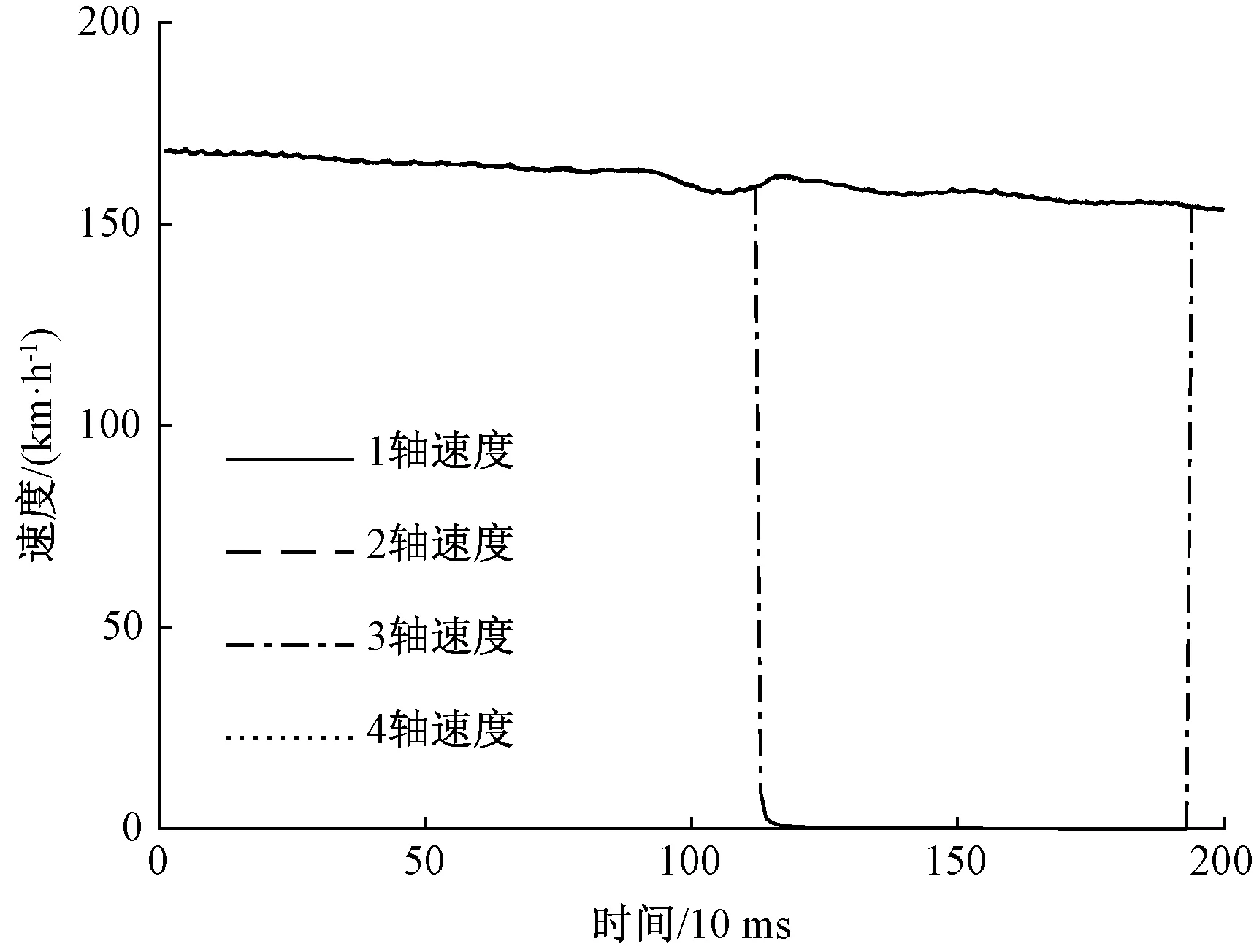
图7 断线故障下的4个轴速度曲线

3.2 算法验证

运用Matlab实现了速度传感器故障诊断方法，并运用样本数据对模型进行了训练和验证，证明了该故障诊断算法的准确性和有效性。以图7的速度传感器断线故障诊断为例，其诊断结果如下。

3.2.1 故障检测

训练样本采用正常工况下1节车4个轴的速度传感器数据，其曲线见图6； 经模型运算得到训练样本的关键参数见表7。

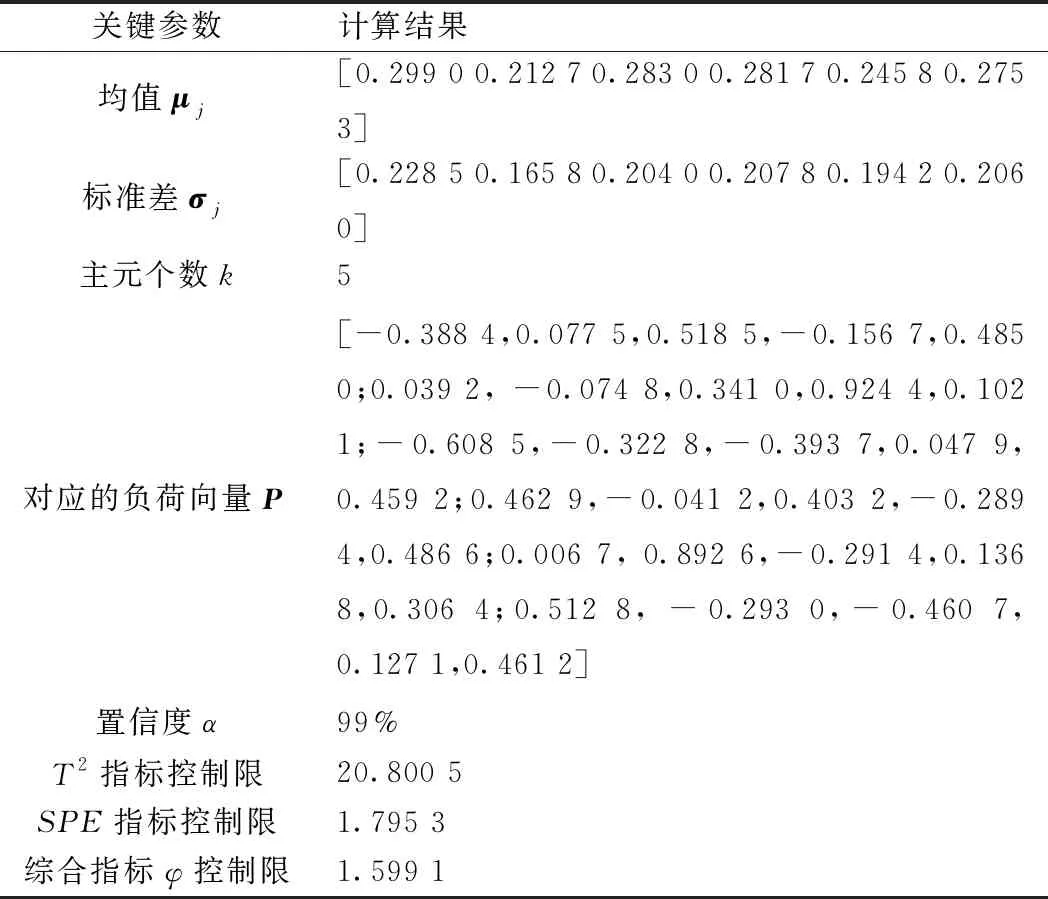
表7 训练样本的关键参数表

故障检测时，同样先对检测样本4个轴的速度进行两两求残差，得到6组变量。再根据训练样本的关键参数，实时计算出被测样本的综合指标φ，见图8。由训练样本得到综合指标φ的控制限值为1.599 1，而时刻区间0.54, 0.77,1.13～1.93 s时，被测样本的综合指标φ值超过控制限，表明此时有故障发生，从而实现了故障的检测，并记录故障发生的时刻区间。

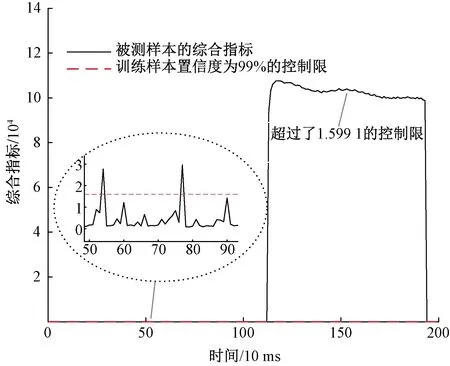
图8 测试样本的综合指标曲线

3.2.2 故障定位

故障轴定位时，在已检测出的故障时刻区间0.54, 0.77,1.13～1.93 s内，计算每个时刻6个变量的重构贡献RBC值，RBC最大值对应的变量就为故障发生的变量，统计各变量被定位为故障的次数，见图9(a)，第1次定位诊断时，6个变量被定位为故障的次数分别为1、81、1、0、0和0，被定位为故障次数最多的变量就为故障变量，因此此时故障变量集为Xf={2}，从而实现第1个故障变量的定位。

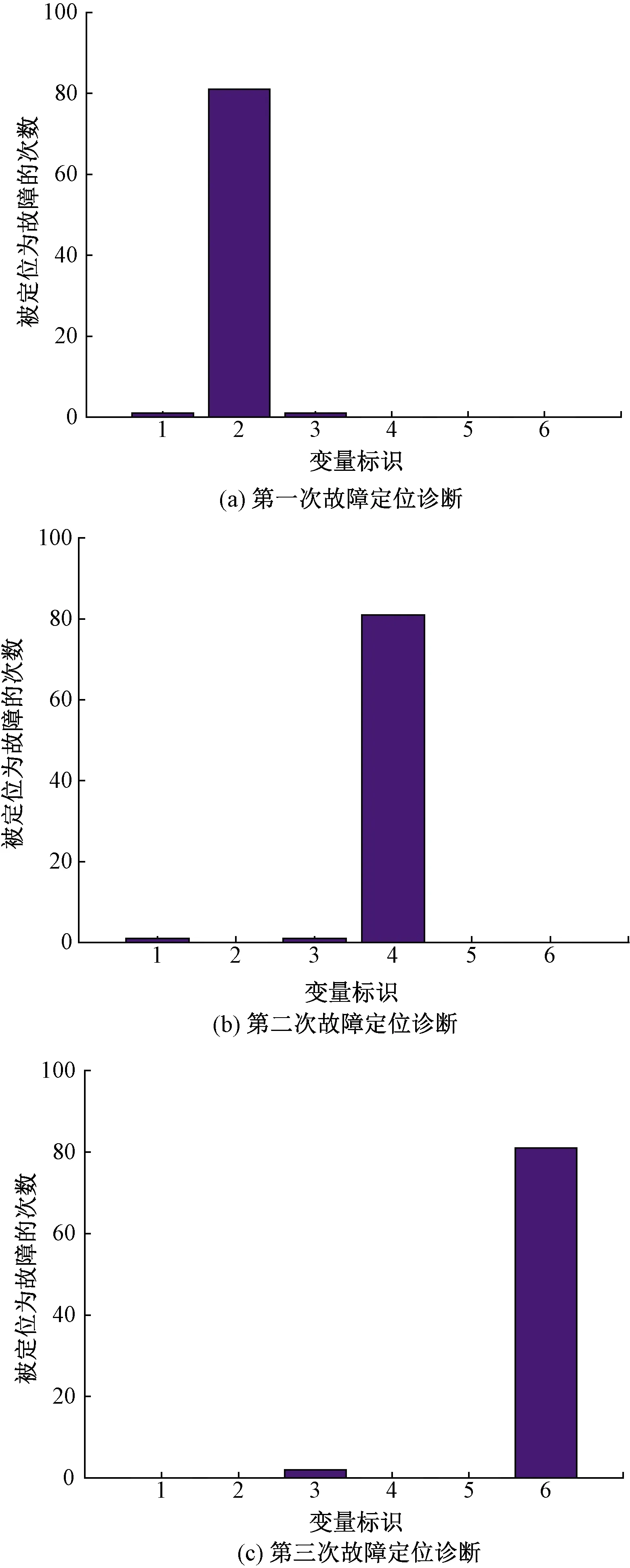
图9 6个变量的故障数柱状图

每定位出1个变量后，计算重构样本的监视指标并判断是否超控制限φ，见图10。控制限值为1.599 1，第一次重构后，时刻区间0.54, 0.77, 1.13～1.93 s的重构样本监视指标均超控制限，因此需继续进行RBC值计算和故障变量判断，经3次迭代判断后所有重构样本的监视指标均小于控制限，故障定位结束，所有的故障变量已均被定位出来。因此，由图9可知，故障变量集为Xf={2,4,6}，并利用组合最大化思想和各变量与轴的关系，推导出故障轴为3轴，实现了故障轴的准确定位。

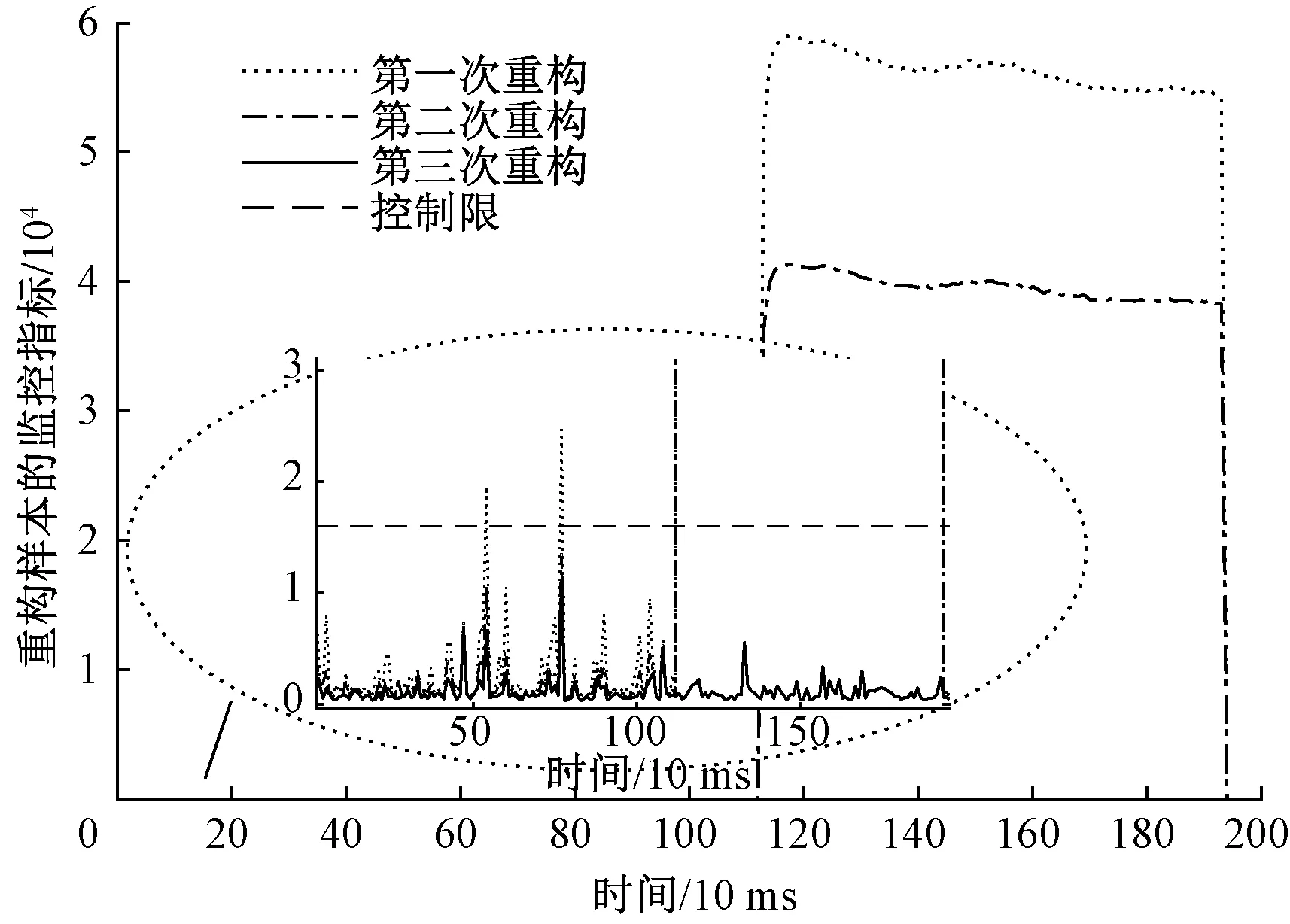
图10 测试样本的重构监控指标曲线

3.2.3 故障类型诊断

故障具体类型诊断时，根据表2，得到速度信号的模式图，见图11。在时刻0.54 s和0.77 s时，瞬时速度信号模式为1，说明此时速度信号异常但不为0；1.13～1.93 s时，瞬时速度信号模式为2，说明此时速度信号异常且速度小于1 km/h，从而得到该检测样本的速度信号模式的转换状态过程，见图12；同时为了便于描述诊断过程和结果，绘制了该故障诊断过程的Petri网，见图13。

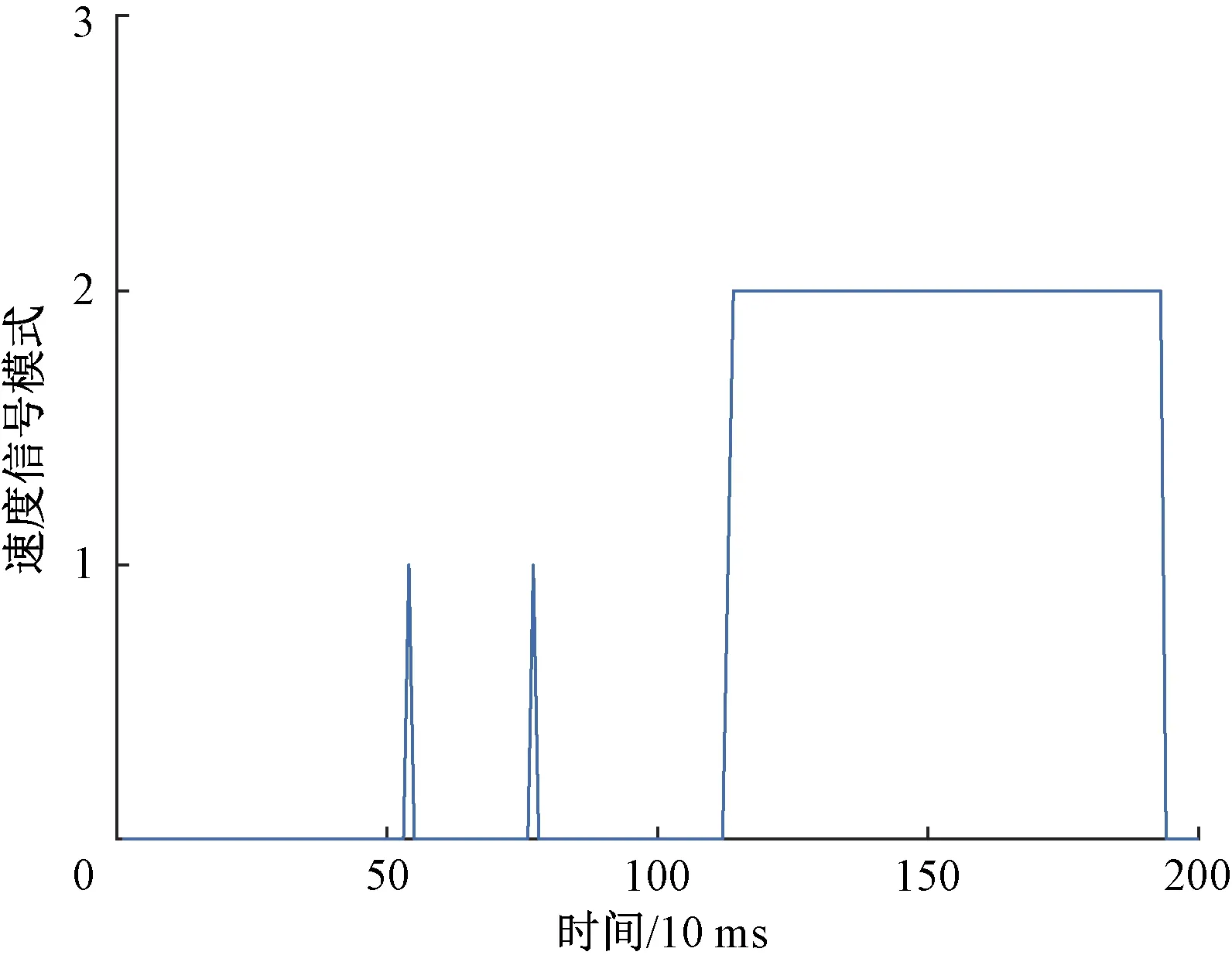
图11 故障轴的速度信号模式图

由图12可知，时刻0.54 s时，p2=1，则变迁条件t10=1，诊断算法通过方程Mk+1=Mk⊕(C⊗U)得到库所p2、p4、p5，但此后p8,p9,p10,p11,p12对应的激发条件均无法满足，因此不存在故障，其诊断过程见图13中的绿色部分，0.77 s时刻也同样不存在故障。

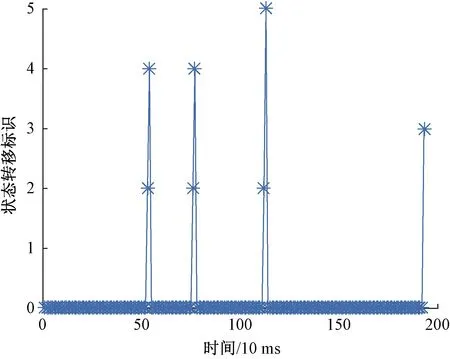
图12 故障状态变化过程

时刻1.13 s时，p2=1，则变迁条件t10=1，运用状态方程Mk+1=Mk⊕(C⊗U)得到库所p2、p4、p5，实时判定变迁激发条件是否满足，继续得到相应的变迁激发序列U，直至可判定故障类型的库所p8,p9,p10,p11,p12中存在点(点表示token)，则一次故障诊断结束，其诊断过程见图13中的绿色和红色部分，因此最终结果为M=[0 1 1 1 1 1 0 1 0 0 0 0]T，p8为1，诊断出为断线故障。

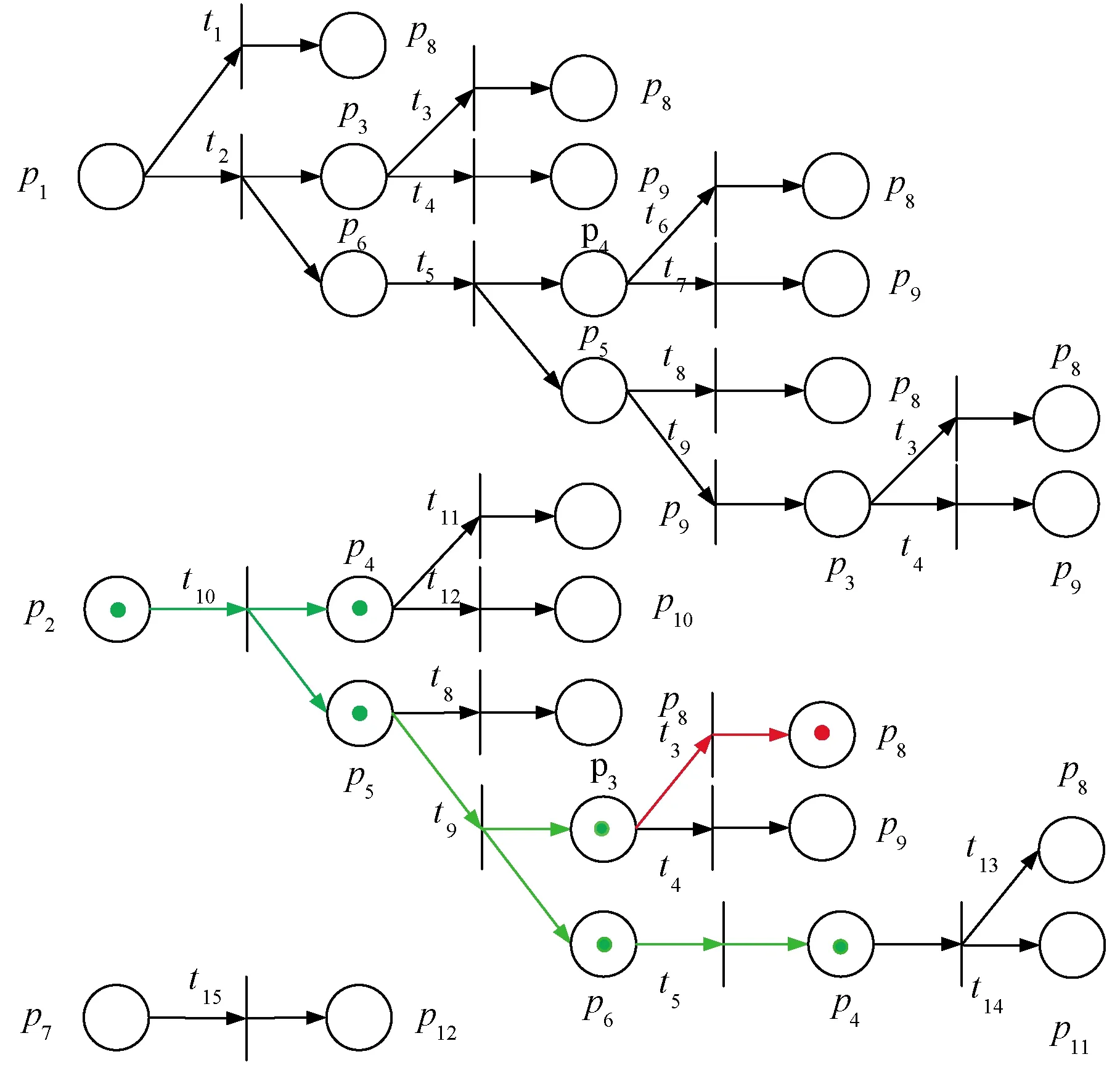
图13 断线故障的Petri网

因此该检测样本的诊断结果为：3轴速度传感器在1.13～1.93 s时刻发生了断线故障。

通过验证，证明了该诊断方法的有效性，同时现有的制动系统遇到这种速度传感器的断线故障时，将会误报出轴抱死故障，若将该诊断方法运用于制动系统工程化产品，能有效解决现车存在的误报问题，提高系统的安全性。

4 结论

本文提出一种轨道交通制动系统速度传感器故障的一体化智能诊断方法，实现了速度传感器故障发生的实时检测、具体故障轴的准确定位、故障类型的自动识别。

(1)基于主元分析法，通过检测样本的1种综合监控指标是否超限判断，实现速度传感器故障的实时检测，有效避免了传统主元分析监控指标量度不同造成检测结果不一致的缺陷。

(2)采用重构贡献图故障定位方法，通过反复迭代判断，实现具体故障轴的准确定位，可用于多变量故障的定位，并减小了对非故障变量的影响，避免拖尾效应。

(3)在速度传感器故障模式分析的基础上，基于Petri网的故障诊断技术，结合工程经验，建立了各故障演变传递的逻辑关系，实现速度传感器典型故障的自动识别。

(4)结合速度传感器的现车运营数据和故障注入模拟试验数据，对诊断算法进行训练和验证，并以速度传感器断线故障的诊断过程和结果为例，证明了该故障诊断方法的有效性，解决了现车的误报隐患问题，也为速度传感器典型故障的安全导向措施研究与实施奠定了基础。