基于滑模控制的孤岛直流微电网控制策略研究
梁海峰,边 吉,丁锦睿,李 鹏
(华北电力大学 河北省分布式储能与微网重点实验室,河北 保定 071003)
0 引 言
微电网作为整合分布式发电装置、储能系统以及各种负载的灵活载体,受到了诸多研究人员的高度重视。与交流微电网相比,直流微电网具有更高的能量转换效率,同时不必考虑系统的无功缺额问题,间接减少了搭建成本[1]。
针对孤岛直流微电网,因其缺少主网功率支撑,为了保证其在各种负荷需求条件下的安全运行,有必要考虑恒功率负载(Constant Power Loads, CPL)的大量接入导致其稳定性的退化问题。为解决此问题,诸多学者从系统建模、控制策略以及稳定性分析等多种角度对其进行研究。
文献[2,3]从阻尼控制的角度入手,重塑负荷侧输入阻抗或微源侧输出阻抗,改善系统的稳定性。但是其局限性在于需要详细的系统参数以建立准确的闭环传递函数,一旦系统参数随环境等因素引起变动,所增设控制环节的补偿效果将变差。因此,越来越多的非线性控制方法应用至微电网的研究中去,其中滑模控制(Sliding Mode Control, SMC)以其对系统参数变化的不敏感性而逐步被应用到变流器的控制中去[4-7]。
目前,研究者更倾向于以单微源为CPL供电为研究主体,运用SMC对变流器进行控制。文献[5]为变流器设计了底层滑模控制器,证明了基于线性开关面的滑模控制器能够弱化CPL对系统稳定性的影响。文献[6]以两级Boost变流器为CPL供电为例,采用自适应全局滑模控制保证系统的稳定性。文献[7]将自适应控制与滑模控制相结合,文献[8]将反馈线性化与滑模控制相结合,均使系统的鲁棒性和稳定性得到提高。但是上述研究的不足之处在于仅考虑单个微源供电或将多个供电微源等效成一个微源,当多个微源并联供电时,无法用上述控制策略为每个变流器设置滑模控制器。文献[9]虽然为每个并联供电的变流器设计了滑模控制器,但是仅考虑了阻性负载,因而无法证明在CPL接入后的控制效果;文献[10]针对并联供电的光伏出口变流器和储能变流器分别设置了滑模控制器。但是,文献[9,10]的不足之处在于没有考虑线路电阻的影响,这使得母线电压的动态特性与变流器电容电压的动态特性一致,虽然便于母线电压的稳定性分析,但是显然这种等效简化并不合适。
除上述从稳定性的角度出发提出各种控制方法外,诸多学者针对微源间的功率精确分配进行了研究,文献[11,12]针对传统下垂控制提出了各种二次控制措施,提升了微源间的功率分配精度。
基于上述分析,针对微源出口变流器,本文首先提出一种适用于滑模控制的微源电感电流参考值选取方案,并结合抛物线型下垂控制共同实现了微源的功率精确分配以及供电质量的提升。随后,对各变流器设计了一种基于定频PWM的滑模控制器,与基于传统下垂控制的双环控制方式相比,此方法能够得到恒功率负荷比例与滑模控制参数之间的关系,以保证微网能够接入更高比例的恒功率负载。最后,通过MATLAB/Simulink进行仿真分析,对所提控制策略的有效性进行验证。
1 微电网系统模型
图1为直流微电网简化模型,其中负荷包括阻性负荷和恒功率负荷,后者端电压受到负荷点(Point-of-Load, POL)变流器严格控制。对于采用最大功率点跟踪(Maximum Power Point Tracking, MPPT)控制的微源,其外特性与恒功率负载特性相似,建模时将其视为输出功率为负值的恒功率负载[13]。本文将恒功率负荷消耗功率和上述类型的微源提供的功率合并为等效恒功率负载,记为PCPL。另外,考虑到低压微电网线路电阻参数大于电感参数,因而建模时仅考虑线路电阻Rli。

图1 直流微电网系统简化模型
图1中,vsi和vCi分别为微源初始电压和变流器出口电压;Li和Ci为变流器电感和电容。变流器电感电流记为iLi,微源输出电流记为ioi,母线电压记为vbus,负荷总电流记为iload,阻性负载电阻用R表示。
针对任意第j个微源,当其向外供电时,存在以下方程:
(1)

vCj=Rlj·ioj+vbus
(2)
混合负载吸收的瞬时电流为
(3)
考虑到负荷平衡,有以下关系式成立:
(4)
式中:ξj表示微源j的供电比例。
2 下垂控制与功率精确分配方案
2.1 下垂控制
当各微源采用传统线性下垂控制时,为防止母线电压过低,人为设定阈值d,在正常运行时应满足vbus>(1-d)vN,vN为母线电压额定值,d一般选择为0.05[14]。
图2为微源j的线性及抛物线型下垂控制曲线对比图,Rj为下垂系数Rvj与线路电阻Rlj之和。将微源j的最大输出功率记为PBj,当母线电压处于临界值(1-d)vN时,其输出的最大电流为

图2 线性及抛物线型下垂控制曲线
(5)
(6)
由图2可见,这种凸函数的优势在于,在相同的供电电流下,抛物线型下垂曲线能使母线电压产生更小的电压降落(电压增量为Δvj)。因此,下文将传统线性下垂控制替换为抛物线型下垂控制。然而这种替换依旧无法实现微源间的功率精确分配。因此有必要提出一种功率精确分配方案以改善此问题。
2.2 功率精确分配方案
当系统处于稳定时,由式(1)可以得到各开关管Sj1的稳态占空比,将其记为Uj,大写字母表示稳态值(下同),对任意微源j,在稳态工作点处有
(7)
进而得到稳态电感电流值:
(8)
稳态下,各变流器出口电压将达到其参考电压值VCj_ref,考虑到不同变流器出口电压值与线路压降的差值总等于母线电压值Vbus,而线路压降一般比较小,因此VCj(j=1,2,……,n)彼此相差不大,由式(8)可近似认为ILj∝Ioj/Vsj。
为了实现各微源供电电流按各自容量成正比分配,而微源容量可由最大输出功率PBj反映,即在稳态时期望Ioj∝PBj,因此电感电流ILj期望有以下关系式:
(9)
式中:μj为微源j的电感电流分配系数。考虑到稳态时的电感电流ILj应等于其参考电流iLj_ref,基于此即可给出微源j的电感电流参考值为
(10)
由式(10)计算得到的电感电流参考值既反映微源自身特性又反映微电网功率需求状态。对任意微源而言,其需要接收其余微源的电感电流信息,可借助低带宽通信技术实现信息的共享。另外,考虑到电感电流的高次谐波和脉动,因此可对其先进行低通滤波,使得参考值平滑。
下面分析任意两台微源之间输出电流的分配关系。以第m台微源和第k台微源输出电流关系为例,由式(7)得到:
(11)
由式(9)可知,上式中ILm与ILk之比等于电感电流分配系数之比,因此进一步可得:
(12)
可见,利用上述方法使得各微源输出电流之比近似等于最大输出功率之比,大大提升功率分配精度。
3 滑模控制器设计
下面将以任意微源j为例,说明其滑模控制器设计原理。
3.1 滑动流形的选取、趋近律及等效控制信号
在滑模控制中,期望系统状态轨线最终达到其平衡点,将引导轨线运动的面S称为滑模面,更一般的,称为滑动流形[15]。定义滑动流形S后,可将整个轨线运动空间分为S>0和S<0两个子空间,不同子空间采用不同控制信号,进而迫使状态轨线沿着滑动流形S运动,最终使其到达平衡点,实现控制目标。

Sj=αj(vCj-vCj_ref)+βj(iLj-iLj_ref)
(13)
其中,αj和bj称为滑动系数,电容电压的误差ΔvCj和电感电流误差ΔiLj作为两个状态变量,滑模控制的目标是使得两状态变量趋于零。针对状态变量的趋近过程,选定指数趋近律[16]:
(14)
式(14)中,指数项-kjSj保证当Sj较大时具有较大的趋近速度,当轨线靠近滑动流形时自动减小趋近速度;等速趋近项-εjsgn(Sj)使轨线具有恒定速度,保证其在有限时间内能达到滑动流形。选择较小的εj以及较大的kj能够实现较快的控制响应速度同时减小滑模控制中的抖振现象。
联立式(13)和式(14),利用不变性条件可得到开关管Sj1的等效控制信号uj_eq,下文推导该信号时,由于电感电流参考值iLj_ref是各电感电流经低通滤波后按式(10)得到的,考虑到电感和滤波器的平波作用,可以认为电感电流参考值iLj_ref的微分近似为零,以下为推导过程:

(15)
式(15)中的dioj/dt可由式(1)第二个方程求微分得到,即有:
(16)

-εjsgn(Sj)-kjSj
(17)
(18)
式中:
(19)
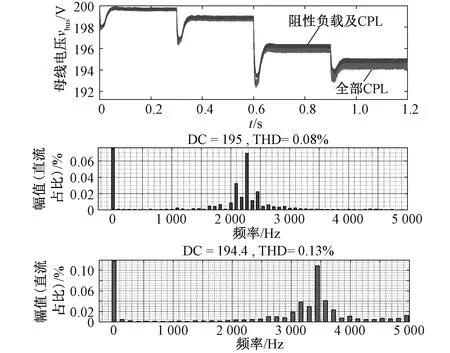
通过选取合适的控制参数,总能使控制信号uj_eq1或uj_eq2成为所需的等效控制信号。以uj_eq1为例,令0 (20) 观察式(18)中的Bj,选取较大的bj很容易使得Bj<0成立,这时为了使式(20)的第一个关系式成立,进而推得需要Dj<0成立。对于式(20)的第二个方程式,推得需要满足Bj (21) 观察式(18),适当增大bj同时减小aj以及ej总能使得式(21)成立,进而得到控制信号uj_eq=uj_eq1。将等效控制信号uj_eq与定频三角载波比较,即可将其转换为脉冲宽度调制的瞬时占空比信号[17]。图3为以微源1为例绘制的整体控制框图,其余微源控制器实现与之类似。 图3 整体控制框图 为了保证轨线能够接近并最终达到滑动流形,需要满足滑模控制的可达性,即应满足[16]: (22) 式中:τj>0。 将式(14)带入式(22)中,得到: (23) 式(23)中只要满足|Sj|(εj+kj|Sj|)>τj即可实现可达性。显然,当设定好tj后,当|Sj|大于一定阈值时总能满足可达条件,当|Sj|进一步减小时,仅可达性并不能使得轨线一直处于滑动流形的邻域范围内,因此也就引出了存在性条件[16]: (24) 由式(25)可见,以指数趋近律运动的轨线总满足上述条件: (25) 为保证轨线滑动过程中母线电压的稳定,需对其稳定性进行分析,常用的方法是在平衡点处线性化[5]或利用李雅普诺夫理论[18]进行证明,本文通过前者分析其稳定性。当轨线在滑动流形上运动时,有Sj=0成立,由式(13)得到电感电流iLj: (26) (27) (28) 将式(4)带入上式,同时考虑负载电流iload的线性近似[10],即: (29) 进一步可得到母线电压方程: (30) 式中: 当母线电压vbus工作在某一稳态工作点ρ.vN时(其中ρ>(1-d),d为阈值),对式(30)在ρ.vN附近进行线性化,即有: (31) 仅当dgj(vbus)/dvbus<0时,上述微分方程才能保持稳定。将式(30)带入上式得到: Kj3>-2Kj2ρvN (32) 因此,为保持母线电压的稳定需要满足式(32)。将系数Kj1—Kj4中负荷电流iload对母线电压vbus的微分用下式(33)替换,并用J表示。该数值的大小反映了微电网中阻性负荷和恒功率负荷的比例。 (33) 将式(30)、(33)带入式(32),得到用J表示的稳定判据方程: (34) 上述二次方程系数均为不小零的实数。根据式(34)绘制以J为自变量的曲线,如图4所示,该抛物线的对称轴为 图4 不同负荷配比下fj(J)示意图 (35) 其极小值点为 (36) 从式(34)可见,图4中抛物线的开口程度、极小值点都将随滑动系数等参数的不同而变化,进而形成一抛物线簇,当其存在零点时,将抛物线靠近纵轴的零点记为JSj。针对某一确定的工作曲线,母线电压的稳定性将取决于J的值。以曲线Mj1为例,当J>JSj时,即可保证母线电压的稳定。虽然另一个零点左侧区域也能使得fj(J)>0,但是左侧为CPL渗透率增大的方向,这与其对微电网稳定性的弱化作用不符。 另外,假设滑动系数等参数选取的极不恰当,使得微电网处于曲线Mjm上,对应JSj趋近于0—,此时使母线电压稳定的J的取值区间最小,这意味着当0 (37) 从式(37)可知,当CPL消耗的功率不大于阻性负载消耗时,总能满足稳定判据(34)。当控制参数选取合适时,能使JSj向左移动,进而扩大微电网所带CPL比例的上限。在极端情况下,当负荷均为CPL时,对应式(33)中的R→∞,此时J为有限负数,只要保证JSj位于其左侧,即可保证母线电压的稳定。 为验证所提控制策略的有效性,利用MATLAB/Simulink搭建了一个孤岛直流微电网,其结构如图5所示,其中光伏微源工作在MPPT模式,额定温度TN=25 ℃,额定辐照度Ir=1 000 W/m2,其余模型参数选取如表1所示。 图5 直流微电网仿真模型 表1 直流微电网参数 设置以下工况:t=0 s时,Ir=100 W/m2,对应PV输出功率为140 W,阻性负载R1和恒功率负载CPL1接入系统;t=0.3 s时,Ir上升至1 000 W/m2,对应PV输出功率为350 W,同时阻性负载R2接入系统;t=0.6 s时,CPL2接入系统;t=0.9 s时,CPL3接入系统,仿真步长5×10-6s。 4.2.1 相轨迹分析 以DG1为例,针对其电感电流和电容电压设置多组不同初始值,将ΔvC1和ΔiL1作为两个状态变量,仿真得到的相轨迹如图6所示。可见,处于相平面中不同初始位置的轨线1~4最终都达到了预先设定好的滑动流形上,即图中的灰色虚线,其斜率由α1和b1决定。以曲线1为例,一旦其跨入至S1>0的区域时,由式(14)可见其趋近律将发生切换,迫使轨线沿着滑动流形附近运动,其他轨线的运动与之类似,不再逐一分析。 图6 不同初始条件下的相轨迹 一旦轨线进入滑动阶段,当负荷发生投切时,其将沿着滑动流形运动,经过暂态过程,最终返回至稳态点附近。 4.2.2 性能对比 假设DG1~DG3分别采用以下三种控制策略:传统线性下垂控制、文献[12]所提改进下垂控制以及本文所提SMC控制。 图7为母线电压波形对比图,当t=0.6~0.9 s时系统均保持稳定,此时CPL的功率需求已经大于阻性负载,这意味着三种不同控制方式下的微网都具有携带一定比例CPL的能力。当t=0.9~1.2 s时,当采用传统控制方式及文献[12]所提控制方式时母线电压均出现骤降,而采用SMC时,母线电压依旧稳定。图8为利用式(34)计算得到的各微源稳定判据方程波形,可见在负荷波动时fj(J)(j=1,2,3)均大于零,因而母线电压能够保持稳定。另外,在相同的负荷接入下,采用本文所提控制策略时的母线电压降落程度最小,暂态性能最好。 图7 母线电压波形对比图 图8 各微源的稳定判据方程波形 图9为不同控制策略下各微源输出电流波形对比图,表2为t=0.6~0.9 s时供电电流对比。传统控制下,微源间功率分配存在较大的分配误差,最大分配偏差为4.48%。在文献[12]所提控制策略下,其分配精度得到提高;然而其改善效果与线路电阻测量值密切相关,由于存在测量误差,因而在实际应用中其改善效果具有局限性。采用本文所提控制策略时,最大分配偏差下降至0.93%,大大提升功率分配精度。 图9 各微源输出电流波形 表2 t=0.6~0.9 s时微源输出电流对比 采用SMC控制时,为验证微网应对纯CPL的能力,将上述混合负荷需求全部替换为CPL,对比微网为混合负载供电以及为纯CPL供电下的母线电压波形,并在t=1.18 s时对母线电压进行快速傅里叶分析(Fast Fourier Transform,FFT),仿真结果如图10所示。 图10 母线电压波形及对应的FFT分析 可见,两种工况下的总谐波失真率均在可控允许范围内,这意味着当负荷全部替换为CPL后,依旧能够保证直流母线电压的稳定。 上述仿真结果意味着式(37)是极为保守的,当滑模控制参数选取适当时,可以大幅度扩大CPL在混合负载中的比例,甚至微网内负荷均为CPL时,也能保证直流母线电压的稳定。 4.2.3 SMC的鲁棒性验证 令上述负荷波动情况和各控制参数保持不变,将各微源的变流器电容Cj或电感Lj(j=1,2,3)同时增大或减小30%,分析t=0.55~1.00 s期间的母线电压波形,仿真结果如图11所示。 图11 参数变动下的母线电压波形 由图11可见,变流器结构参数的整体增大或减小对母线电压的暂态恢复过程和稳态运行特性基本均不产生影响。可见,利用SMC控制时能够保证系统对结构参数摄动的鲁棒性。 本文针对孤岛直流微电网,兼顾稳态运行性能及稳定性,针对微源变流器提出了一种基于PWM的滑模控制策略,具体结论如下: (1)将SMC与抛物线型下垂控制相结合减小了母线电压的降落并通过对各变流器电感电流进行控制,间接实现了各微源供电电流近似按各自容量进行比例分配。 (2)针对CPL对系统稳定性造成的影响,提出一种基于定频PWM的滑模控制策略,着重分析了微电网允许接入CPL比例与滑模控制参数之间的关系,提升了系统的稳定性。 (3)搭建仿真模型,对所提控制策略对微电网稳定性、稳态运行特性的提升以及SMC的鲁棒性进行了验证。
3.2 滑模控制的可达性和存在性

3.3 滑模控制的稳定性

4 仿真验证
4.1 仿真模型及参数


4.2 仿真结果及讨论






5 结 论

