计及导向摆臂约束的重型货车驾驶室俯仰平面动力学模型*

赵雷雷，于曰伟，周长城，黄德惠，袁 建

（1.山东理工大学交通与车辆工程学院，淄博 255000；2.一汽解放青岛汽车有限公司研发部，青岛 266043）

前言

重型货车驾驶室悬置系统影响着驾驶员的舒适性和健康［1-2］。该系统的优化设计、特性分析及控制是一项非常复杂的工作［3］，这主要是由驾驶室振动的复杂性决定的［4-6］。目前，大多数重型货车的驾驶室都装有摆臂导向机构，以抑制其俯仰运动。在车辆行驶过程中驾驶室的振动响应与驾驶室悬置导向机构的约束特性直接相关。也即，由于导向机构的约束作用使得驾驶室各向振动相互耦合。

借助驾驶室系统动力学模型，把握系统振动特性，对悬置参数设计与调控和舒适性的提升等非常重要。尽管可在考虑上述耦合的情况下建立复杂三维驾驶室动力学模型，但驾驶室平面动力学模型在某些应用中效率更高［7］。其中，驾驶室俯仰平面动力学模型对驾驶室悬置系统设计与控制起着重要作用［8］。例如，车辆行驶于颠簸路况时，路面近似于多个正弦路面的叠加［9］，且驾驶室主要运动发生在俯仰平面。在此情况下，与三维驾驶室模型相比，平面动力学模型更便于研究人员快速对俯仰平面内的运动进行研究。然而，传统的驾驶室俯仰平面动力学模型，没有考虑驾驶室悬置系统导向机构的约束作用，仅能用于粗略计算驾驶室垂向运动和绕驾驶室质心的俯仰运动［10］，不能用于研究驾驶室质心纵向动力学特性和驾驶室悬置导向机构的运动特性等。事实上，在俯仰平面内驾驶室质心存在一定的纵向水平运动［11］，且驾驶员对低频范围内驾驶室的纵向振动比垂向振动更为敏感［12］。为给提高驾驶室纵向振动舒适性提供必要的理论指导和技术支撑，有必要考虑导向机构的约束作用，进而建立能够反映驾驶室真实振动响应的俯仰平面动力学模型。

此外，驾驶室悬置系统控制策略开发大多基于驾驶室系统动力学模型［13-14］。目前，因所使用的俯仰平面动力学模型精度不高，而且不能计算驾驶室质心的纵向振动分量，影响了控制策略调控性能的提升。尽管黄德惠等［3］、Wang 等［15］和王国林等［16］基于商业化动力学软件建立了复杂的驾驶室动力学仿真模型，但因没有给出动力学方程，故它们均不便用于基于模型的驾驶室悬置系统控制策略研究，这使得它们在驾驶室控制研究中的应用受到了限制［17-18］。除了基于商业化动力学软件的模型外，现有研究中鲜有文献考虑驾驶室悬置导向机构的约束作用而创建俯仰平面动力学模型并给出振动方程。可见，驾驶室俯仰平面动力学模型尚待进一步研究。

本文旨在考虑驾驶室悬置导向摆臂的约束作用，重构驾驶室俯仰平面动力学模型，从而提高模型精度，拓宽模型工程应用范围，为驾驶室悬置系统的设计与控制提供可靠的理论模型。

1 驾驶室悬置系统与俯仰平面约束

1.1 驾驶室悬置系统结构

重型货车驾驶室悬置系统的结构形式很多，本文所研究的驾驶室悬置系统目前应用最为广泛，其结构如图1所示。

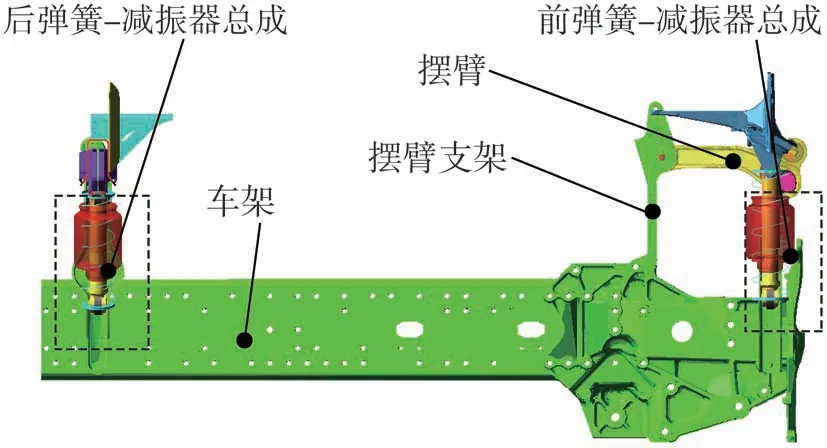
图1 驾驶室悬置系统结构示意图

由图1 可知，驾驶室悬置系统由前悬置系统和后悬置系统组成。前悬置系统主要包括前弹簧-减振器总成、导向机构（由摆臂和摆臂支架组成）；后悬置系统主要包括后弹簧-减振器总成。其中，弹簧为弹性元件，减振器为阻尼元件，导向机构主要起导向和约束驾驶室运动的作用。

1.2 驾驶室俯仰平面运动约束特性分析

图2 俯仰平面结构示意图

图2 为图1所示重型货车驾驶室悬置系统在驾驶室俯仰平面内的结构示意图。由图2 可知，驾驶室悬置系统受到车架激励时，摆臂绕其与摆臂支架的铰接点W 发生转角θ；在摆臂的约束作用下，驾驶室产生俯仰角φ，同时在纵向和垂向分别产生位移△x 和△z。此时，后减振器产生摆角△α。由此可见，在驾驶室俯仰平面内，由于摆臂的约束作用，驾驶室的俯仰运动、纵向运动及垂向运动相互耦合。

2 驾驶室俯仰平面动力学建模

2.1 物理模型

目前研究驾驶室在俯仰平面的振动与控制时，所采用模型通常不考虑驾驶室悬置导向机构的约束，仅考虑驾驶室垂向运动和绕驾驶室质心的俯仰运动，如图3（a）所示。为提高驾驶室俯仰平面动力学模型的精度，拓宽模型工程应用范围，本文中在前述驾驶室俯仰平面运动约束分析基础上，创建了考虑摆臂约束的驾驶室俯仰平面动力学模型，如图3（b）所示。

图3 驾驶室俯仰平面物理模型

图3 （b）所示模型中，除去车架外的运动构件包括：前减振器杆和筒、后减振器杆和筒、摆臂及驾驶室，共6 个。A 和A"分别为后悬置弹簧-减振器总成与驾驶室和车架的铰接点；B 和B"分别为前悬置弹簧-减振器总成与驾驶室和车架的铰接点；C 为驾驶室的质心；D 为驾驶室和摆臂的铰接点；W 为摆臂与摆臂支架的铰接点；E 为驾驶室地板上的任意一点。前减振器杆与筒之间为1 个移动副；前减振器两端为2 个旋转副；后减振器杆与筒之间为1 个移动副；后减振器两端为2个旋转副；导向摆臂端部为2个旋转副。因此，振动模型中共有8 个低副。在俯仰平面中，每个构件共可存在3 个自由度，每个低副约束2 个自由度。故驾驶室系统的自由度为：6×3-8×2=2个。此外，模型不计驾驶室悬置与导向机构的质量，不考虑它们的惯性力与力矩。图中，m 为驾驶室等效质量的1/2，Kf和Cf分别为前悬置的刚度和阻尼，Kr和Cr分别为后悬置的刚度和阻尼，qf和qr分别为前、后弹簧-减振器总成的位移激励，qW为摆臂支架的位移激励。

2.2 振动微分方程

如图3（b）所示，设整体坐标系O-xyz 的原点O与驾驶室系统静平衡时摆臂与车架的铰接点W 重合，x 轴水平向前，z 轴垂直向上。在车架激励qr、qW和qf共同作用下，即驾驶室后部车架A"点发生位移qr，驾驶室前部车架B"点发生位移qf且W"点发生位移qW，导致摆臂发生转角θ，驾驶室绕着y 轴旋转了角度φ。驾驶室静平衡时，θ 和φ 均为零。由于该系统具有2 个自由度且θ 和φ 相互独立，故选取θ 和φ为广义坐标。

2.2.1 运动学方程

驾驶室中可靠的点位与运动速度是进行动力学建模的基础和关键，因此，必须建立驾驶室关键点位的运动学方程。根据驾驶室及其悬置系统的结构尺寸，可得驾驶室静平衡时各点在坐标系O-xyz 中的初始坐标为A（xA0，zA0），B（xB0，zB0），C（xC0，zC0），D（xD0，zD0），E（xE0，zE0）及W（xW0，zW0）。在车架激励qr、qW和qf共同作用下，各点坐标可分别表示为

式中l为摆臂两个铰接点W和D间的长度。

根据上述点位坐标的解析表达式，求导可得各点坐标的速度和加速度解析表述式。

2.2.2 动力学方程

下面基于所建运动学方程，利用拉格朗日建模方法，建立考虑摆臂约束的驾驶室俯仰平面动力学方程。

驾驶室系统的拉格朗日方程形式为

式中：T、V 和D 分别为驾驶室系统的动能、势能和耗散能；p1和p2分别为广义坐标θ和φ。

驾驶室系统的动能表示为

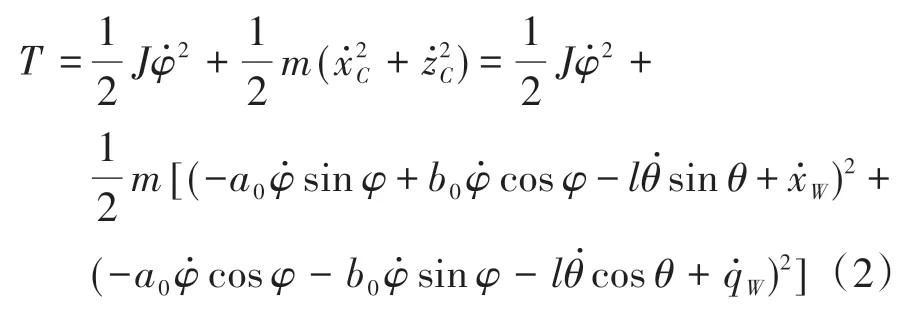
式中：a0= xC0- xD0；b0= zC0- zD0；J为驾驶室绕其质心C的俯仰转动惯量的1/2。

驾驶室系统的势能表示为

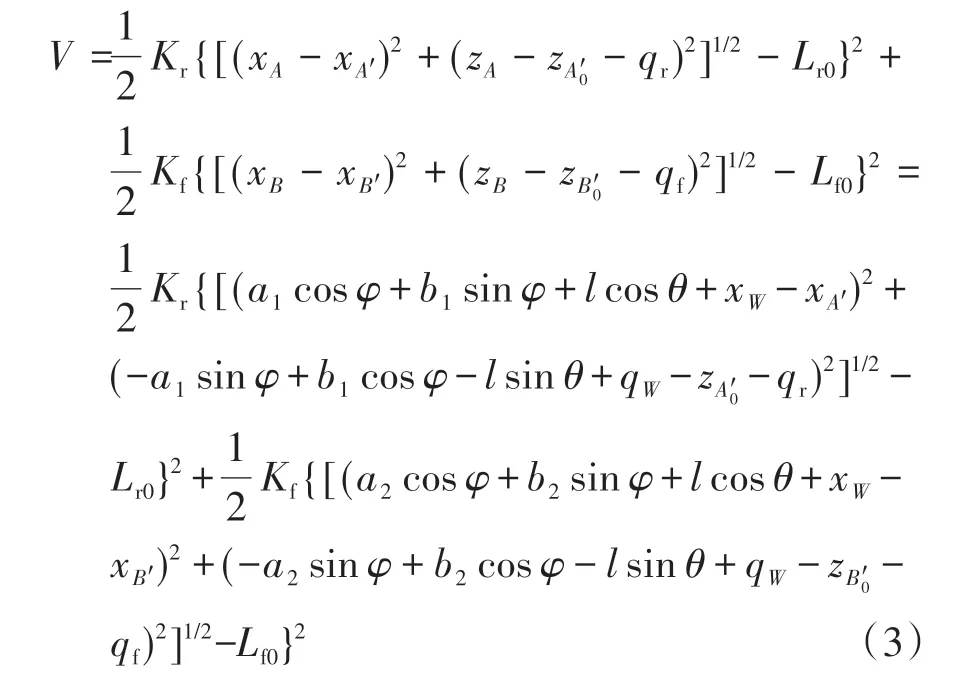
其中：a1= xA0- xD0；b1= zA0- zD0

驾驶室系统的耗散能表示为

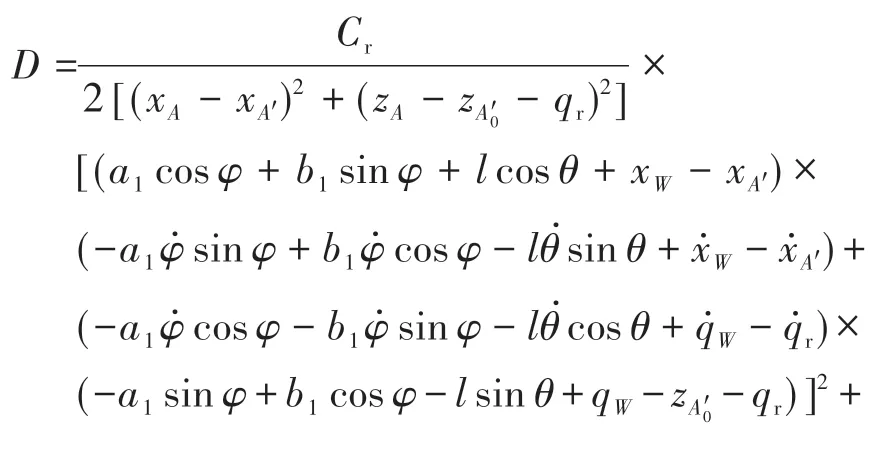
其中：

式中：Cff和Cfy分别为驾驶室前悬置减振器复原行程和压缩行程的阻尼系数［2］；Crf和Cry分别为后悬减振器复原行程和压缩行程的阻尼系数。

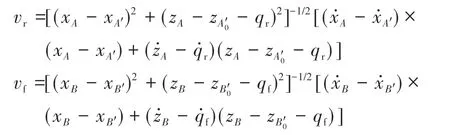
将式（2）～式（4）代入式（1），可得

其中：

将式（2）～式（4）代入F1和F2的表达式，可将式（5）右边进一步表示为关于变量(θ，θ̇，φ，φ̇)的函数，即以θ 和φ 为广义坐标的驾驶室俯仰平面动力学方程为

3 试验验证与模型对比

3.1 整车道路试验与振动信号采集

为验证所建动力学模型的可靠性，以某重型货车为例，参照国标GB/T4970—2009《汽车平顺性试验方法》进行了道路试验，并利用图4（a）所示的LMS Test.Lab 测试设备采集了振动信号。其中，试验车辆驾驶室前、后悬置均采用了螺旋弹簧和双筒式液压减振器。表1 为厂家提供的驾驶室悬置系统参数的试验值。

图4 LMS测试系统和加速度传感器布置

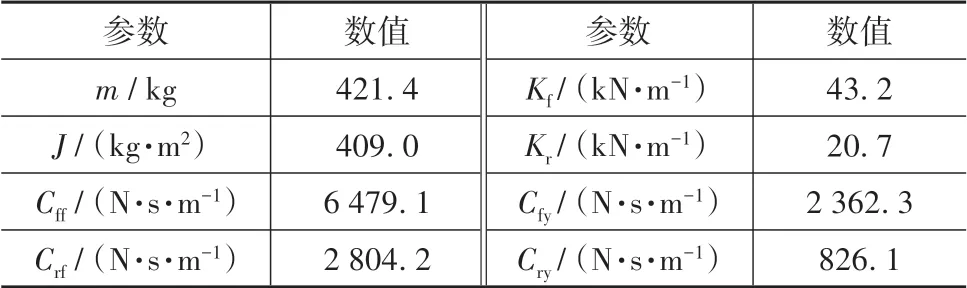
表1 驾驶室悬置系统动力学参数

因本文重点关注驾驶室及其悬置系统，所建模型未考虑座椅悬置系统对驾驶室振动响应的影响，故在试验前拆除了坐垫并将座椅悬置导向机构锁死，使座椅与驾驶室近似刚性连接。试验用加速度传感器的型号为PCB356A26，试验前分别安装在驾驶室地板上和驾驶室前、后悬置安装位置处车架上，如图4（b）～图4（d）所示。其中，因车架上W"和B"点（图3 所示）间距很小，两点激励几乎相同，故在前悬车架仅布置了一个加速度传感器。试验路面为沥青路，分别以50、60、70、80、90 和100 km/h 行驶速度进行道路试验。其中，信号采集时间和频率分别为120 s和400 Hz。6次试验测得的加速度信号时间历程类似。其中，80 km/h 工况下测得的信号如图5所示。

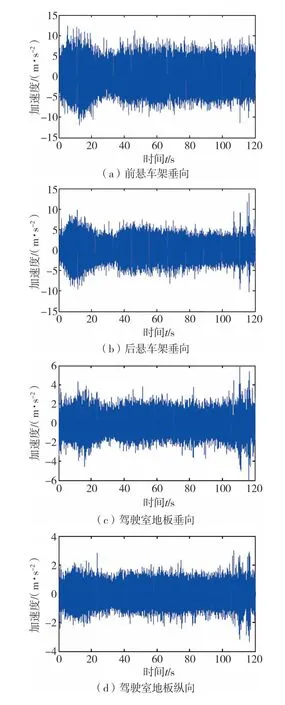
图5 80 km/h工况下测得的加速度信号

3.2 道路试验验证与模型对比

为了进一步验证所建驾驶室俯仰平面动力学模型的可靠性，以前面试验测得驾驶室前、后悬置安装位置处车架加速度信号作为模型输入进行动力学仿真。基于仿真所得驾驶室地板垂向和纵向加速度时间历程，分别算得驾驶室地板垂向和纵向加速度均方根仿真值，仿真值与试验值的对比如表2 所示。表中，不考虑约束情况下的地板纵向加速度仿真值，是首先根据传统不考虑约束的驾驶室俯仰平面动力学模型计算得到俯仰加速度和地板测点与驾驶室质心的垂向距离，然后通过几何换算得到的。

为了进一步考察所建模型与试验的差异，绘制了100 km/h工况下驾驶室地板垂向和纵向加速度响应的时间历程，仿真曲线与试验曲线对比如图6 所示。其中，为了便于直观考察不同曲线的差异，时间轴显示范围设置为0～60 s。

表2 地板加速度均方根仿真值与试验值对比

由表2 可知：基于本文所建考虑约束的驾驶室俯仰平面动力学模型，计算得到的驾驶室地板垂向和纵向加速度均方根仿真值与试验值的最大相对偏差分别为11.3%和14.3%；基于不考虑约束的驾驶室俯仰平面动力学模型，计算得到的垂向和纵向仿真值与试验值的最大相对偏差分别为16.9%和42.2%。与不考虑约束的模型相比，本文所建模型在垂向和纵向的计算精度均有所提高，尽管与试验结果还存有一定的差异。由图6 可知，本文所建模型与试验吻合程度更高，尽管在某些时间点与实际值还存在差异。上述对比结果表明，与不考虑约束的驾驶室俯仰平面动力学模型相比，本文所建考虑约束的驾驶室俯仰平面动力学模型的计算结果更接近工程实际，更能有效复现随机工况下驾驶室系统的真实动力学响应。

图6 100 km/h工况驾驶室地板加速度时间历程对比

造成本文所建模型与试验差异的原因很多，主要原因包括两点：其一，为了避免驾驶室悬置导向机构的弹性连接增加模型自由度，本文所建模型将驾驶室悬置系统导向机构中各部件连接处橡胶衬套的弹性连接简化为运动副连接，因而模型中忽略了橡胶衬套非线性刚度和阻尼特性的影响；其二，所建模型仅局限在驾驶室俯仰平面内，它还不能完全反映其它自由度，具体包括横摆、侧倾和横向等自由度的影响。事实上，驾驶室动力学模型的精度与模型自由度直接相关，模型自由度越多则其精度往往越高，但模型复杂程度也随之提高，给工程应用带来不便。

4 工程应用

传统驾驶室俯仰平面动力学模型仅能用于粗略计算驾驶室垂向和俯仰动力学特性，无法用于计算驾驶室质心的纵向振动特性；本文所建模型考虑了导向摆臂约束的影响，不仅可较准确地计算驾驶室的垂向、俯仰动力学特性，而且可计算其纵向动力学响应特性，同时还可仿真出导向摆臂摆角与减振器前后摆角。本文所建模型不仅具有更高的计算精度，还拓宽了模型的应用范围，因而具有更为广阔的工程应用前景。不仅可用于驾驶室纵向振动响应特性分析、考虑驾驶室纵向振动舒适性的控制策略分析与开发，还可用于导向摆臂摆角估算、减振器前后摆角估算和驾驶室悬置系统动力学参数估计等。下面通过所建模型的工程应用实例，作进一步说明。

4.1 驾驶室质心的纵向振动响应特性分析

据前面分析可知，大多数重型货车的驾驶室，为抑制其俯仰运动，都安装了摆臂导向机构。但由于摆臂的约束作用，驾驶室的俯仰、纵向和垂向运动相互耦合，当车辆受到路面激励时，会导致驾驶室产生纵向振动，进而使得驾驶员产生不舒适感。根据标准ISO2631 可知，在大约3.0 Hz以下，人体对纵向振动比垂直振动更敏感。因此，揭示低频范围内驾驶室质心的纵向振动响应特性对提高驾驶员的舒适性很重要。例如，基于所建模型给出了驾驶室悬置受幅值A=25.0 mm且频率f=1.0，2.0，3.0 Hz的正弦垂向激励时，驾驶室质心的水平位移和加速度曲线，如图7 所示。由图可见，不同频率的垂向激励所引起的驾驶室质心纵向振动差异较大，故在驾驶室舒适性分析时应考虑垂向激励频率对纵向振动响应的影响。

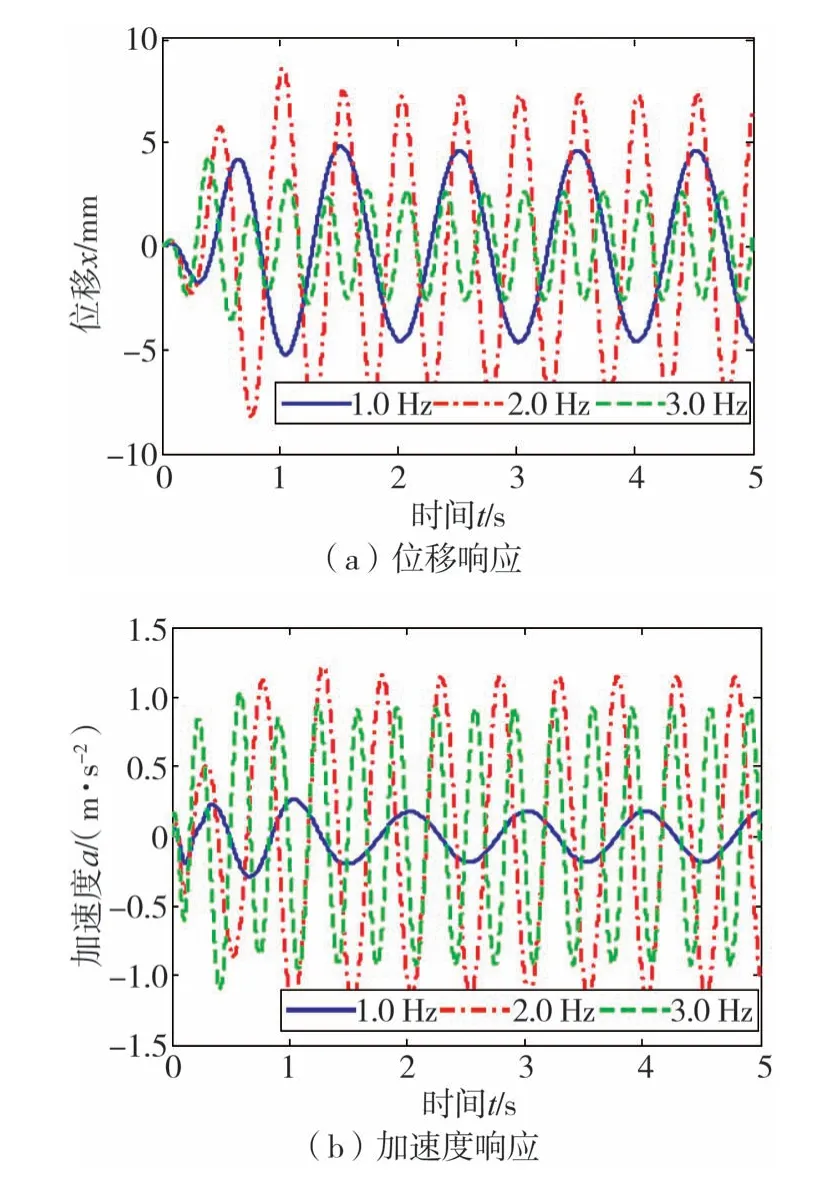
图7 驾驶室质心的纵向动力学响应

4.2 考虑纵向振动的悬置控制策略的分析与开发

驾驶室的纵向振动加速度是驾驶室振动舒适性的重要评价指标［11］。因此，在驾驶室悬置控制策略开发时，通常需要综合考虑驾驶室的垂向和纵向振动。然而，传统模型因无法计算驾驶室质心的纵向振动而不适用于考虑驾驶室纵向振动的悬置控制策略分析与开发。与传统模型相比，本文所建模型提高了计算精度，且在没有增加驾驶室系统自由度的前提下，可以计算驾驶室质心的纵向振动分量，因而适用于考虑驾驶室纵向振动的悬置控制策略分析与开发。

例如，基于本文所建模型，利用最优控制理论［14］，给出了两种最优控制器下驾驶室质心加速度均方根响应，如表3 所示。其中，控制器1 仅以驾驶室垂向加速度最小为控制目标，控制器2 以垂向和纵向加速度的平方和最小为控制目标。表3 表明，与控制器1 相比，在控制器2 情况下，沥青路况下驾驶室质心垂向加速度均方根略有增大，但纵向加速度明显减小，因而进一步提升了驾乘舒适性。可见，在驾驶室悬置控制器开发时，有必要考虑驾驶室纵向振动响应。

表3 沥青路况下驾驶室质心加速度均方根m/s2

4.3 驾驶室悬置导向摆臂的摆角估计

驾驶室前悬导向摆臂的摆动角行程设计，对驾驶室的振动舒适性具有重要影响。在新产品开发初期，常需要提取对标车辆常用行驶路况下摆臂的摆角行程作为摆动角设计域的参考值［11］。例如，表4给出了基于模型得到的上述试验车辆在沥青路上以不同车速行驶时，驾驶室前悬导向摆臂的摆角行程。由表4 可知，随着车速提高，导向摆臂的摆动角行程逐渐增大。表中数据可为同类车型驾驶室悬置导向摆臂摆角的设计提供重要依据和有益参考。

表4 沥青路况下驾驶室前悬导向摆臂的摆角

4.4 驾驶室悬置减振器的摆角估算

减振器摆角的大小，决定着减振器的侧向受力及其端部连接衬套的扭转受力情况，进而影响着减振器总成的使用寿命［19］。因此，在驾驶室减振器总成台架疲劳寿命试验时，常需要提取车辆常用行驶路况下减振器的摆角作为其在台架上安装姿态、摆动范围的参考值［11，19］。例如，表5为基于模型得到的上述试验车辆在沥青路上以不同车速行驶时，驾驶室减振器的摆角情况。由表5 可知，随着行驶车速的提高，驾驶室前、后减振器的摆角行程均随之增大。表中数据可为驾驶室减振器总成疲劳试验设置提供有益参考。

表5 沥青路况下驾驶室悬置减振器摆角

4.5 驾驶室悬置系统动力学参数估计

在驾驶室悬置系统开发时，设计人员常以对标车辆的悬置参数作为参考值［3］。基于传统动力学模型，通过辨识方法可得对标车辆驾驶室悬置系统参数；但因误差较大，很难满足工程要求。其中，辨识结果的误差在一定程度上依赖于所使用模型的计算准确性［17］。此外，尽管设计者可将对标车辆的驾驶室悬置系统进行拆解，利用相应的测试设备对所需求参数逐一测量，但这种方法需要专门测试设备，成本高、测试周期长，甚至因拆解导致悬置损坏而无法测试得到准确的需求参数。为此，下面假设表1 的实际参数值均未知，基于所建模型，利用试验采集数据，通过系统辨识方法进行获取［20］，结果如表6所示。

由表6 可知，基于不考虑约束和考虑约束的驾驶室俯仰平面动力学模型的估计值与实际值的最大相对偏差分别为19.8%和7.9%。可见，基于本文所建考虑约束模型的参数辨识方法，可获得更可靠的驾驶室悬置系统动力学参数值，且该方法克服了直接测量方法的诸多缺陷。此外，对比结果也表明了在建立驾驶室系统俯仰平面动力学模型时考虑导向摆臂约束的必要性。

表6 驾驶室悬置系统动力学参数估计结果

5 结论

针对重型货车驾驶室俯仰平面动力学传统模型计算精度不高且工程应用受局限问题，开展了驾驶室理论建模和试验研究，得到的主要结论如下。

（1）在驾驶室俯仰平面内，由于摆臂的约束作用，驾驶室的俯仰、纵向和垂向运动相互耦合，而非仅发生俯仰运动和垂向运动。

（2）创建了考虑约束的驾驶室俯仰平面动力学模型；基于拉格朗日建模方法，推导了其振动微分方程，并给出了其简洁的解析表达式。

（3）试验结果表明，与不考虑约束的模型相比，本文所建模型的计算结果更接近工程实际，更能有效复现随机工况下驾驶室系统的真实动力学响应。

（4）与不考虑约束的模型相比，本文所建模型计算精度更高，工程应用范围更广，不仅可用于驾驶室纵向振动响应特性分析、考虑驾驶室纵向振动舒适性的悬置控制策略分析与开发，还可用于导向摆臂摆角估算、减振器前后摆角估算和驾驶室悬置系统动力学参数的估计等。