基于分位数回归模型的高水平篮球比赛制胜因素探析
——以2019 FIBA男子篮球世界杯为例
张绍良,董芮,王星,张铭鑫,崔一雄
(1.清华大学 体育部,北京 100084;2.北京体育大学 中国篮球运动学院,北京 100084;3.上海体育学院 体育教育训练学院,上海 200438;4.北京体育大学 体育工程学院,北京 100084)
篮球技战术表现分析是指由技战术分析师或助理教练借助视频分析软件或者比赛追踪系统,观察并标记训练与比赛中团体和个人的技战术行为和事件,通过数据分析和视频反馈等手段,提供给教练员客观和详细的反馈报告,以此帮助教练员了解对手和自己团队的优势与不足,从而改进自己球员的运动表现和优化自己团队的训练计划和比赛策略[1]。目前,技战术表现分析师已经成为国外高水平职业篮球俱乐部中必不可少的重要角色,篮球技战术表现分析相关研究也已经得到了广泛的认可和应用[2]。
当今篮球技战术分析报告主要包括视频与数据分析报告两种形式[3]。在篮球比赛表现分析中,视频分析容易受到教练员的主观认知和经验的影响,从而导致关键技战术特征的选择和对应的分析报告带有明显的个人主观倾向[4]。与之相比,数据分析建模的方式可提供较为客观的反馈信息,纠正教练主观认知的偏差,辅佐其查找比赛过程中遗漏的关键信息[5]。主观与客观的结合可有效地提升教练员团队的工作效率,而数据建模的可视化分析则是当今球队技战术分析中必不可少的环节[5]。
近些年我国篮球比赛数据分析模型大多数采用简单的描述分析、秩和比分析及回归分析,其中一般和广义线性模型是篮球定量分析中被广泛采用的统计模型[6-9]。然而,线性模型描述和解释的仅仅是自变量与因变量条件均值之间的关系,因变量条件均值以外非中心位置的情况是无法用自变量解释的[10]。举例来说,大多数职业篮球联盟或者世界大赛的最终排名与球队的胜率高度相关。当想探寻球队的最终胜率(因变量)与技战术指标(自变量)之间的关系时,教练最主要关注的是处于条件分布低尾的低胜率的球队和分布高尾的高胜率球队等处于因变量非中心位置的情况,而条件均值模型主要考虑的是因变量的均值(即胜率的条件均值与每个自变量的关系),难以扩展到这种非中心位置。因此,篮球比赛分析的研究需要应用更加完善的统计分析方法去解决类似的问题。
本研究以2019年国际篮联(International Basketball Federation,FIBA)男子篮球世界杯32支球队、92场比赛的比赛表现数据为研究样本,运用分位数回归方法探索不同胜率球队的技战术特点。本研究假设高胜率与低胜率球队在技战术应用上存在明显差异,不同胜率的球队强调不同的技战术特点。
1 研究方法
1.1 研究样本和变量
本研究技战术数据来自于FIBA世界篮联官方网站(http://www.fiba.basketball/basketballworldcup/2019/teamstats);高阶数据来自于美国体育数据公司 Synergy Sports Technology (https://www.synergysportstech.com/synergy/)。Zhang等[11]已经对Synergy Sports Technology公司数据的信效度进行了实验验证,该公司所采集的篮球比赛数据与实际比赛中球员的技战术行为存在良好的组间一致性。
根据相关研究的结果,将世界杯中32支参赛球队的最终比赛胜率作为因变量,该变量服从正态分布。其中各参赛队最终胜率(0~100%)所对应的百分位数点(Q10,Q25,Q50,Q75,Q90)呈现在表1中。
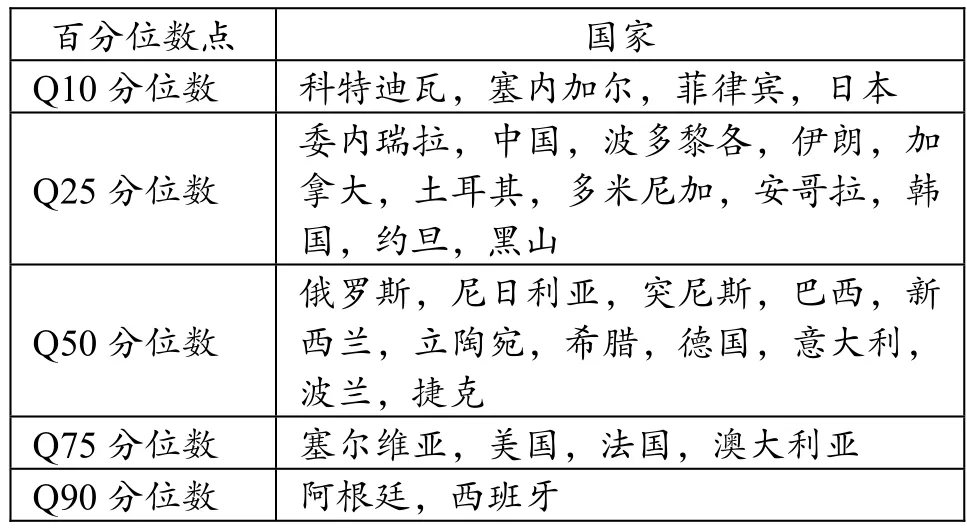
表1 2019年男篮世界杯各参赛球队最终胜率分配
研究所选取自变量包括常规变量、高阶变量和情境变量(见表2)。其中常规变量根据先前的研究基于球权进行了标准化处理[12]。高阶变量是指影响篮球比赛结果的“四因素”,包括有效投篮命中率、进攻篮板球率、失误率和罚球率,这4个指标反映了进攻和防守两个方面对比赛结果的综合影响因素[9]。此外,将对手实力、比赛节奏、比赛的类型作为情境变量,考虑它们对比赛胜率的影响[12]。

表2 自变量及对应分组
1.2 数据统计与处理
1)通过K型聚类分析将对手实力以最终比赛胜率为标准划分为强队(胜率(68±14)%)和弱队(胜率(24±17)%);将比赛节奏根据球队的球权分为快节奏比赛(球权=80.02±3.23)和慢节奏比赛(球权=72.13±2.76);将比赛的类型根据最终比赛分差分为平衡比赛(分差=10.67±6.88)和不平衡比赛(分差=43.21±9.21)[13-14]。
2)使用加权最小二乘法(以下简称 WLS)作为基础模型去探寻常规变量、高阶变量和情境变量与球队胜率之间的关系,有一定的局限性:(1)该方法只能给出因变量条件分布的不完整描述,提供的信息有限;(2)该方法极易受到异常值的影响,不够稳健[10]。本研究同时采取分位数回归(以下简称QR)作为比较模型去解决上述问题。首先,分位数回归能描述和解释自变量对因变量不同位置的影响,从而能提供观测变量之间更全面的信息[15]。其次,该方法使加权误差绝对值之和最小来估计回归参数,所以回归系数更加稳健,对异常值的敏感程度也远远小于加权最小二乘回归[16]。再次,分位数回归模型对随机误差项的分布没有假设,当误差项不服从正态分布时,分位数回归比加权最小二乘法回归更有效[15]。最后,在回归系数的解释方面,加权最小二乘回归解释的是自变量对因变量平均值影响,而分位数回归描述的是自变量对因变量特定分位数水平上影响的边际效果,即分位数回归可以提供不同分位点处的估计结果[10]。
上述所有的统计分析和数据可视化通过 R软件(version 3.2.2,Vienna, Austria) 完成,其中分位数回归模型建构使用的是‘quantreg’包中的“Ker”函数,两个模型中,Alpha值均被设定为0.05[12]。
2 结果与分析
WLS和QR回归系数的描述和对比呈现在表3中,显著性变量总结呈现在图1中。
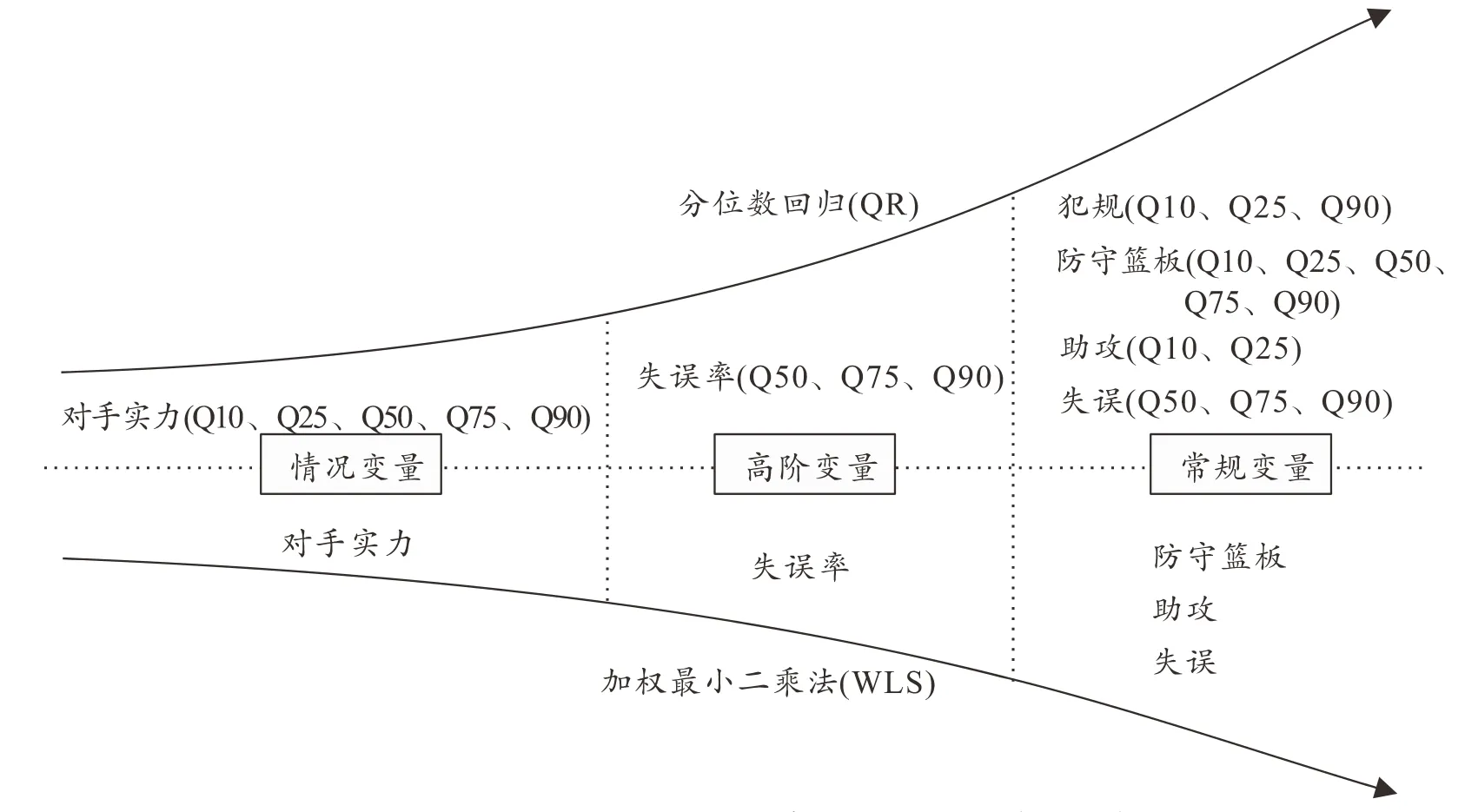
图1 WLS回归和QR回归区分比赛结果的显著性变量示意图
在Q10分位点上对应的是胜率最低的球队,有科特迪瓦、塞内加尔、菲律宾、日本,这些球队的胜率处于该条件分布的10分位数处。从QR回归结果中可以看出,对手实力(ß=-0.126,P<0.01)对于比赛胜率有显著的负向影响,但是防守篮板(ß=0.015,P<0.01)、助攻(ß=0.010,P<0.05)、犯规(ß=0.009,P<0.05)这 3 项指标对于比赛胜率有显著的正向影响。
在Q25分位点上对应的是胜率较低的球队,代表球队有委内瑞拉、中国、波多黎各等,这些球队的胜率处于该条件分布的25分位数处。从QR回归结果中可以看出,对手实力(ß=-0.181,P<0.01)与比赛胜率有显著的负相关性,但是防守篮板(ß=0.013,P<0.01)、助攻(ß=0.006,P<0.05)对于比赛胜率有显著的正相关性。
在Q50分位点上代表了本届世界杯的平均水平,代表球队有俄罗斯、尼日利亚、突尼斯等。从QR回归结果中可以看出,对手实力(ß=-0.198,P<0.01)、失误(ß=-0.169,P<0.01)、失误率(ß=-18.02,P<0.01)对于比赛胜率有显著的负向影响,但是防守篮板(ß=0.010,P<0.01)对于比赛胜率有显著的正向影响。
在Q75分位点上对应的是胜率较高的球队,有塞尔维亚、美国、法国、澳大利亚,这些球队的胜率处于该条件分布的75分位数处。从QR回归结果中可以看出,对手实力(ß=-0.171,P<0.01)、失误(ß=-0.133,P<0.05)、失误率(ß=-13.62,P<0.05)与比赛胜率有负相关性,但是防守篮板(ß=0.007,P<0.05)与比赛胜率有正相关性。
在Q90分位点上对应的是胜率最高的球队,有阿根廷和西班牙,这些球队的胜率处于该条件分布的90分位数处。从 QR回归结果中可以看出,对手实力(ß=-0.219,P<0.01)、犯规(ß=-0.004,P<0.05)、失误(ß=-0.137,P<0.05)、失误率(ß=-13.66,P<0.05)对于比赛胜率有显著的负向影响,但是防守篮板(ß=0.011,P<0.05)的增加会导致胜率的增加。
值得注意的是,当将WLS和QR回归模型进行比较时发现,在WLS回归中犯规这项指标与比赛胜率的关系并无统计学意义,但是在QR回归中发现,对于低胜率(Q10)和(Q25)球队来说,增加犯规将会导致胜率的增加,然而对于高胜率(Q90)球队来说,增加犯规将会导致胜率的减少。
3 讨论
本研究结果证实了最初的假设,在本届世界杯中,高胜率球队与低胜率球队在技战术应用上存在着相似和异同点。对于低胜率球队,助攻和犯规的增加可以提高比赛获胜的概率;对于高胜率球队,减少犯规和失误会导致胜率的提高;对于所有的球队,防守篮板是关键的制胜指标,增加防守篮板会增加获胜的概率。值得注意的是,对手实力对于比赛的结果有重要影响,这更加考验球员在比赛过程中的应变能力和教练员技战术的使用策略。此外,通过对比WLS和QR回归模型发现,QR回归结果进一步补充说明了WLS多元回归的结果,并对各项技战术指标对不同胜率的球队所造成的影响给出了更详尽的解释。因此,从本研究结果可以看出,分位数回归模型在篮球比赛表现分析的研究中具备较好的模型稳定性与结果可解释性,可以帮助教练员实现更加有效的比赛总结和对手分析,从而进一步优化训练和比赛策略。
从研究结果发现,对手实力这一情境变量和球队的胜率存在着明显的负相关关系,相比较对阵弱队,各参赛队在对阵强队时,胜率会明显降低。这种现象从低胜率球队贯穿到高胜率球队,这与 Anthony等[17]对于奥运会和世界篮球锦标赛的研究结果是一致的。该研究认为奥运会和世界篮球锦标赛与各个国家职业篮球联赛的最大区别在于,球队整体实力之间的差距呈现两极分化,欧洲和美洲球队的整体实力明显高于亚洲和非洲的球队。因此在世界杯等国际大赛中,实力较强的对手给教练员和球员在心理、体能和技战术上带来不同程度的压力,从而影响球队比赛的结果,这种现象对于亚洲和非洲球队的影响更加明显。
在本研究中,防守篮板与比赛获胜的概率呈现显著的正相关。防守篮板已经被证明是高水平篮球赛事中的关键制胜因素[13,17-21],Sampaio等[21]研究表明,教练员在国际大赛备战过程中,要发展或者选择具备侵略性防守意识的上线球员;防守后卫应在上线给予对位的进攻后卫强大的压力,迫使他们造成失误和被迫投篮;前锋和中锋需加强卡位意识,确保篮板球的成功率。同时后卫与中锋和前锋的有效交流是确保防守篮板球成功率和迅速发动快攻的关键。因此在国际大赛的备战过程中,教练员需要从数据背后的关键细节出发,提升球员能力和球队表现。
虽然 WLS回归显示助攻的增加导致比赛胜率的提高,但是结合QR回归发现,这种现象仅仅对低胜率(Q10和Q25)的球队有显著性意义。这个研究结果与Zhang等[12]的研究结果是一致的:助攻是球队整体有效配合的一个重要测试指标,这项指标不仅体现了帮助队友得分事件的频数统计,同时也反映了最后成功投篮前无球和有球队员之间固定战术配合的完成程度。上述发现也被Karol等[22]研究证实,强队与弱队在世界大赛中最主要的区别就是篮球技战术整体配合熟练程度的差异。强队在边线球、底线球、半场配合、攻防转换、暂停后、比赛最后时刻所执行的战术成功率要明显高于低胜率和实力较弱的球队,同时在执行上述战术固定配合的数量和质量上也远远高于后者。此外,WLS回归显示,失误和失误率的减少将会导致比赛获胜概率的提高,但是QR回归给出了更详尽的解释,这两项指标对中等胜率(Q50)和高胜率(Q75和 Q90)的球队有显著性意义。该发现也与 Anthony等[17]的研究结果一致:在世界杯比赛中,强队在体能和技战术上虽然占有优势,但是,如果在比赛中某阶段频繁的失误会给球员带来心理层面的压力,如果单节失误过于频繁,教练员应该及时选择换人和轮转新的阵容以确保既定战术的有效实施和重振球员信心。
值得注意的是,在WLS回归结果显示个人犯规与比赛胜率不存在相关关系,但是QR回归发现,对于本届世界杯中低胜率(Q10)球队来说,增加犯规会提高比赛的胜率,而对于高胜率(Q90)球队来说,却会导致其比赛胜率的降低。Miguel等[24]研究也证实了这一点:在国际大赛中,低胜率球队的教练可以更多地使用犯规战术,打破进攻球队原有的技战术配合和比赛节奏,让进攻球队通过罚球的方式完成进攻。但高胜率球队则要减少犯规,以保证先发球员的进攻优势可以延续到比赛的最后阶段和关键时刻。本研究结果一方面给低胜率和高胜率球队提出了不同的比赛策略,另一方面也论证了在篮球比赛数据分析中,分位数回归相比传统回归模型的优越性和实际应用价值。
这项研究可能是第一个将分位数回归模型应用在篮球比赛分析领域的,存在一些局限性。首先,研究的样本仅使用了 2019年男篮世界杯各参赛球队的比赛表现数据,推荐未来的研究扩充样本量或者从纵向研究的角度去探索比赛结果与比赛表现指标之间的关系。其次,研究考察了情境变量对技战术行为的独立影响,推荐未来的研究可以考察情境变量对技战术行为的交互影响。最后,虽然新的数学模型扩展了传统线性回归模型的结果,但是篮球运动的本质是非线性的,未来研究可以考虑使用马尔可夫链和卷积神经网络等机器学习的方法,探索在比赛动态时间变化中,各项技战术指标对于最终比赛结果的影响,以此提供给教练团队更加详细的赛事总结报告。
4 结论
通过WLS回归和QR回归模型对2019年男篮世界杯比赛数据的分析可以得出:对于所有球队,防守篮板是关键的制胜指标。相比较对阵弱队,各参赛队在对阵强队时,胜率会明显降低,增加防守篮板可以显著增加比赛获胜的概率。对于低胜率球队,助攻和犯规与比赛的最终胜率存在正相关性,增强球队的有效进攻配合以及合理的使用犯规改变进攻球队的比赛节奏和既定战术可能是取得最终胜利的关键。对于高胜率球队,犯规和失误与比赛的胜率存在负相关性。因此,在进攻和防守中,减少不必要的犯规和传运球等配合的失误有利于最终比赛的胜利。

