改进的BP算法在多声道超声波流量计中的应用

郑安芳，杨 帆，2

（1.武汉工程大学 电气信息学院，武汉430205；2.湖北省视频图像与高清投影工程技术研究中心，武汉430205）

多声道超声流量计在大型水电站、泵站和输水供水工程中得到广泛应用，根据应用对象的不同分为两类，一类应用于理想流场分布的流体，其研究内容已经比较成熟；另一类应用于非理想流场分布的流体，众多学者为了提高流量计在该条件下的精度和准确度，提出了多种多声道超声流量计的流量计算算法。文献[1]提出了一种用实际流速分布代替理想流速分布， 解决Gauss-Jacobi 积分方法中流速固定的问题，但是当声道数过少时将会影响权重计算的准确度。文献[2]提出了一种利用非线性最小二乘法计算各声道权重的方法，根据最小误差均方值选取权重系数，该算法适用于声道高度无法改变的结构中。文献[3]提出了利用Gauss-Legendre 数值积分方法求解流速非均匀分布的四声道气体超声流量计的位置和权重系数，但用多项式法表达非均匀分布的流速误差较大。文献[4]提出了基于Kalman滤波的多声道流量融合方法，该算法测量的范围存在极限。

针对非理想流场情况下多声道流量融合存在的误差大、声道高度固定等问题，本文提出了一种基于改进的BP 算法的流量计算方法，该方法声路高度可以改变，其次其测量精度更高、测量范围更广。

1 多声道明渠流量计流量计算原理

时差法超声波明渠流量计根据超声波在液体中顺流方向和逆流方向的传播时间差来计算流体的速度和流量，原理如图1 所示。

图1 利用超声波测液体流速原理Fig.1 Principle of measuring liquid velocity by ultrasonic wave

令超声波通过换能器时的顺流时间为t1，逆流时间为t2，则流速v 的取值为

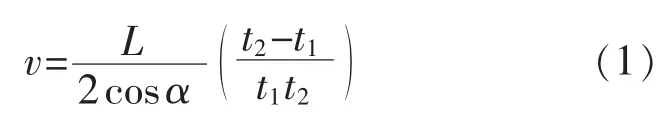
式中：L 是声路长度；α 是声路与水平流速的夹角。

单声道超声波流量计已经不能满足人们的日常需要，多声道超声流量计凭借其测量结果的准确性，在实际生产生活中被广泛应用，其测量原理如图2 所示，hi表示第i 条声路的高度。多对换能器将被测量管道划分为几个区域，若将几对换能器平行对称放置，则可知道第i 声道的速度为

式中：t1i、t2i分别表示第i 条声路的逆流和顺流时间；vi表示第i 条声路的速度。

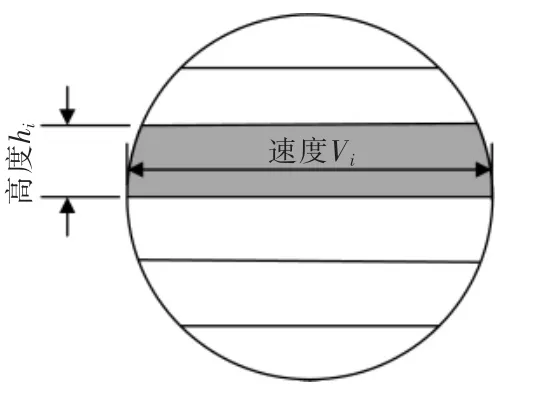
图2 多声道超声流量计测量原理图Fig.2 Measurement principle diagram of multi-channel ultrasonic flowmeter

由定积分计算原理可知， 若管道半径为R，hi=tR 且取值很小，t 为相对管道高度，则多声道明渠流量计的流量计算方法为

研究发现多声道明渠流量计的声道数过多时对于提高精确度的贡献不大， 且增加计算难度，一般3～6 个声道数就能满足实际需要，本文选取声道数为4 进行研究，由高斯积分公式可知流量为

因此，式（3）可以等效为

式中：Ak为高斯系数；tk为高斯点。

根据Gauss-Jacobi[5]求积公式，得到声道位置权重系数为

式中：n 为声道数。由式（6）可知，当n 确定时，Gauss-Jacobi 积分公式得到的权重值是固定的， 此种计算流量的方法适用于理想状态下的流体。但是在实际情况中，因为流体不纯净，管道中存在阻流件等情况的存在，使得明渠流量计测量的液体流速在管道内部非对称分布，因此需要根据实际情况优化流量计算方法，提高流量计的精度。

2 基于改进的BP 算法的流量计算

BP 神经网络算法[6-7]，具备很强的自学习和自适应能力，且容错性好[8]，是一种优秀的数据融合算法。该算法模型的核心思想是根据实际输出信号和期望输出信号之间的误差值，来调整和修订各节点的权值来满足实际需要。在已有的适用于非理想流动的流量算法的基础上， 提出一种基于BP 算法的流量计算方法。

2.1 BP 算法结构设计

（1）网络初始化。设置BP 神经网络的输入层信号为4 个声道的流速值v1，v2，v3，v4，隐藏层节点数2个，输出层节点数1 个，相邻节点间的权值设置如图3 所示。

图3 BP 算法结构图Fig.3 Structure of BP algorithm

（2）计算隐藏层输出hj。

（3）计算输出层输出yj。

（4）根据误差变化量Δwi和学习率mi，更新权值wi。

（5）设定学习次数。当学习次数完成并且实际输出yj与期望d 的均方误差满足条件， 则结束训练，否则返回步骤（2）。

2.2 BP 算法的改进

常用的BP 算法网络采用单一的激活函数或不同层之间应用不同的激活函数，经典激活函数包括S 型函数， 双曲正切函数等， 由于其输出映射范围小，会对输出的实际值进行压缩，将不适用于流量的计算；ReLU（Rectified Linear Unit，线性整流函数）函数及其改进的多种修复线性函数可以加快网络的收敛速度，但是对学习率十分敏感，容易出现神经死亡。因此根据实际需要，提出一种在一个神经网络中同层间采用多激活函数的BP 算法。当一种激活函数出现神经死亡时，另一种激活函数可以进行替补。在图3 所示的BP 算法结构图中，令隐藏层节点1 所在支路选用激活函数f（x），隐藏层节点2所在支路选用激活函数g（x），隐藏层和输出层之间的激活函数为h（x）。

误差函数选择均方误差函数pp，将期望值z 与实际值输出值y 作比较：

学习率mi会根据权值wi的偏导数dwi的变化而变化

3 仿真验证与结果分析

计算流体力学[9]（computational fluid dynamics，CFD）是通过计算机分析流体流动情况的一种技术[10]，在流体输送过程中，依据地势和实际空间结构，需要选择不同形状的管道，流体力学研究表明弯管内的流体在流动过程中流场呈现非理想流动状态，这一现象的存在将会影响流量计的精度。本文通过ANSYS 19.0 软件，对经典的90°单弯管和异面双曲管进行流场模拟。应用ANSYS 19.0 软件在Workbench界面内建立工程文件，在Geometry 界面建立几何模型，并对模型进行填充，在Mesh 界面进行网格划分，定义进出口面，在Fluent 界面对典型的上游单弯管和上游异面双曲管管道模型进行仿真模拟，在模型中管道内径D=100 mm。通用设置设定管道内的液体为water-liquid，入口水流速度inlet 依次设定为1 m/s，2 m/s，4 m/s，…，20 m/s，湍流模型选择RNG，算法选择SIMPLE，收敛残差为e-6，声道角度与水平面夹角为45°。

3.1 90°单弯管仿真

90°弯管的结构图如图4 所示， 当输入流速为10 m/s 时， 得到弯管下游5D 和10D 处的速度云图如图5、图6 所示。由图可知，在下游5D 处由于弯管产生的二次流影响使流速呈现明显的非对称分布，此时4 声道超声波流量计的安装角度和相对声道高度将会对流量计算的准确性产生较大的影响，在下游10D 处由于水流经过一段时间的直管流动，流速已经趋于比较对称的状态，这也是工程上选择将流量计一般安装在下游10D 处的原因。在文献[2]和文献[5]中，分别利用李雪松的非线性最小二乘法和Gauss-Jacobi 法进行流量计算，计算结果误差小。选取文献[5]中的声路高度，在仿真结果中依次读取1 m/s，2 m/s，4 m/s，…，20 m/s 处四个声道的流速值，并选择如表1 所示的权重系数计算得到实际的流速值， 将其结果和改进后的BP 算法流量计算结果进行对比， 其误差均方值对比曲线如图7、 图8 所示，由图可知，在相同声路高度下，三种流量计算方法取得的均方误差值都小于0.03%， 流量计算精度较高，但是相比之下本文流量计算方法下的误差最小，当流速在16 m/s 左右时，误差小于e-6。

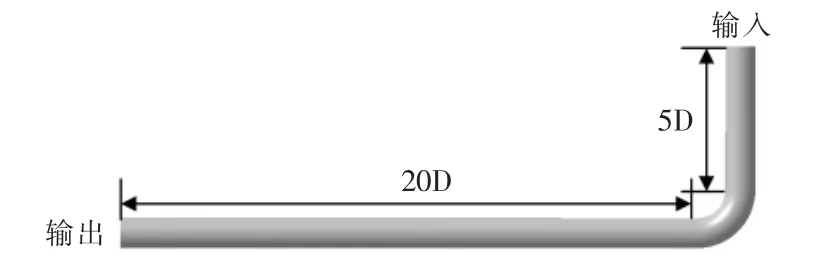
图4 90°单弯管结构图Fig.4 Structure of 90° single elbow

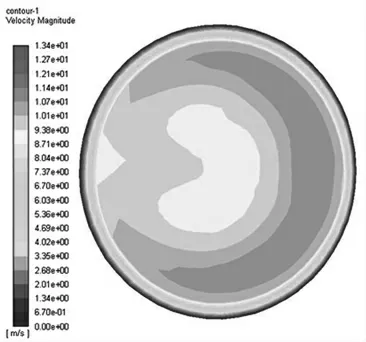
图5 90°单弯管下游5D 处速度云图Fig.5 Velocity nephogram at 5D downstream of 90°single elbow

图6 90°单弯管下游10D 处速度云图Fig.6 Velocity nephogram at 10D downstream of 90° single elbow

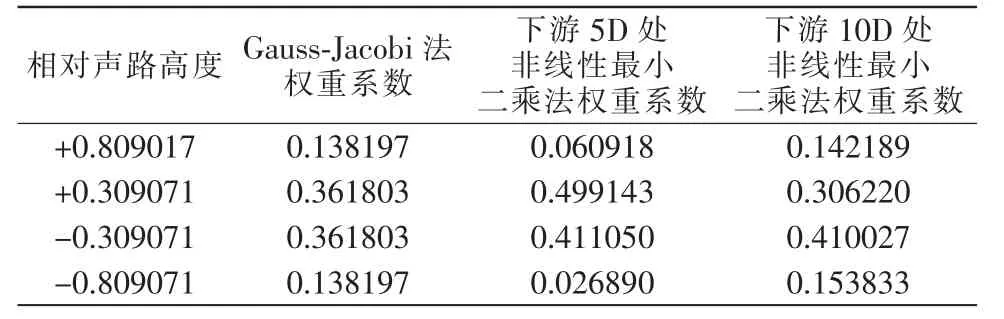
表1 90°单弯管下游5D 处和10D 处声路高速和权重系数表Tab.1 Sound path velocity and weight coefficient at 5D and 10D downstream of 90°single elbow

图7 90°单弯管下游5D 处流速均方误差曲线Fig.7 Velocity mean square error curve at 5D downstream of 90°single elbow

图8 90°单弯管下游10D 处流速均方误差曲线Fig.8 Mean square error curve of velocity at 10D downstream of 90°single elbow

3.2 异面双弯管仿真

异面双弯管结构图如图9 所示，当输入流速为10 m/s 时，得到弯管下游5D 和10D 处的速度云图如图10、图11 所示。异面双弯管在工业现场广泛应用，由两个单弯管组合构成，在实际流场中存在涡流和二次环流现象，其非均匀分布的流场对测结果的准确性影响很大。在ANSYS 中测得异面双曲管在下游5D 处和10D 处的流速值，由文献[2]和文献[5]可知，各声道流速值与表2 对应的各声道权重值加权求和即可得到流量计测得的流速值，将Gauss-Jacobi 法、李雪松的非线性最小二乘法与改进的BP算法得到的流速值分别与期望值进行作差，得到相应的误差函数曲线如图12、图13 所示，由图可知，在5D 处文献[2]和文献[5]的误差十分接近，在10D处文献[2]的误差与文献[5]的误差随着流速的增大而增大，本文BP 算法的均方误差值一直都很小，小于0.05%，明显优于文献[2]和文献[5]中的算法。

图9 异面双弯管结构图Fig.9 Structural diagram of double elbow with different faces

图10 异面双弯管下游5D 速度云图Fig.10 5D velocity nephogram downstream of double curved pipe with different faces

图11 异面双弯管下游10D 速度云图Fig.11 5D velocity nephogram downstream of double curved pipe with different faces

表2 异面双弯管下游5D 处和10D 处声路高速和权重系数表Tab.2 Sound path velocity and weight coefficient at 5D and 10D downstream of opposite face double elbow

图12 异面双弯管下游5D 处流速均方误差曲线Fig.12 Mean square error curve of velocity at 5D downstream of double bend

图13 异面双弯管下游10D 处流速均方误差曲线Fig.13 Mean square error curve of velocity at 10D downstream of double bend

3.3 不同声路高度误差对比

各种数值积分法在测量理想分布流场时对声路高度的固定值都有十分明确的要求，在测量非理想流体时众多学者依然采用数值积分法算得的声路高度， 主要研究的重心偏向权重取值方面的探索。本文研究了不同声道高度对流速的误差影响情况，将固定声道高度（表1、表2）下测得的流速值与将声道等距分布的流速值分别求得均方误差，其结果如表3 所示，两种声路高度的误差值均明显小于0.03%，结果表明该算法适用于不同的声路高度，在实际施工现场给流量计安装带来较大的便利。

4 结语

利用ANSYS 软件对90°单弯管和异面双曲管建模， 将取得的流速值依次代入Gauss-Jacobi 流速计算法，非线性最小二乘法流速计算法和改进的BP算法中，结果表明，非线性最小二乘法流速计算法的误差最大，Gauss-Jacobi 流速计算法的误差次之，改进的BP 算法误差最小，且改进的BP 算法可以适用于不同的声路高度下的流量计算。改进的BP 算法不仅克服了在非理想流场下流速分布不均造成流量测量误差较大的缺点，而且提高了流量计在测量非理想流动时的精度，其声路高度可调，给流量计的实际安装增加了便利。

表3 两种声路高度流速均方误差值对比表Tab.3 Comparison of mean square error of velocity at two sound path heights