多变量灰色模型的优化及其应用

（临海市水利投资开发有限公司，浙江 台州 317000）

0 前言

沉降监测目前在软土地基、高边坡、深基坑等施工中被广泛采用，但因施工工艺、工期等复杂因素的影响，使得实际的沉降监测只能反映当前工况下的短期规律。为合理缩短工期、节约工程建设成本，利用实测沉降数据，通过建立数学模型，分析预测沉降系统未来发展的总体趋势及稳定标准，为施工、设计提供控制参考，已成为一种常用方法。当前，沉降预测主要有有经验公式法、灰色系统法、遗传算法等，每一种方法都有其自身的特点和适用性。

灰色系统由邓聚龙提出，“贫信息”“小样本”是其重要的特点。目前利用灰色模型预测沉降主要集中在GM(1，1)模型、多变量 MGM(1，n)模型及其改进模型，未考虑相邻测点间存在的变形协调、影响制约关系。本文通过分析灰色模型初始灰微分方程和白化微分方程的建模特点，以背景值和灰导数同步优化为基础，建立了与系统变形协调相适应的新NMGM(1，n)模型。结合工程实例，表明优化的模型在具备良好的原始数据拟合精度的基础上，同时具有良好的预测效果。

1 多变量模型的关联度

需要注意的是，利用多变量灰色模型预测沉降前，需对原始数据序列进行相关性分析，以确定数据序列的关联度，校验测点间变形协调是否具有相关性，具体方法可参见文献，一般认为当各测点间的关联度大于0.5时，具有较高的关联度，即可利用多变量灰色建模预测沉降。

2 NMGM（1，n)模型建模

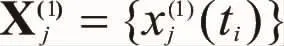
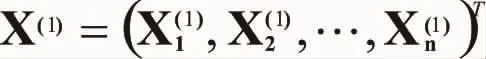
在n个测点满足关联性的前提下，建立NMGM（1，n）模型一阶白化微分方程组：

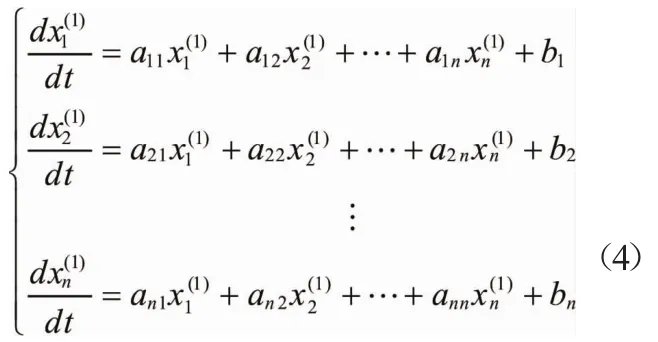
令参数矩阵

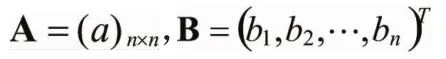
变量矩阵

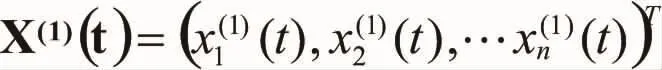
则式（4）变换形式为：

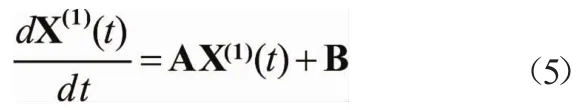
式（4）离散化可得模型的灰微分方程为：

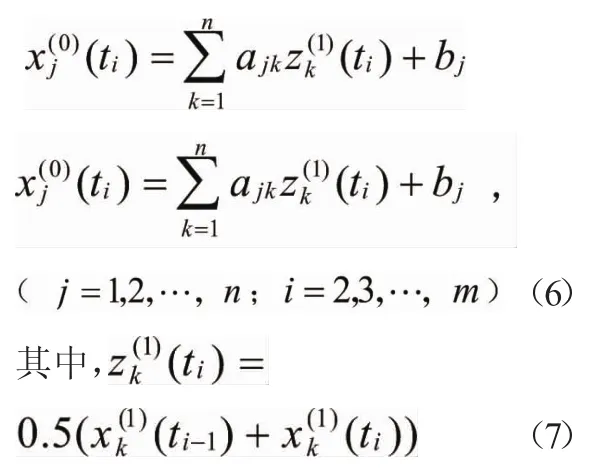
式（7）即为模型背景值，即紧邻均值生成序列

辨识参数A、B可根据二乘法原理估算：

式中，

由此，得式（5）离散化的时间响应式为：

由式（12）累减还原得原始数据预测值：

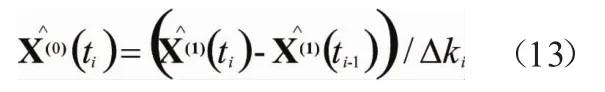
3 NMGM（1，n）模型的优化

3.1 灰导数和背景值的优化

根据式（4）及t点的导数定义有：

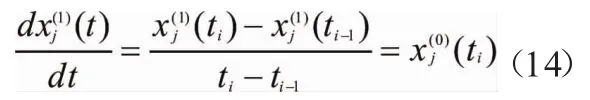
则式（4）差分离散化后的灰微分方程为：

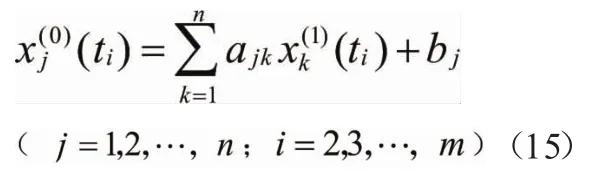
式（4）与式（15）存在替代系统误差。为减少这一误差，本文对模型进行如下优化。

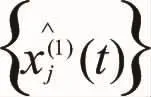
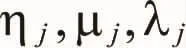
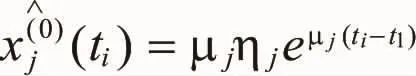
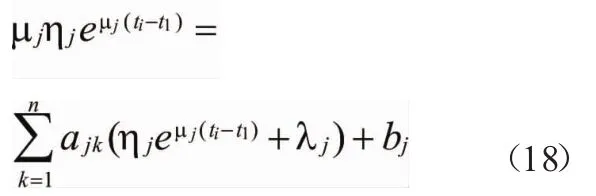
待定参数可求解如下：

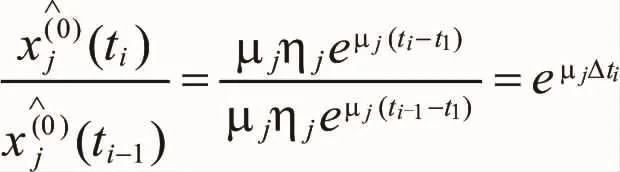
可知，

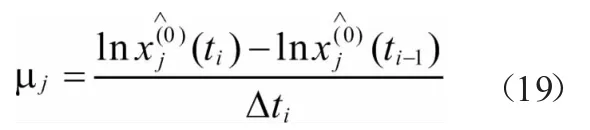
即

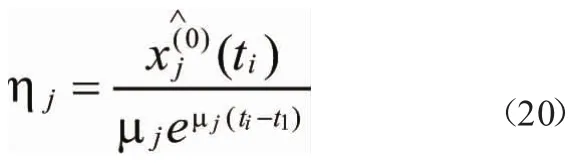
根据初始条件（i=1），

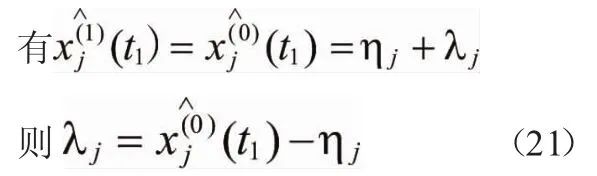
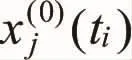
为此，以残差的平方和分别构造指标函数：

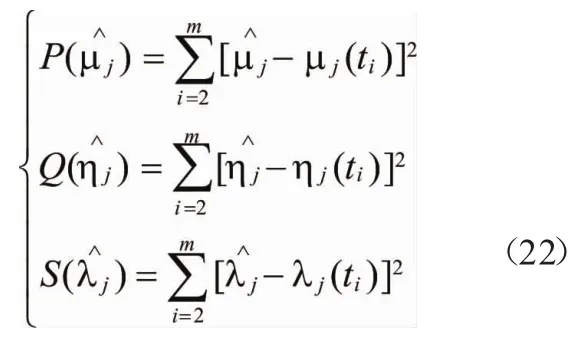
3.2 初始条件优化

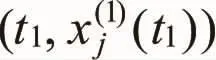
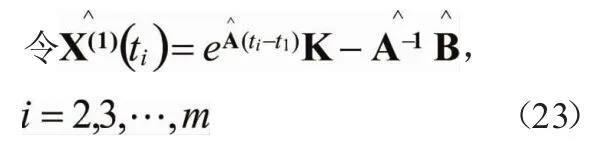
K的求取方法如下：

由序列累加生成可知

3.3 模型精度检验

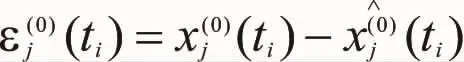
每期预测值与实测值相对误差：

平均相对误差：

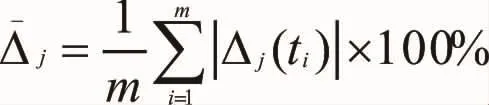
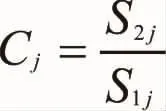
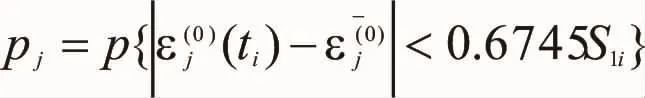
3.4 优化NMGM（1，n）模型计算步骤

根据上述原理，具体计算步骤如下：

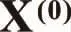
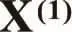
③计算优化的灰微分方程模型式（18）；

④根据新模型按式（8）求取参数A、B；

⑤按式（23）优化初始条件；

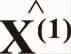
4 工程实例

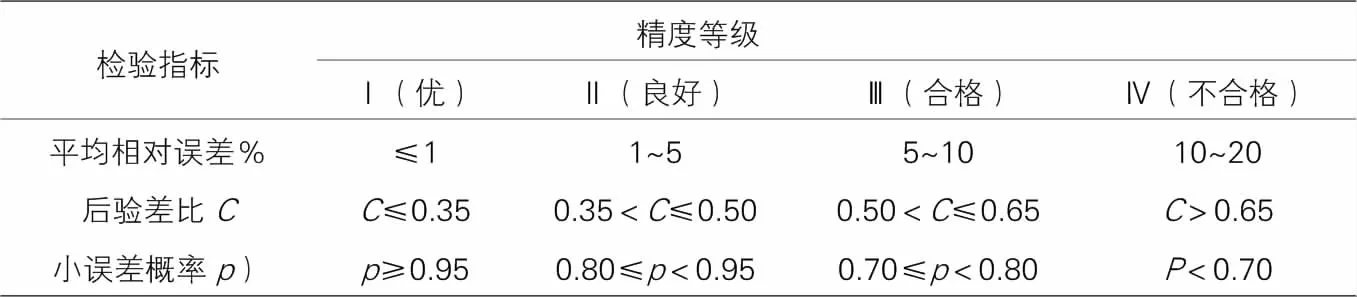
精度检验参考 表1

监测点拟合及预测结果 表2

4.1 原始监测数据

某项目路基横断面左（A）、中（B）、右（C）共埋设三个沉降测点，堆载预压7.23m，设计预压期10个月，选取12期原始监测数据序列。原始数据序列如表2中所示。

4.2 NMGM（1，3)模型优化计算

根据灰色关联分析方法，计算三个测点原始数据序列的灰色关联度均大于0.5，可见各点间沉降存在关联性，可以利用NMGM(1，3)模型建模预测。通过编制计算程序，由实测数据求得三个测点的拟合值及预测值如表3。

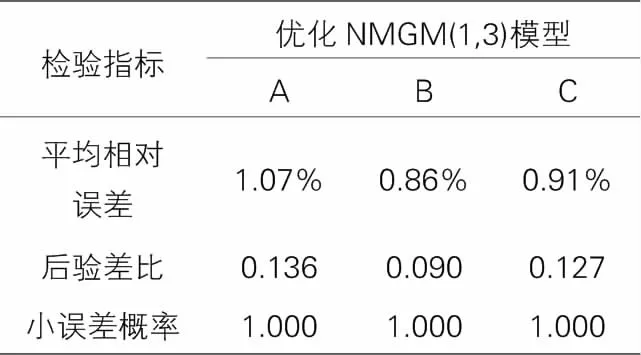
拟合值精度检验 表3

4.3 沉降拟合及预测分析

根据表2中前8期NMGM(1，3)模型拟合值精度结果可见，三个测点每期数据拟合的相对误差均小于2%，对每个测点的拟合误差相对平均，无异常点，说明优化后的模型具备较高的实测数据拟合精度。表4中进一步表明，三个测点的平均相对误差仅为1%左右，后验差比指标亦达到了Ⅰ级的优良等级；小误差概率指标上，每个测点的的拟合精度保证了100%。拟合效果的检验说明优化后模型具备良好拟合精度，对后续用于沉降预测是可行、有保证的。

分析表2中后4期的实测数据预测计算结果表明，优化的NMGM(1，3)模型在对第9至11期预测的相对误差均较小，最大误差仅为B点第11期的7.62%，可以满足工程预测精度要求。受预测周期的影响，对第12期的预测相对误差增大，最大为15.38%，均未超过20%，基本可以接受。其中，三个测点对后4期预测的相对误差平均值分别最大为6.54%（测点B），其余均未超5%。需要注意的是，实际上，本文1～8期的累计沉降观测时间为51天，而后4期的沉降预测周期共计88天，这也充分体现出灰色系统“小样本”“贫信息”的预测特点，在短期预测精度和效果上，完全能够满足工程实际应用需求，预测精度比较理想。

综合上述计算及分析，通过基于灰导数优化的同步背景值优化方法建立的优化的NMGM(1，n)模型，实际上是对原始序列及累加后的序列进行了一次平滑拟合，使得实测散点数据序列更加符合指数函数的特征，降低了异常数据变化值或人为误差的影响。优化后的NMGM(1，n)能够较好地体现各沉降监测点间系统关联性，符合沉降监测系统的变形协调实际工况，能够比较真实地反映出沉降监测系统变形发展的总体趋势，具有良好的拟合预测效果。

5 结论

①本文通过灰导数和背景值同步优化的方法，从初始形式灰微分方程出发，建立了优化的NMGM(1，n)模型。

②通过工程实例说明，所建立的优化的NMGM(1，n)模型能够较好地体现各沉降监测点间系统关联性，具有良好的拟合预测效果，能够满足工程实际应用需求。