基于Landsat-8 OLI数据的马尾松林蓄积量饱和点确定及估测
孙忠秋,吴发云,胡 杨,高显连,高金萍
(1.国家林业和草原局调查规划设计院,北京 100714;2.宁夏大学,银川 750021)
基于遥感数据进行森林参数提取是林业领域中进行森林资源监测的一项重要手段,通过遥感数据的光谱信息,联合地面样地调查点的数据进行建模与反演,便可获得一定精度范围内的森林资源估测结果。目前基于遥感数据进行森林资源估测的研究有很多,如毛学刚等[1]使用Landsat长时间序列数据估测了我国东北部分区域的树高,结果表明使用长时间序列的数据比单时相数据估测效果好,RMSE降低了0.50 m而模型估测精度提高了6.34%;周小成等[2]基于两期高分辨率无人机影像估算了福建省将乐县的杉木马尾松林蓄积量,通过布料模拟滤波算法生成了研究区的数字表面模型、数字高程模型和冠层高度模型,对林分平均高和蓄积量的估测精度分别为94.74%和91.46%;韩宗涛等[3]基于Landsat-8波段信息、植被指数以及地形因子、纹理因子和SAR数据估测了大兴安岭根河地区的森林生物量,通过对比KNN-FIFS法和多元逐步回归方法,发现KNN-FIFS方法估测效果更好(R2=0.77,RMSE=22.74 t/hm2);庞勇等[4]基于机载高分辨率航空影像估测了小兴安岭地区的森林生物量,其基于FOTO算法提取的纹理因子联合多元线性逐步回归方法在估测森林生物量时发现无饱和现象,模型R2达到0.81,RMSE为46.78 t/hm2;严恩萍等[5]基于Landsat5和MODIS数据估测了湖南省攸县森林的碳密度分布,发现Landsat5在碳密度估测时表现更优,估测精度达到82.02%;祖笑锋等[6]基于MODIS产品建立了大区域燃烧生物量模型,其研究方法很好地反映了我国受火灾影响减少的森林生物量;郭云等[7]基于Landsat5数据估测了黑河流域地区的森林生物量,使用ASTER GDEM产品为辅助数据,地形校正能提高生物量的估测精度,在多元线性逐步回归算法下,地形校正前后的R2达到分别为0.31和0.46,RMSE分别为34.41,30.51 t/hm2;戚玉娇等[8]基于Landsat5数据估测了黑龙江大兴安岭地区的森林生物量,发现存在高值低估和低值高估的现象;李亦秋等[9]基于Landsat TM影像和多元线性逐步回归方法估测山东省的蓄积量,其建立的模型估测精度达到87.35%。在国际上,许多学者同样基于遥感数据对森林参数开展了相关估测研究[10-15]。
目前多数研究基于多元线性逐步回归模型方法使用遥感数据估测森林参数,而针对蓄积量饱和点的估测的研究则很少。本文选择湖南省西北部马尾松林为研究对象,对Landsat-8 OLI数据估测马尾松林蓄积量的饱和点进行定量化估测,从根本上了解Landsat-8 OLI数据估测马尾松林蓄积量的能力。此外,基于饱和点估测方法,发展二项式估测模型对马尾松林蓄积量进行建模估测并与多元逐步回归模型进行对比,以期评价二项式模型和多元线性回归模型估测森林蓄积量的能力,为森林资源的快速获取提供新的估测方法。
1 研究区概况
研究区位于湖南省,该区森林资源丰富,尤其是马尾松林 (Pinusmassoniana),在该地区的森林资源中占有非常大的比重[16]。在第八次全国森林资源清查中,湖南省马尾松林的蓄积量占全省森林总蓄积量的14.02%。
2 研究方法
2.1 数据源
2.1.1样地调查数据
地面样地调查在2017年进行,为了保证调查的样地具有代表性,首先对样地的郁闭度进行等级划分:0.20~0.39为第一郁闭度等级;0.40~0.69为第二郁闭度等级;0.70~1.00为第三郁闭度等级。各郁闭度等级分别调查了30,24,18块样地,最终共调查马尾松林地面样地72块。其中,幼龄林样地2块,占比2.78%;中龄林样地26块,占比36.11%;近熟林样地25块,占比34.72%;成熟林样地18块,占比25%;过熟林样地1块,占比1.39%。对所有的样地内胸径大于5 cm的样木进行每木检查,树高测量使用VL5超声波测高器,胸径测量使用胸径尺,获得样地内每株样木的树高、胸径等单木因子。基于蓄积量估测方程计算每株样木的材积,然后求和得到样地尺度的蓄积量,通过尺度扩展,得到调查样地的每公顷蓄积量值。使用GNSS RTK技术对样地和样木进行精确定位,以保证调查数据可以和遥感像元进行精确的匹配。最后,基于样地中心和样木坐标把圆形样地重采至25 m×25 m的样地数据。使用所有的数据进行饱和点计算,在蓄积量估测阶段,把样地数据进行随机分组,70%的样地数据用于建模,30%的样地数据用于模型验证,样地数据具体描述如表1所示。样木材积计算公式如下:
V=0.95682492×D1.8551497×H0.000062341803
(1)
式中:V为材积;D为胸径;H为树高。

表1 样地数据统计信息
2.1.2Landsat-8 OLI数据
Landsat-8 OLI数据基于GEE平台获取,通过GEE平台直接对处理好的地表反射率产品进行提取,该产品为LANDSAT/LC08/C01/T1_SR,为了匹配地面样地调查数据日期,同时兼顾对研究区进行覆盖,产品日期选择20170501—20171031和20180501—20181031。基于该产品的pixel_qa质量属性波段,对该产品进行去云处理,去云处理使用GEE官方公布的方法,直接掩膜掉pixel_qa波段像元属性为3和5的像元。去云后,使用中值函数对覆盖的影像进行中值处理,之后进行重采样(25 m×25 m)和坐标系统匹配。最后,使用地面样地矢量文件对处理好的数据进行波段信息和植被指数提取。其中,波段信息如表2所示。
依据有关研究[17],植被指数选择差异植被指数(Difference Vegetation Index,DVI)、调整差异植被指数(Renormalized Difference Vegetation Index,RDVI)、增强植被指数(Enhanced Vegetation Index,

表2 Landsat-8 OLI波段信息
EVI)、归一化植被指数(Normalized Difference Vegetation Index,NDVI)、绿度归一化植被指数(Green Normalized Difference Vegetation Index,GNDVI)、叶面积指数(Leaf Area Index,LAI)、简单比值植被指数(Simple Ratio Vegetation Index,RVI),各植被指数的具体计算公式如下:
很多时候,换一种说话方式,彼此的心情会截然不同。夫妻相伴多年,更要好好说话,多表达关心,少一些指责,只有这样,那个伴儿才会长久地陪你走下去。
DVI=NIR-Red
(2)
(3)
(4)
(5)
(6)
LAI=3.618EVI-0.118
(7)
(8)
式中:NIR为近红外区反射率;Red为红光区反射率;Blue为蓝光区反射率;Green为绿光区反射率。
2.2 饱和值确定
光谱信息只能反映一定数据变化范围内的森林参数(叶面积指数、蓄积量、生物量、碳储量等),当某一森林参数超出某一范围时,光谱信息并不能对其进行很好的表达,通常把这个临界点定义为饱和点,饱和点是定量化确定遥感数据估测森林参数能力的重要指标。有学者提出基于地统计学模型中半方差函数理论来求解森林生物量饱和点,并用此方法计算了Landsat-8数据估测浙江省森林生物量的饱和点[18]。该模型具体公式为:
(9)
式中:c0为块金常数;c为拱高;(c0+c)为基台值;a为变程。当c0=0,c=1时,称为标准的球状模型。
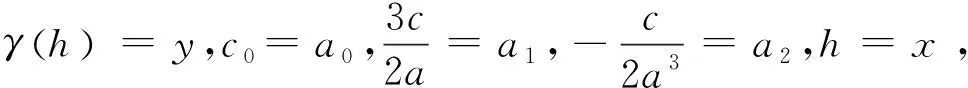
y=a0+a1x+a2x3
(10)
通过对式(10)求解即可得到各参数值。
该简化模型是一种曲线拟合模型,本文尝试提出使用二项式模型进行饱和点求解,并与前人提出的方法进行对比,二项式模型的具体形式为:
y=a0+a1x+a2x2
(11)
式中:y表示波段光谱反射率;x表示蓄积量;a0,a1,a2为模型参数。
2.3 蓄积量估测
确定Landsat-8 OLI数据估测湖南省马尾松林的光谱饱和点后,使用该光谱数据对马尾松林进行建模预测,建模方法选择多元逐步回归方法和基于饱和点确定模型的估测方法,对比2种方法估测马尾松林蓄积量的能力。
多元逐步回归是多元线性回归的一种,其通过逐个对建模变量进行引入,不断剔除对建模结果无意义的变量,最终达到优选变量进行建模预测的目的[19-21]。其原理是:每一步只引入或剔除一个自变量,自变量是否引入或剔除取决于其偏回归平方和的F检验或校正决定系数。如方程中已引入了(m-1)个自变量,在此基础上考虑再引入变量Xi。记引入Xi后方程(即含m个自变量)的回归平方和为SS回归,残差为SS残差;之前含(m-1)个自变量(不包含Xi)方程的回归平方和为SS回归(-i),则Xi的偏回归平方和为U=SS回归-SS回归(-i),检验统计量为(12):
(12)
式中:Fi服从Fα(1,n-m-1)分布。
如果Fi>Fα(1,n-m-1),则Xi选入模型;否则,不入选。从方程中剔除无统计学作用的自变量,过程则相反,但检验一样。
饱和点估测模型是本研究基于饱和点估测方法所提出的蓄积量估测方法,即基于二项式模型对蓄积量进行估测。首先,对建模变量进行相关性分析,得出与蓄积量相关性最大的因子,基于该最相关因子对蓄积量进行建模预测,其模型可表示为:
y=b0+b1x+b2x2
(13)
式中:y表示蓄积量;x表示波段光谱反射率;a0,a1,a2为模型参数。
2.4 模型评价指标
基于模型评价指标[22-24],本文选择决定系数R2,平均绝对误差MAE和均方根误差RMSE作为模型评价指标,具体计算公式为:
(14)
(15)
(16)

3 结果与分析
3.1 波段饱和点
基于SPSS 25.0对Landsat-8提取的波段变量进行皮尔逊(Person)相关性分析,并进行双尾相关性显著检验,结果如表3所示。所有变量均在0.01水平上显著相关,且B3波段与森林蓄积量(FSV)的相关性最好,为-0.625。基于B3变量求解马尾松林蓄积量的估测饱和点,基于球状模型和二项式的模型估测参数如表4所示,得到基于球状模型估测的最大蓄积量饱和点为217.05 m3/hm2(图1红线),基于二项式模型估测的最大蓄积量饱和点为206.86 m3/hm2(图1绿线)。
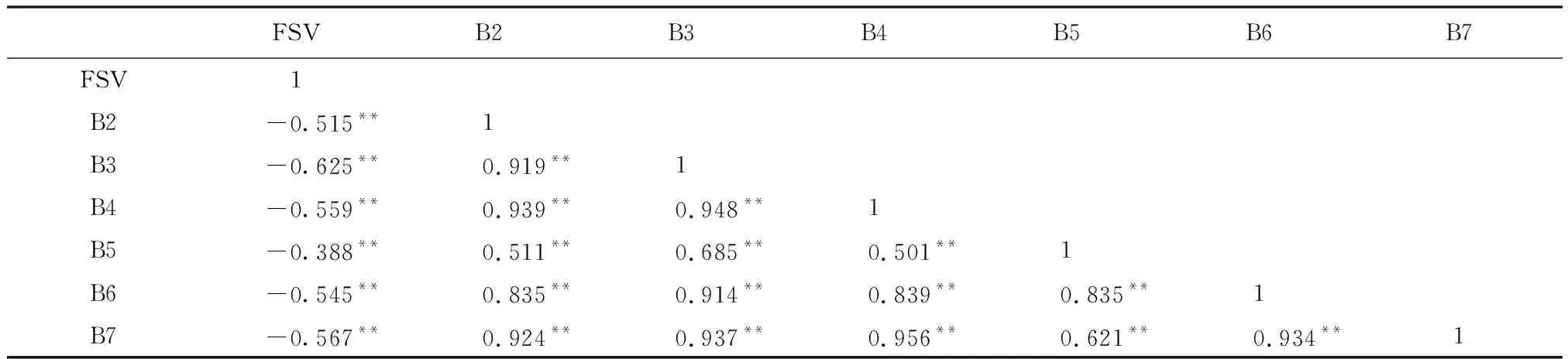
表3 波段变量相关性分析
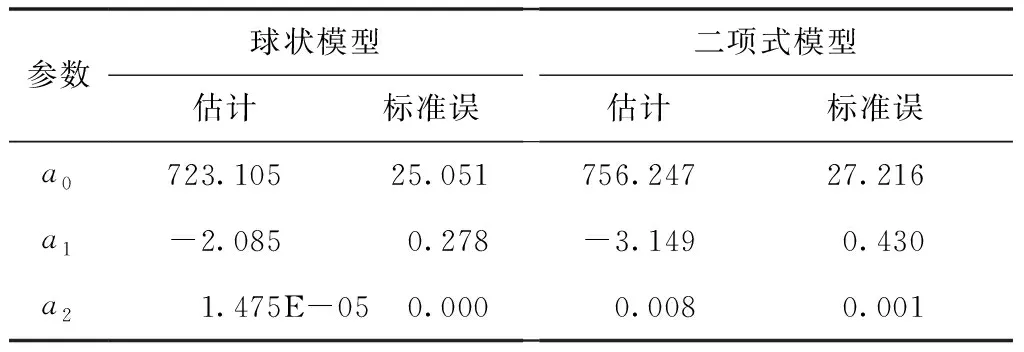
表4 模型估测参数
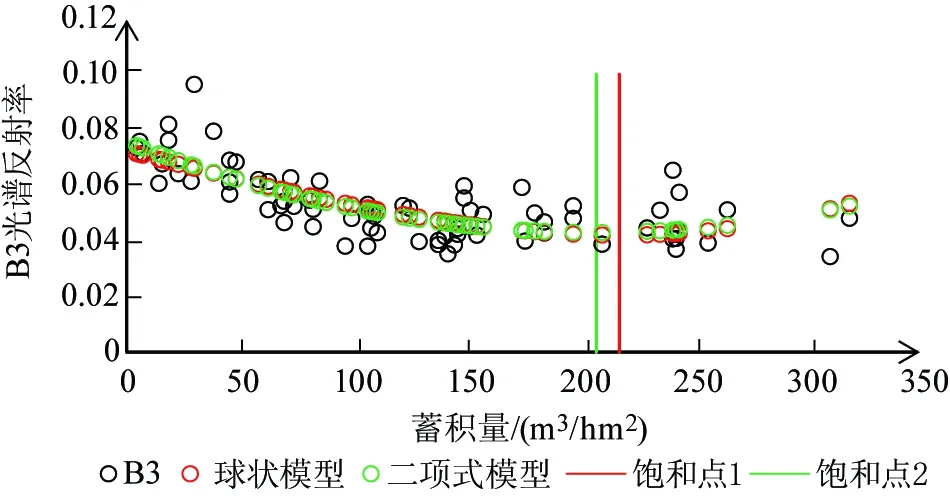
图1 基于B3的蓄积量饱和点确定
3.2 植被指数饱和点
基于SPSS 25.0对Landsat-8提取的波段变量进行皮尔逊(Person)相关性分析,并进行双尾相关性显著检验,结果如表5所示。除了RDVI,EVI和LAI变量与FSV不显著相关外,其余所有变量均在0.01和0.05水平上显著相关,且GNDVI波段与FSV的相关性最好,为0.451。基于GNDVI变量求解马尾松林蓄积量的估测饱和点,方案1和方案2的模型估测参数如表6所示,得到方案1估测最大蓄积量饱和点为196.95 m3/hm2(图2红线),方案2估测的最大蓄积量饱和点为183.06 m3/hm2(图2绿线)。
3.3 基于多元线性逐步回归的蓄积量估测
对随机分好组的建模数据(n=51)进行多元线性逐步回归建模,波段变量和植被指数变量均逐步进入回归模型,建模结果如表7所示。结果表明,与波段信息相比,植被指数在估测湖南省马尾松林蓄积量的表现较差,没有变量进入到预测模型中。显
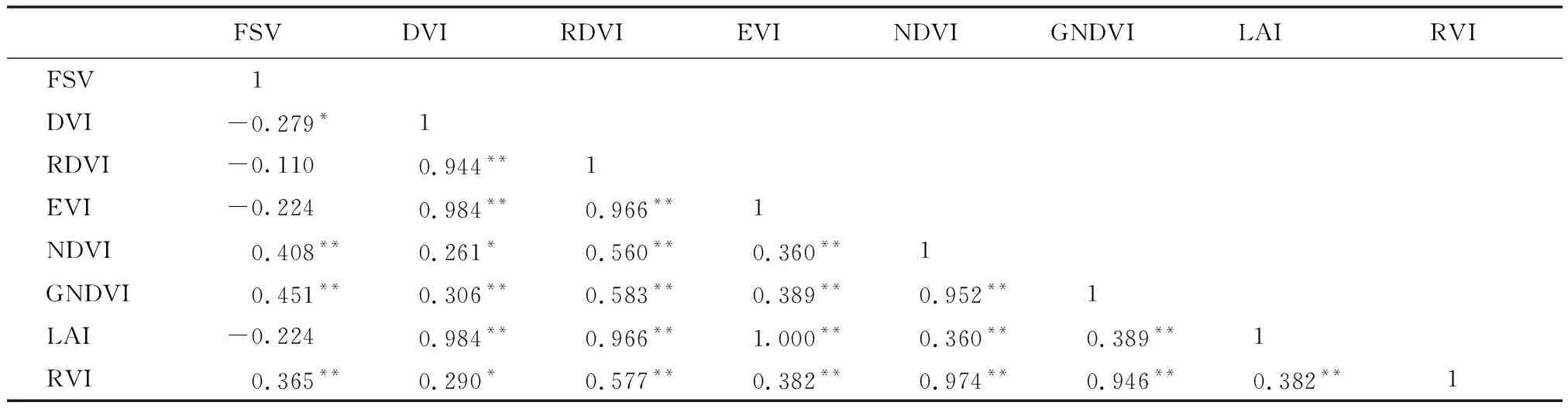
表5 植被指数变量相关性分析
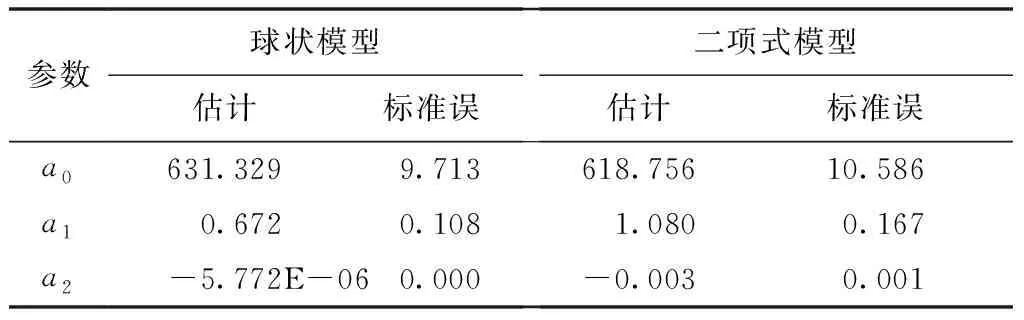
表6 模型估测参数
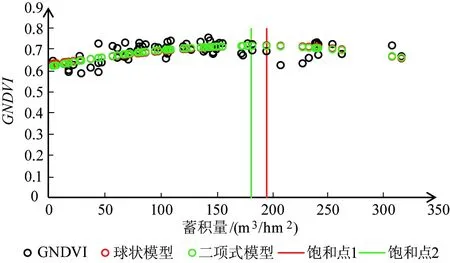
图2 基于GNDVI的蓄积量饱和点确定
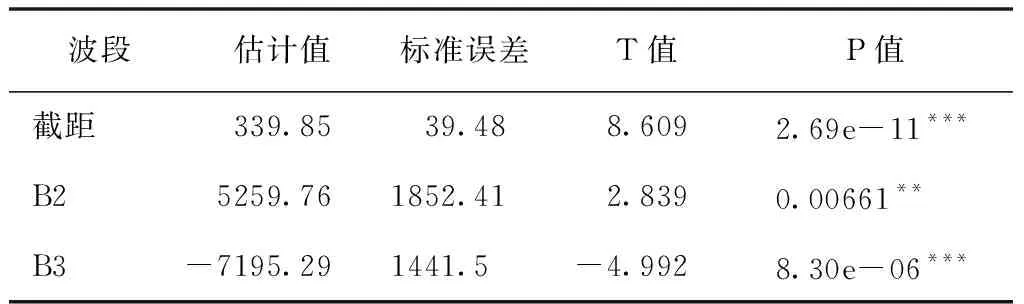
表7 多元线性逐步回归建模结果
著性水平设置为0.05,使用4个自由度的全球检验评估线性模型假设,假设检验全部通过。对所建模型进行精度验证,验证结果如图3所示,模型预测蓄积量值与样地测量值的R2为0.29,MAE为63.35 m3/hm2,RMSE为69.53 m3/hm2。

图3 多元线性逐步回归模型验证结果
3.4 基于二项式(饱和点估测)模型的蓄积量估测
对随机分好组的建模数据(n=51)使用二项式模型进行蓄积量估测建模,建模变量仅选择B3,建模结果如表8所示。对所建模型进行精度验证,验证结果如图4所示,该模型的预测蓄积量值与样地测量值的R2为0.49,MAE为53.76 m3/hm2,RMSE为58.71 m3/hm2。
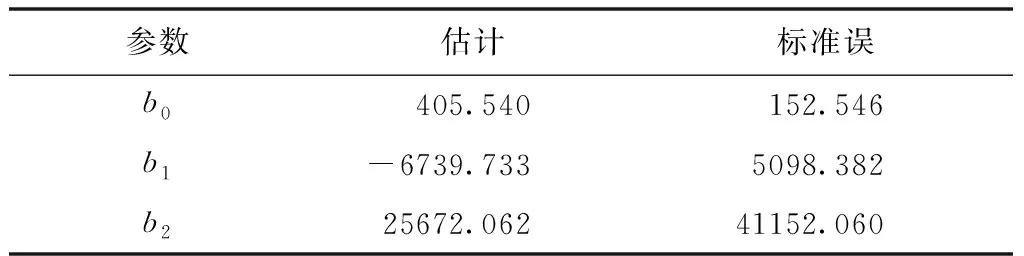
表8 二项式模型蓄积量估测建模结果

图4 二项式模型验证结果
4 结论与讨论
1) 基于本文提出的方法,在对某一区域的森林蓄积量进行估测时,就可以根据其蓄积量的大致分布范围选择适合对其进行估测的遥感数据源。
2) 基于前人研究中提出的基于球状模型的饱和点估测方法,本研究提出的饱和点估测方法更好,原因主要有以下两点:一是球状模型是曲线模型,而二项式模型也是曲线模型,在一定的数据范围内两个数据拟合曲线基本重合,具有较高的相似性,从而在一定程度上具有可比性;二是相较于球状模型,二项式模型对数据的拟合结果更好,在波段信息饱和点估测阶段,球状模型和二项式模型的拟合R2分别为0.53和0.56;在植被指数估测阶段,球状模型和二项式模型的拟合R2分别为0.39和0.43。在蓄积量估测建模阶段,尽管有许多研究基于多元线性回归模型进行森林参数建模预测,本文研究表明基于多元线性回归模型对遥感蓄积量估测研究并不合适(R2=0.29,MAE=63.35 m3/hm2,RMSE=69.53 m3/hm2),即遥感变量与蓄积量并不是一种简单的线性关系,基于二项式模型的单变量估测方法的估测精度更高(R2=0.49,MAE=53.76 m3/hm2,RMSE=58.71 m3/hm2)。
3) 由于湖南省全年受云量的影响,对Landsat-8遥感数据的选择提出了很高的要求,本文使用的Landsat-8数据是基于2017年和2018年2年的数据合成产品,这可能与同一数据源单时相的遥感产品的估测结果存在一定的差异。对特定地区的特定森林类型应进行特定的分析,研究区不同、森林类型的差异对估测结果都会产生一定的影响。

