构造圆解无理方程

江苏省泰州市第二中学附属初中 (225300) 薛晓蓉

本文以部分数学竞赛题为例，谈谈如何构造圆解一类无理方程，供师生教学参考.

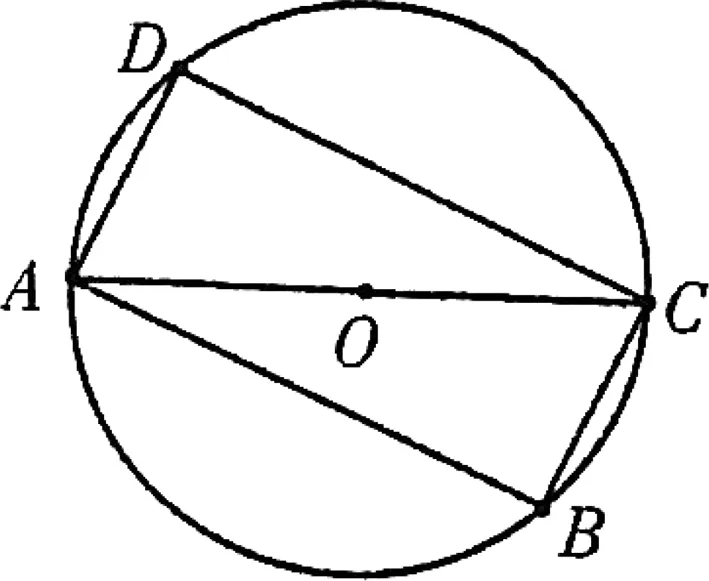
图1

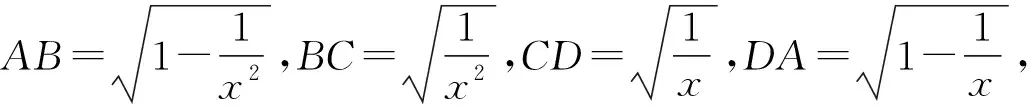
点评：本题如用常规方法求解，则需要两次进行平方，不仅运算量大，而且解题过程繁冗，故不可取，然而通过构造圆，借助于托勒密定理，则简捷明了，富有创意.

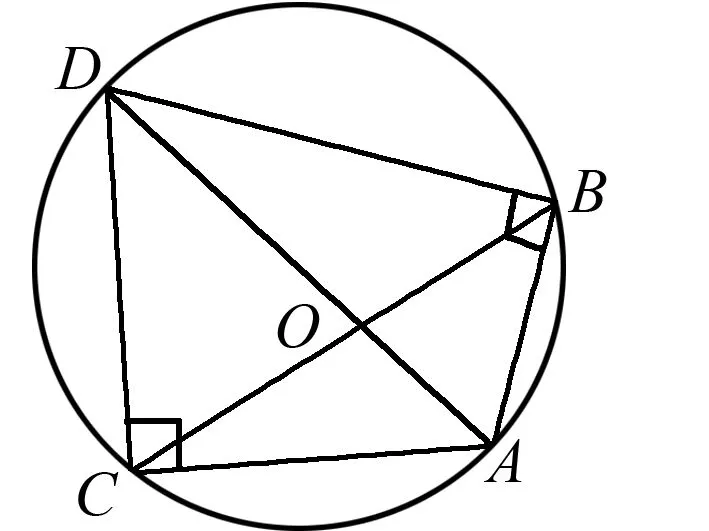
图2

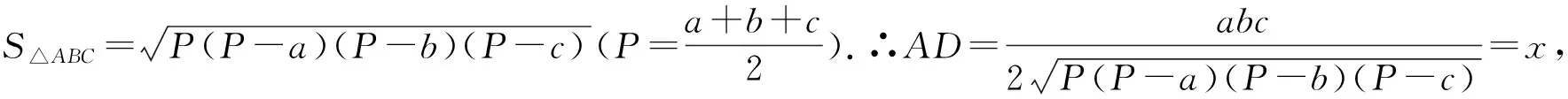
点评：本题由于通过构造圆，借助托勒密定理，结合正弦定理和海伦一秦九韶公式求解，充分显示了构造法的优越性，此法步骤简明，思路明晰，具有创新精神，值得重视.

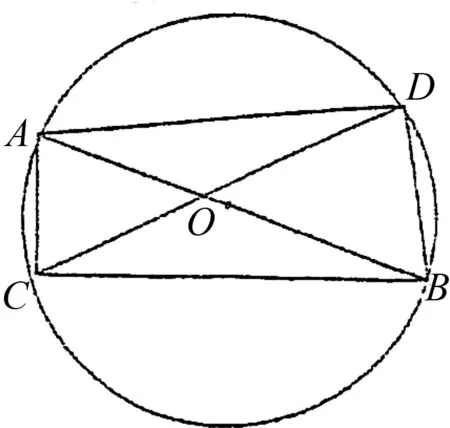
图3

点评：本题比较复杂，如用常规方法求解，将会出现中学生难以求解的一元四次方程，但通过构造圆，借助于托勒密定理和余弦定理，就简捷明了地求得其解，方法新颖，解题快捷，别有风味.

综上所述可知，注意构造圆解无理方程的研究，符合新课程改革关于“让学生的思维活跃起来”的理念要求，有利于提高学生的专题总结水平，有利于学生在研究总结的过程中，拓展视野，启迪思维，有利于学生系统灵活地掌握所学的知识内容，对于帮助学生理解课本内容，培养探索精神和创新意识，提高解题水平和发展思维能力，均颇有益处.

总之，我们要注重教学与培养学生创新能力的研究，要引导学生通过参加专题讲座的探究，使学生更加热受数学，对数学产生浓厚的兴趣，故笔者建议，在今后的教学过程中，对这类专题科研讲座应引起重视，这对于培养学生的探索精神和创新意识，将会起到积极的作用.