注重几何分析巧求解几最值
江苏省新沂市第一中学 (221400) 束峰琛
关于解析几何中的一些最小值与最大值问题,我们可以通过挖掘具体题目中的几何特征,充分运用一些几何图形的性质和相关的几何事实协助解题,这样可以起到优化解题、提升思维品质之功效.本文归纳几个典型题型并分析评注,希望能给读者朋友有所帮助.
一、用对称性
就是运用一个在初中平面几何里已经证明了的几何结论,也是光的折线原理,其核心是通过寻找点关于直线的对称点,变折线段为直线段完成线段和(差)的最值.
例1 已知A(4,1),B(0,4)和直线l:3x-y-1=0,试在l上找一点P,使|PA|-|PB|最大,并求P点坐标.
图1


评注:关于线段和的最小值与线段差的最大值的问题,利用找对称点的方法解决是经济实用的办法,解题中要根据题目要求解答对相应的问题,如求最值或点的坐标.

图2
例2 已知定点A(3,1),试在x轴和直线y=x上分别找点M和N,使△AMN的周长为最小,求此时线段MN所在的直线方程.

评注:三角形的周长就是三个线段的和,如果利用找对称的的方法将三个线段转换到一条直线上,这就是“两点之间,线段最短”,从而解决了最小值问题.
二、用圆的性质
要求关于圆上的动点到定点或定直线的距离最小或最大问题,都是先求圆心到定点或定直线的距离,然后再减去或加上半径达到求最小或最大距离的目的.


评注:解题的思路是先运用三角形的中线长公式将问题进行转化为圆上的动点求最值问题,通过分析圆的几何特征,抓住半径为定值使问题转化为定点与圆心的距离问题.


评注:通过运用圆的性质把两个都动的点的距离问题转化为一定一动的距离问题,这是成功解题的关键.
三、运用圆锥曲线定义
在椭圆、双曲线、抛物线的定义中,有化曲为直及线段和与差的问题,这些也都是解决有关最值问题重要手段,必须注意运用.


图3

评注:在求椭圆上的点到焦点距离问题时,运用椭圆的定义解题是较优化的方法,根据题目的需要还可以将点到焦点距离转化为此点到对应准线的距离,这是统一定义的运用.
例6 已知抛物线方程为y2=4x,直线l的方程为x-y+4=0,在抛物线上有一动点P到y轴的距离为d1,P到直线l的距离为d2,求d1+d2的最小值.

评注:本题是求动点P到定点距离与到定直线距离的和的最值,其解题思路是运用抛物线的定义、结合几何图形分析进行转化求解.
四、注重几何分析
解析几何问题是用代数方法解决几何问题,如果在求解过程中加强几何分析,充分利用几何图形的性质列式解题会使解题过程大大优化,求最值问题也是如此.

图4
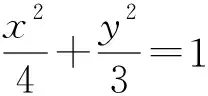

评注:通过几何分析,将求ΔPAB的面积最大问题转化为点P到直线AC的距离最大,再转化为圆心D到直线AC的距离,而此时的点P为直线m与圆D的交点.


评注:在此题求三角形面积的最大值问题中,通过将直线平移转化分析,得到了直线与抛物线相切的极限情况,然后再由判别式法求出了极值点,这是几何分析的成功范例.

