高速铁路轨道几何平顺性计算新方法研究
徐明星 高 贵 李 强 李俊红
(1.中铁四局集团第五工程有限公司,江西 九江 332000;2.武九铁路客运专线湖北有限责任公司,湖北 武汉 430212)
0 概述
目前,国内在建或已开通的铁路客运专线,其设计速度一般为250 km/h或300 km/h,特别是无砟轨道线路,其设计运营速度达到了350 km/h,高速的运营速度必然要求轨道具有极高的平顺性和稳定性。高速铁路具有高平顺性、高安全性、高稳定性、高可靠性及高精确度等特点,在联调联试期间,综合检测列车须通过逐级提速至设计速度的110%来逐级检测轨道几何状态和各项动力性能,其中轨道几何平顺性的检测尤为关键。
长轨铺设放散锁定后,就可以进行长轨精调作业,这是实现轨道高平顺性和高精确度的关键工序之一。长轨精调是采用绝对测量与相对测量相结合的方法,通过轨道几何状态测量仪与全站仪对轨道几何状态数据进行采集测量,结合轨道短波平顺性及长波平顺性要求对采集的数据进行分析处理,模拟计算轨道几何调整量,并以分析结果(长轨精调方案)为依据进行长轨精调作业[4-7]。由此可见,轨道几何平顺性概念在长轨精调作业中居于核心地位。虽然文献对此概念作了详细说明,但是工程实践表明,依据概念计算轨道几何平顺性指标不仅算法复杂、计算量大,而且不便于实际使用。因此在对轨道几何平顺性进行深入研究的基础上,该文提出了一种几何意义明确、计算简单的新方法,并在某高铁工程实践中进行应用,验证了该创新方法的实用性和可靠性。
1 轨道几何平顺性计算新方法
1.1 轨道几何平顺性概念
高速铁路轨道几何平顺性的核心为相对平顺性概念,又具体区分短波平顺性和长波平顺性。
如图1所示,拉1条S=30 m的弦线,以轨枕间距为0.625 m计,每间隔5 m设置1对检测点,则8个轨枕间距正好可以设置一对检测点。以P25与P33为例,此两点间的短波平顺性指标如公式(1)所示[2]。

如图2所示,弦线长度取300 m,每间隔150 m设置一对检测点,则240个轨枕间距正好可以设置1对检测点。以P25与P265为例,此两点间的长波平顺性指标如公式(2)所示[2]。

由上述短波平顺性及长波平顺性概念可知,计算该指标的前提是求得每个检测点在相应弦线下的矢距。以图1为例,首先通过计算确定弦线方程,其次解求每个检测点的设计矢距与实测矢距,最后才可按照式(1)获得检测点对应的平顺性指标。该计算过程较为复杂烦琐,且矢距垂直于弦线,而钢轨平面精调时为沿线路法向移动,即垂直于图1中的曲线,两者之间的几何意义不一致[2],这就是工程建设实践中易引起混淆的原因。

图1 短波平顺性示意图

图2 长波平顺性示意图
1.2 优化后的平顺性计算模型
将式(1)及式(2)进行优化可得出新的算式,如公式(3)所示。

该差值与P25相对于线路的法向偏移量存在明确的几何关系,如图3所示。
如图3所示,A点为偏离设计线路位置的某一实测点,该点与设计线路的法向交点为D,设点D处的曲率半径为R并作圆,其圆心为O;在该圆上作弦线S,然后过A点向弦线S作垂线,与弦线S相交于C,与圆相交于E。由图形可见,AC为实测矢距,EC为设计矢距,AE为A点处的矢距差,AD为该点处的法向偏移量,AE与AD间的夹角为θ[4-7],则AE与AD间的微分几何关系为及其差值Δ为:

且由图形关系可知,θ的变化范围与弦线S及半径R相关,其取值区间为[0~arcsin(S/2R)]。根据规范取AD的极限值为10 mm,则在不同的半径值下,以30 m及300 m作弦线,矢距差与法向偏移量的差值Δ及角度θ的变化情况见表1。
由表1可见:在30 m弦线情况下,即使半径取500 m,矢距差与法向偏移量的差值Δ的极大值也仅为0.004503 mm;在300 m弦线情况下,500 m半径对应的Δ极值为0.482848 mm,随着半径的增大,该值急剧缩小。由于高速行车对线路选线的要求,曲线半径的取值不能很小,因此在数值上可认为矢距差与法向偏移量是等同的,因此对式(3)进行优化,将矢距差替换为法向偏移量,得到算式,如公式(5)所示。

用式(5)减去式(3),则得平顺性指标在2种算法下的较差,设i、j点的法向偏移量分别为σi、σj,对应的角度分别为θi、θj,可得较差的理论计算如公式(6)所示。

仍以10 mm为法向偏移量的极值,则式(6)在θi取极大值,θj=0时取得最大值。在不同半径下并以30 m及300 m作弦线,对ΔH的极大值所做的数值分析结果与表1相同。因为短波平顺性与长波平顺性的限差分别为2 mm及10 mm,ΔH与之相比仅为微小量可以忽略不计,因此完全可以采用式(5)代替式(3)进行轨道几何平顺性的计算。

表1 矢距差与法向偏移量的差值Δ及角度θ的变化情况表
1.3 法向偏移量计算模型
由上述分析可知,采用式(5)计算轨道几何平顺性指标的好处在于几何意义明确,便于理解,其使用前提则是必须先计算法向偏移量。轨道线路设计线型有3种,分别是直线、缓和曲线及圆曲线,与之对应,法向偏移量也有3种计算模型[1-7]。1)直线地段的法向偏移量较容易计算,在确定直线方程以后,解求过检测点且与已知直线垂直的另一直线,2条直线的交点与检测点间的距离,即为检测点的法向偏移量[1]。2)圆曲线地段的法向偏移量计算方法是解求检测点与圆心的连线跟圆曲线的交点,则交点与检测点间的距离即为法向偏移量[1]。3)缓和曲线地段的法向偏移量可基于缓和曲线的参数方程[3]较为方便地求得某一检测点的法向偏移量。

图3 矢距差与法向偏移量几何关系示意图
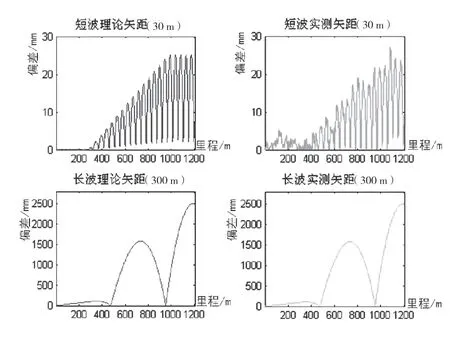
图4 长短波设计矢距与实测矢距分布图

图5 长短波矢距差与法向偏移量之差值分布图
2 数据对比分析
以某高铁无砟轨道约800 m实际轨道静态检测数据为例,首先计算长波与短波的设计矢距与实测矢距值,解算结果如图4所示;其次解算每个检测点的法向偏移量,并与长短波矢距差进行比较,比较结果如图5所示;再次,在获得矢距差及法向偏移量的基础上,即可计算长短波平顺性指标,2种算法所获得的长短波平顺性及其差值情况如图6所示。
对比分析图4、图5及图6可知以下4点:1)短波矢距值的量级可达到cm级,而长波矢距值的量级可达m级,短波理论矢距值的最大值从0逐渐增加到一个定值,表明该段轨道的线形从直线进入缓和曲线并最终进入圆曲线;虽然从整体上看,理论矢距波形图与实测矢距波形图有相同的走势,但是短波理论矢距图与短波实测矢距图在细节上的不吻合较长波更明显,因此可初步判断该段轨道的短波平顺性不理想。2)理论分析表明,矢距差与法向偏移量在直线段有相同的几何意义,其数值相等。如图5所示,无论长波还是短波,矢距差与法向偏移量之差值在直线段为0,而在曲线段有一个微小量,其中短波差值的分布区间为-0.1 mm~0 mm,长波差值的分布区间为-0.05 mm~0.05 mm。3)由于矢距差及法向偏移量所计算的长短波指标在直线段数值相同,在曲线段有微小差异,因此两种算法所得之平顺性波形图呈现几乎一致的走势,由于长短波平顺性的合格指标分别为10 mm及2 mm,而短波平顺性差值的分布区间为-0.1 mm~0.1 mm,长波平顺性差值的分布区间为-0.05 mm~0.05 mm,与合格指标相比完全可以忽略不计,因此也表明可以采用法向偏移量代替矢距差来计算轨道几何平顺性。4)如图6所示,该段轨道短波平顺性存在部分超限点,则说明需要进行长轨精调作业。精调采用相对性调整的原则,即只要平顺性指标满足规范要求则可,不苛求轨道实际位置与设计位置严格一致。

图6 2种算法所得之平顺性性波形及其差值分布图
3 应用效果评价
某高铁运用该文研究的新方法进行轨道几何平顺性指标计算,并指导开展了长轨精调作业,在联调联试、动态检测和运行试验阶段,通过轨道综合检测列车对线路的逐级提速检测测试,并对轨道几何状态进行了分析评价,根据数据显示,采用该文研究的新方法进行轨道几何平顺性指标计算,取得的效果显著,最终应用效果评价数据如下。
3.1 局部峰值评价
某高铁上、下行正线各检测验收100 km,均无验收II级偏差,3 km含有验收I级偏差,每公里线路出现单项验收I级偏差长度≤5%,按照整公里为单位进行验收评价,参与检测验收的100 km全部满足局部峰值验收标准要求。
3.2 区段均值评价
某高铁上、下行正线平均TQI值均为1.7 mm,其中无砟段平均TQI值均为1.6 mm;上、下行正线均未出现TQI验收I级 和II级偏差,参与验收的区段全部满足区段均值验收标准要求,取得了较好的效果。
4 结语
在高速铁路建设中,长轨精调作业是建设高平顺性轨道的关键一步,其核心技术即是平顺性指标的计算。该文通过深入研究几何平顺性的计算理论、数据分析处理和实践运用,得出如下结论:1)该文提出的轨道几何平顺性指标计算新方法更容易理解,几何意义更明确、计算方法简单,实用性更强。2)某高铁无砟轨道线路运用该计算方法指导了长轨精调,静态调整平均轨道质量指数(TQI)达到了1.26 mm;根据动态检测报告对某铁路正线轨道几何状态的评价结果显示,无砟轨道平均轨道质量指数(TQI)值达到了1.6 mm;均未出现TQI验收I级和II级偏差,全部满足区段均值验收标准的要求,进一步说明该方法及其主要结论能够应用于高速铁路无砟轨道的建设实践。3)该文提出的轨道几何平顺性指标计算新方法可以很好地指导长轨精调作业,减少了长轨精调的遍数,缩短了长轨精调的工期,进而节约了施工成本,极大地提高了施工功效,具有广阔的应用前景和推广应用价值。

