不同纤维方向角时碳纤维增强树脂基复合材料切削力建模

秦旭达 朱圣富 李士鹏 葛恩德 唐心凯

（1 天津大学机构理论与装备设计教育部重点实验室，天津 300350）

（2 上海飞机制造有限公司航空制造技术研究所，上海 201324）

文 摘 碳纤维增强树脂基复合材料（CFRP）切削中，存在纤维断裂、基体失效和界面相失效等多个过程，且不同纤维切削角时切屑形成机理不同，因而CFRP切削力的有效预测非常困难。对此本文结合最小势能原理和Winkler弹性地基梁理论，基于CFRP代表性单元（RVE），利用其微元求解纤维挠曲变形方程，分别分析了不同纤维方向角时三个切削变形区的力学行为，并完成纤维临界损伤长度的预测，最终形成不同纤维方向角时的CFRP 切削力解析模型。通过CFRP 直刃铣刀铣削实验，进行了切削力模型的验证，当纤维方向角在0°～180°时，切削力计算值和实验值随纤维方向角的变化趋势相吻合，切削力大小误差在15%以内。切削力随纤维方向角的增大先增后减，分别在90°和45°附近转变变化趋势。切削形貌表明，纤维方向角为135°时，CFRP铣边加工质量较差，临界损伤长度也较大。建立的切削力解析模型可以较为准确地预测CFRP正交切削力，可为CFRP切屑形成中的力学行为分析提供理论指导。

0 引言

碳纤维增强树脂基复合材料（CFRP）具有可设计性强、比强度高和耐腐蚀优越，使得在航天航空、船舶和汽车等领域的应用越发广泛［1］。为满足CFRP构件的装配尺寸精度要求，常需进行微小尺寸的铣削加工［2］。然而，CFRP 多相性和各向异性的特征导致其加工过程与金属相比有很大的不同，存在纤维断裂、基体失效和纤维-基体间界面失效等多组分的不同失效去除过程，极易产生表层的撕裂、凹坑、分层与面下微裂纹等损伤［3］。同时纤维方向角对切屑形成过程有巨大影响，因此CFRP 切削过程中不同组分的力学行为分析极为复杂［4］。

针对上述提及的问题，国内外学者进行了持续且深入的研究。张厚江等［5］基于直角切削实验的观测，将CFRP切削区划分为三个变形区，给出了纤维方向角为0°～90°的切削力计算公式，但适用范围较窄且精度不高。吴红等［6］用硬质合金铣刀对CFRP进行铣削实验并对实验数据进行回归分析，建立铣削力经验公式，但拟合得到的经验公式需要实验数据较多且未考虑到纤维方向角的影响。XU等［7］将纤维周围材料作为等效均质材料处理，考虑切削速度建立CFRP单纤维力学模型，给出其切削力预测公式，但未把基体和界面相的影响考虑进去。贾振元等［8］同样建立单纤维切削模型，分析纤维和树脂所受约束和界面温变特性对切削力计算精度的影响，并使用宏观切削力来对单纤维切削模型间接验证，但未对刀具参数和不同加工变形区的影响加以分析。VOSS等［9］基于最小势能原理和实验数据得出了切削力模型，实测加工过程中的刀具几何参数，获得了切削力与刀具参数和加工参数之间的关系，但对不同纤维方向角的切削力和切削机理的分析并不够全面。

本文在考虑刀具参数的情况下，对0°～180°的纤维方向角进行分类讨论，将切削区域划分成三部分。对切削过程中纤维、界面相与基体组成的一种代表性单元（RVE）进行受力分析，基于最小势能原理和Winkler 弹性地基梁理论，解出RVE 挠曲变形方程并求得其切削力计算值。设计硬质合金直刃铣刀铣边加工CFRP 单向板实验，利用SEM 观测加工区域，从而验证临界损伤长度变化规律和建立的切削力学模型，拟为CFRP 的切屑形成过程中力学行为分析提供理论指导。

1 CFRP切削力学模型

1.1 CFRP切削力学过程分析

CFRP 在宏观上表现出各向异性，在细观上呈现出三相混合态，其切削加工过程从细观尺度的纤维断裂与基体及界面相的开裂开始，随刀具持续进给最终沿刀具前刀面发展成切屑。各向铺层相同的CFRP 是构成多向铺层的基本单元，纤维铺层方向定义为纤维方向角θ［10］。

由于切削加工环境与刀具几何参数和加工参数之间的关联性，为方便进行后续的宏细观力学分析，做出如下假设：（1）变形一致；（2）纤维断裂在其最大拉应力达到拉伸强度时；（3）纤维在破坏之前发生弹性变形，树脂不存在拉压变形；（4）不计纤维和树脂因泊松比不同在纵向受力时导致横向变形不同的影响；（5）切削温度对加工性能的影响只做温度常系数考虑［11］。

基于实验观测，对单向CFRP 在切削过程中的受力变形进行分析，划分的三个区域组成切削力来源，分别为I切屑滑移区、II纤维树脂断裂区和III后刀面回弹区。在CFRP 切削加工过程中，纤维方向角和刀具前角γ不同，会导致切削区域存在不同的受载形式，出现不同的损伤形式，得到不同的切削力大小，如图1所示。

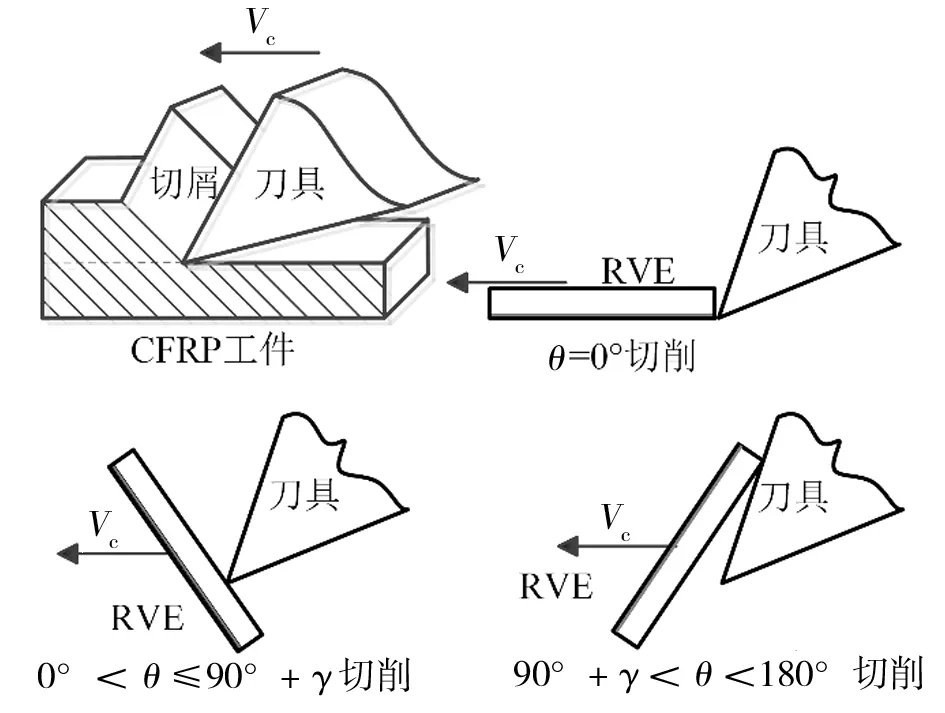
图1 CFRP切削状态分析Fig.1 Cutting state analysis of CFRP

1.2 θ=0°时切削力建模

当θ=0°时，切削方向和纤维轴向呈平行关系，较低的树脂破坏强度使得在切削加工中，达到纤维基体的结合强度，纤维从复合材料基体剥离形成切屑，在切断部分纤维时，存在挤压作用，刀具和RVE接触建立如图2所示的分析模型。

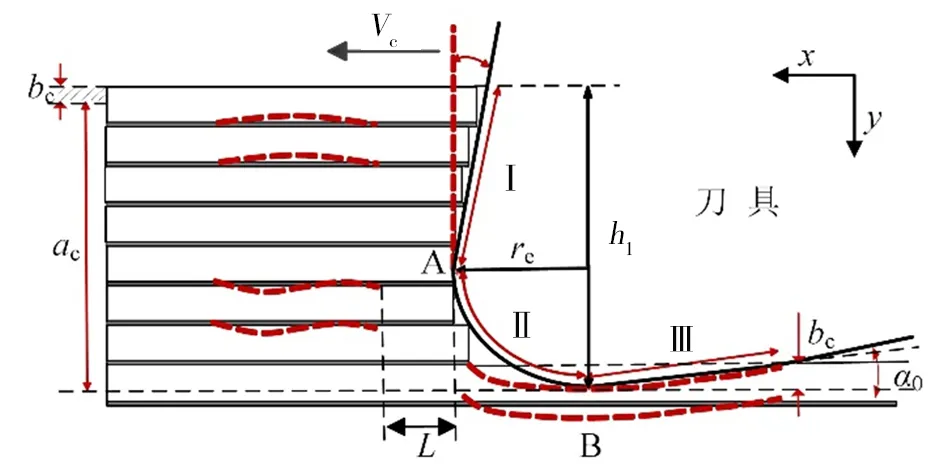
图2 CFRP在θ=0°时切削模型分析Fig.2 Analysis of cutting model when θ=0°

记刀具的进给速度为Vc，在切削过程中涉及几何参数：刀具刃口半径re，刀具前角γ0，刀具后角α0，切削深度ac和加工后RVE 的回弹高度bc。定义刀尖圆弧与RVE 的接触点为A，其切削深度位置为B，若每次加工后已加工表面的回弹高度认为是一致的，则区域I处的高度范围h1为：

1.2.1 切削滑移区的切削分力

区域I：在弯曲外载荷的作用下，当纤维所受到的应力达到细观弯曲强度时，RVE发生弯折劈裂，去除形成宏观切屑，定义细观弯曲强度σmb作为一个综合的失效判据，用以求得切削滑移区所受到的切削分力［12］：

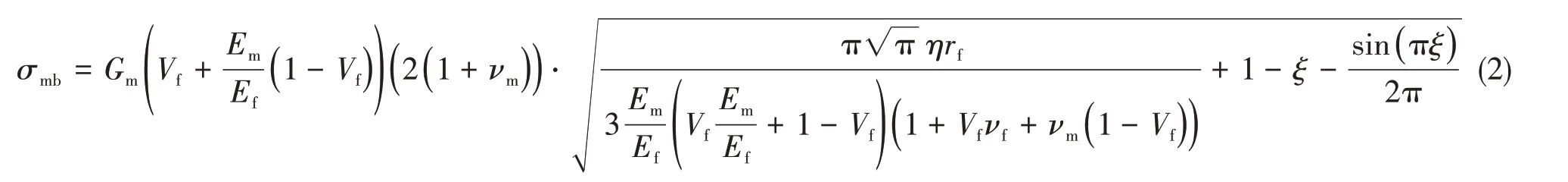
式中，Gm为基体的剪切模量，Em为基体的弹性模量，Ef为纤维方向的弹性模量，νm为基体的泊松比，νf为纤维的泊松比，Vf为纤维的体积分数，rf为纤维的半径。同时对RVE滑移程度的描述用ξ来表示，η表述了RVE与周围材料的约束状态，取值ξ=0.02，η=1.98［13］。

对刀具进给过程分析可知，刀具前刀面作用在与其成γ0角度的投影面上的作用力，即为区域I处的RVE 失效力，大小为细观弯曲强度与其投影作用面积的乘积，若以平均力作为考虑，乘上修正系数K=0.5；同时考虑摩擦，可得区域I处的切削分力为：

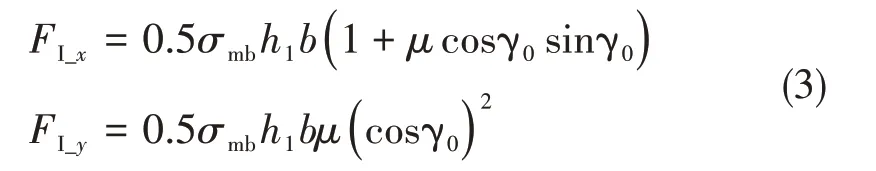
1.2.2 纤维树脂断裂区的切削分力

对区域Ⅱ所在的圆弧AB段而言，主要形成纤维基体的脱粘，其次是纤维的弯折和树脂的压溃。刀具与RVE之间的作用力当集中力处理，其接触区域可以看做半无限长的地基梁，RVE受到与其垂直的切削力Fy以及界面相的粘结力Pi作用而发生弯折，故其变形与半无限长杆件的挠曲变形类似，如图3所示。

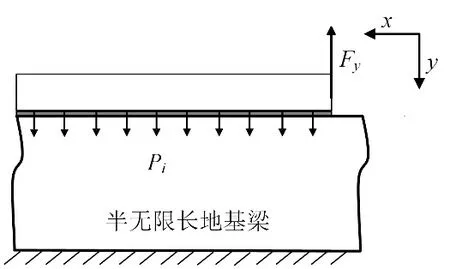
图3 半无限长的地基梁等效切削Fig.3 Equivalent cutting of semi-infinite foundation beam

利用能量原理求解其挠曲方程，被周围材料包裹的RVE存在以下四部分能量：纤维弯曲的弹性应变能Uf、基体的剪切应变能Um、与RVE垂直的切削力所做的功WFy以及界面粘结力所做的功WPi，该总能量表示为：

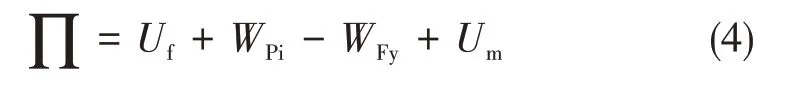
利用Winkler 的地基梁模型原理，RVE 周围材料的界面粘结力Pi的计算表达式为［14］：

式中，ki为纤维层与基体粘接层的等效模量，记半无限长地基部分厚度为无量纲数n，取n=1.66［15］：

该RVE系统整体势能之和为：

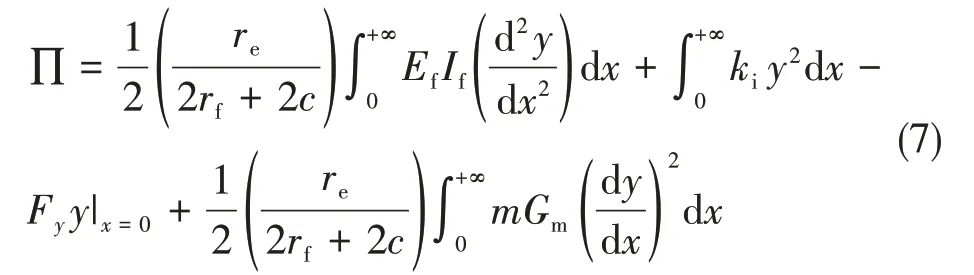
式中，If为纤维的截面惯性矩，且有：

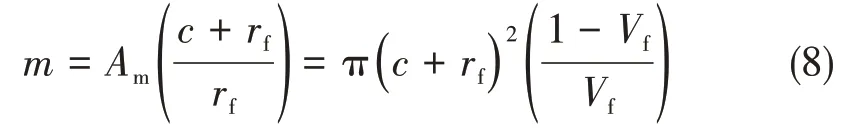
式中，Am的大小是代表单元中基体材料的横截面积，c为RVE中基体厚度的一半，如图4所示。

由最小势能原理可知，一个系统总是会在其总势能最小的状态下保持稳定，因此令式（7）中总势能的一阶差分等于零：

图4 RVE截面示意图Fig.4 RVE section schematic

进行数学整理和计算后，得到切削过程中RVE的挠度微分方程：

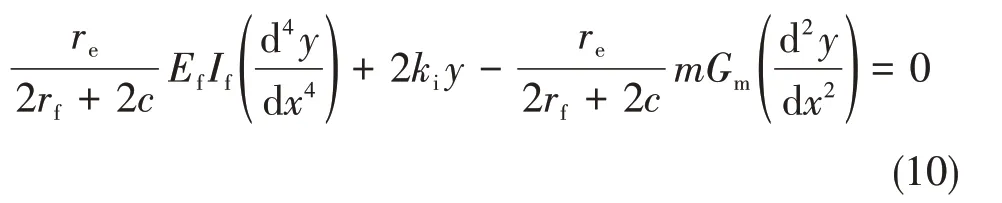
对四阶线性非齐次微分方程式（10）求解，得到如下的RVE弯曲的挠度通解：

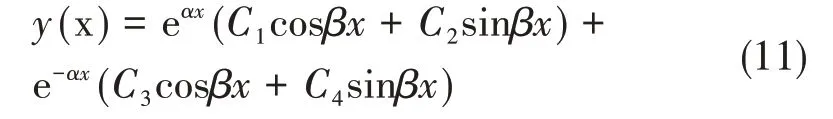
式中，C1～C4均为积分常数，且有：

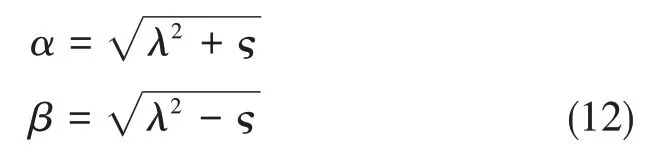
式（12）中：

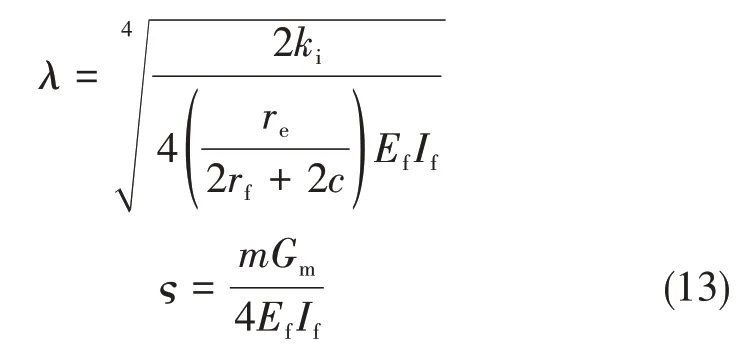
RVE与刀具接触后的变形边界条件为：

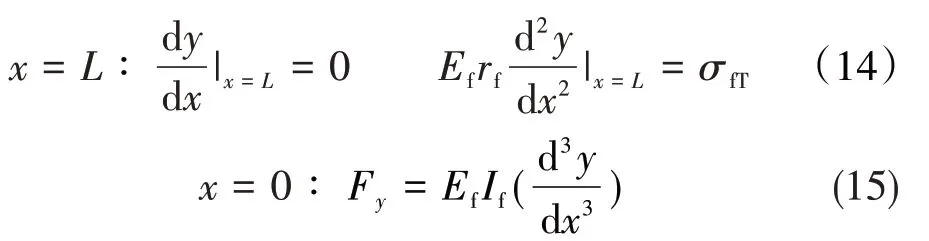
实际加工过程中无穷远处的纤维挠度等于零，可得积分常数C1=C2=0，根据上述边界条件可得积分常数C3、C4的表达式。

因纤维抗拉能力弱于抗压能力，当RVE 的最大拉应力达到纤维拉伸强度极限时，纤维失效弯折断裂，同时此临界值满足界面发生脱粘失效的条件：

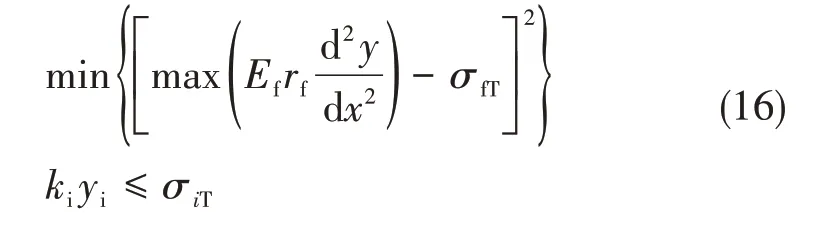
式中，σfT为纤维拉伸强度极限，σiT为界面粘结强度，利用（16）式可以确定失效时的临界损伤长度L和纤维挠度y。考虑摩擦时区域Ⅱ处的切削分力为：

1.2.3 后刀面回弹区的切削分力

区域Ⅲ的后刀面作用于工件材料的压力为N，如图5所示，其看作是二维钝楔作用在平面上的一部分区域［16］，刀具后刀面和加工面回弹区域的接触长度为Lp。

利用接触力学分析可知，接触区域的法向压力在接触边界时压力一定降为零，故得后刀面压力N：

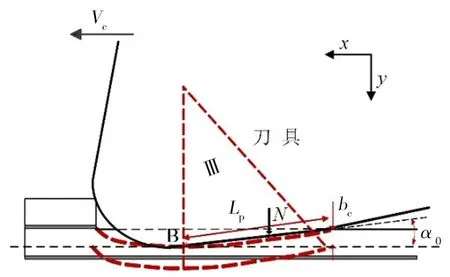
图5 后刀面与加工回弹区接触Fig.5 Contact of back cutter face and processing rebound area

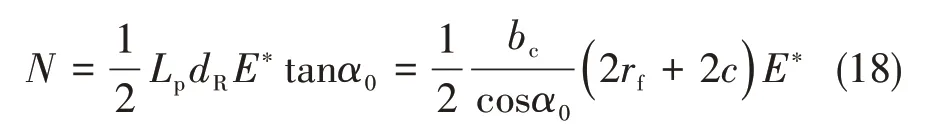
式中，E*为接触变形区的等效弹性模量，其计算公式：

式中，Et、νt分别为刀具的弹性模量和泊松比，ER、νR为加工后复合材料的弹性模量和泊松比，故在后刀面回弹区因后刀面接触而产生的切削分力为：

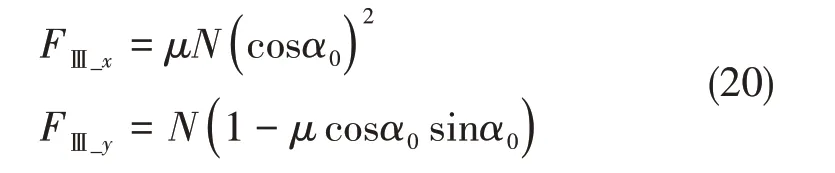
区域Ⅱ和区域Ⅲ所讨论的是纤维和界面及基体组成的RVE单元的切削过程，考虑到在区域I处的切宽为b，故综合三个区域的作用力可得：

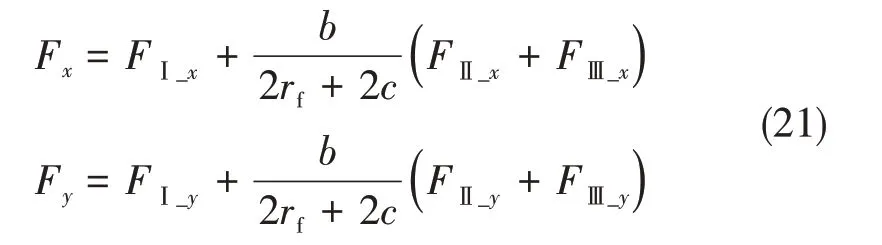
1.3 0°<θ≤90°+γ时切削力建模

刀具进给时先与区域Ⅱ接触，随着θ的增加，接触点A不断上移，使得RVE与前刀面的接触面积增大，切削过程中主要发生挤压切断，在纤维垂直方向及剪切应力作用下的顺纤维方向产生粉状切屑。当θ=90°+γ时，刀具前刀面与纤维方向平行，此时刀具和纤维的接触面积达到最大，简化后建立如图6所示。

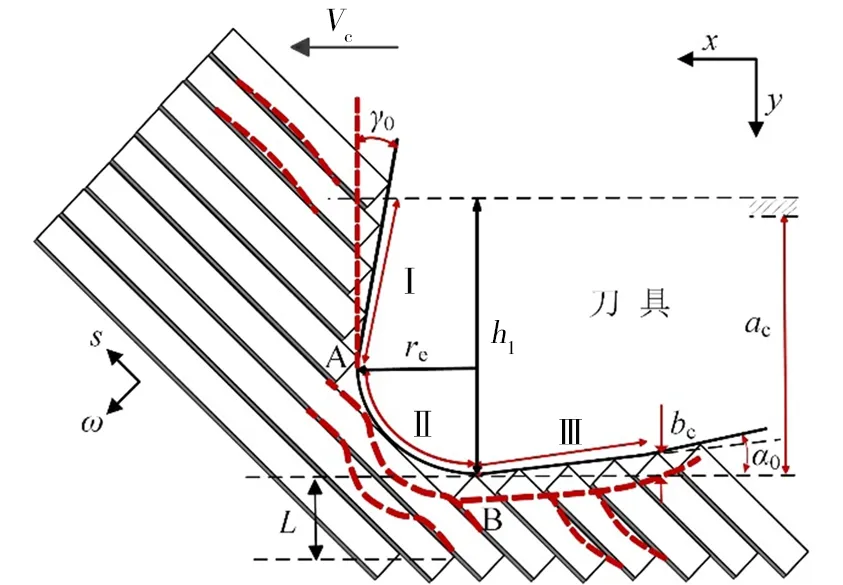
图6 CFRP在0°<θ≤90°+γ时切削模型分析Fig.6 Analysis of cutting model when 0°<θ≤90°+γ

1.3.1 切削滑移区的切削分力

在区域Ⅰ处主要发生垂直于纤维方向的纤维的断裂和平行纤维方向的树脂的滑移与压溃，受到滑移剪切力的作用，记其层间剪切强度为τs，则区域Ⅰ处所受的滑移剪切力为：

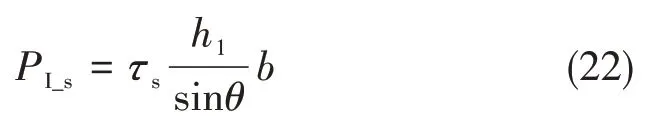
考虑摩擦时区域I切削分力为：

1.3.2 纤维树脂断裂区的切削分力

对图6所示的区域Ⅱ而言，选取刀尖和RVE 接触点A 建立其局部坐标ω-s进行分析计算。在刀具对RVE 的剪切挤压过程中，其受到外力F，未加工侧材料的支撑约束力Ph及粘结约束力Pi的共同作用，取B 点下部的未开裂破损部分，宽度为ds的微小单元体进行受力分析，其受力如图7所示。

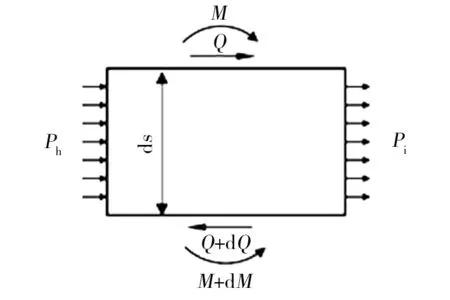
图7 微小单元受力分析Fig.7 Stress analysis of micro-element

周围材料的支撑约束力Ph是作用于RVE的分布力，故由Winkler弹性地基梁模型原理可知：

式中，kh为周围材料的支撑参数，作用方式系数C取值为1.13，其值通过Boit’s公式计算得到［17］：

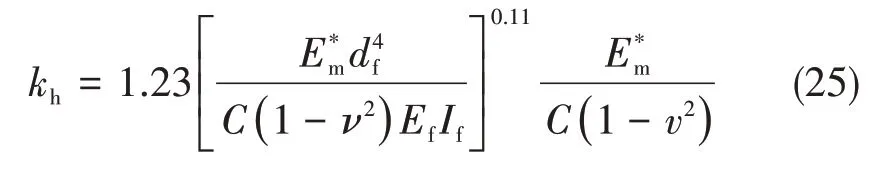
将式（5）和式（24）代入图7中所示微小单元的受力平衡关系中，可以得到力与弯矩的平衡公式：

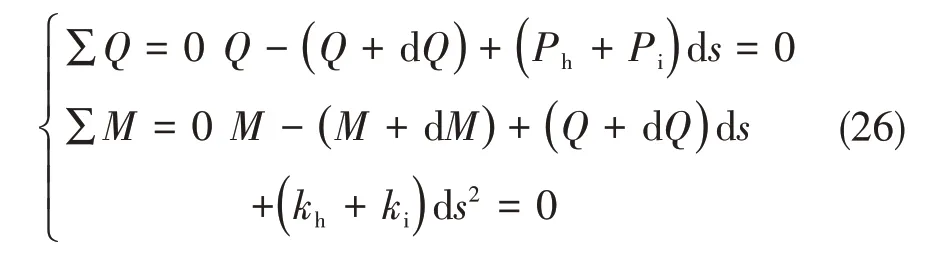
式中，Q为无穷小单元所受的剪切力，M为无穷小单元所受弯矩，根据梁弯曲理论可知：

对式（26）中的二阶微分变量进行简略，代入式（27）后化简可得RVE的变形控制方程为：

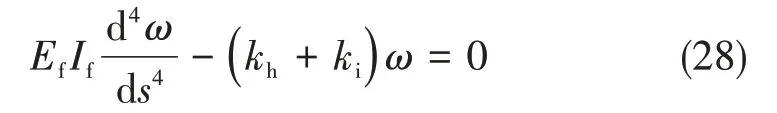
对式（28）求解可得RVE的挠度通解为：

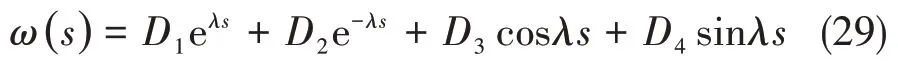
上述通解中，D1～D4均为积分常数，同时有：

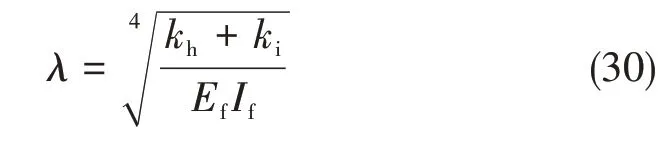
对RVE的变形分析可知其满足以下边界条件：

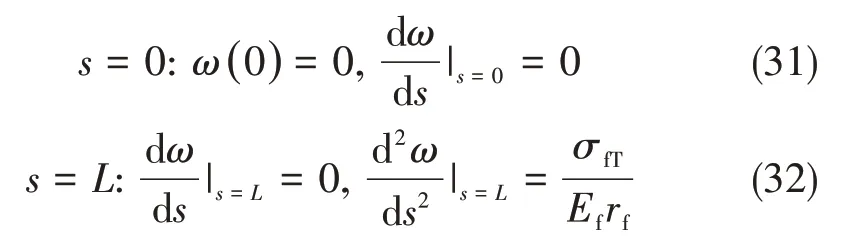
同理，临界值满足界面发生脱粘失效的条件：

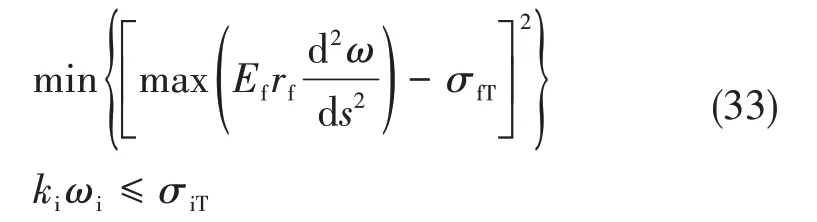
根据图6中几何关系可知，RVE在其长度方向上存在多种支撑条件，划分为临界损伤终止点上部和下部，求解叠加可得RVE所受的切削力：

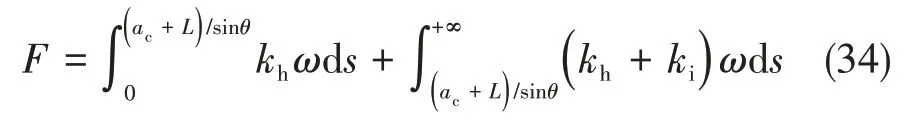
考虑摩擦时区域II处的切削分力为：

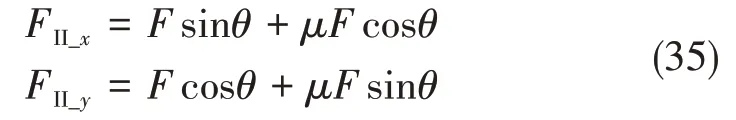
1.3.3 后刀面回弹区的切削分力

刀具的后刀面和纤维树脂的接触形式与平行切削的情况类似，故在后刀面回弹区因后刀面接触而产生的切削分力为：

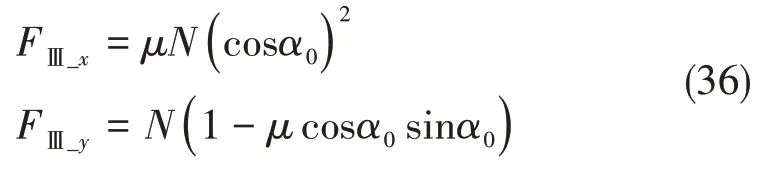
综合以上三个区域切削分力叠加后可得：

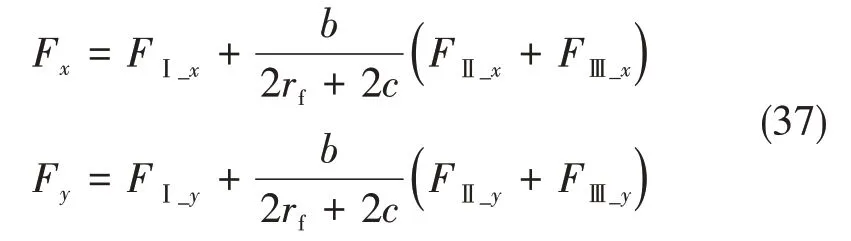
1.4 90°+γ<θ<180°时切削力建模

加工区域的CFRP 去除形成切屑时，后刀面产生的回弹力较前刀面及刀尖钝圆处的挤压力来说可以忽略不计，故可得其接触分析如图8所示，此时弯折断裂成为RVE 的主要断裂形式，当纤维的弯曲应力大于其弯曲极限时，断裂形成切屑，树脂的破损也主要是弯曲应力导致的，一般切削平面下部出现断裂点。

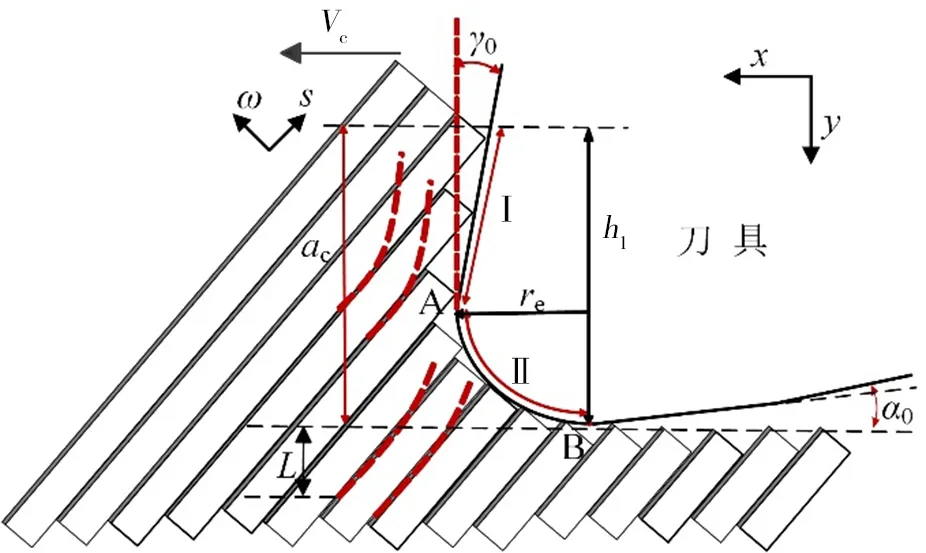
图8 CFRP在90°+γ<θ<180°时切削模型分析Fig.8 Analysis of cutting model when 90°+γ<θ<180°

1.4.1 切削滑移区的切削分力

对区域I 纤维的挤压力和纤维与树脂之间剥离的作用力，使其成为纤维断裂和切屑滑移发生的主要区域。由于RVE 的主要失效形式为弯断，且纤维变形引起的应力与弯矩之间的关系为：

根据材料力学的知识可知，纤维的最大应力发生在纤维半径rf处，且纤维的弯曲应力达到纤维的弯曲强度之后，纤维开始出现弯断失效，则有：

同理，建立其局部坐标ω-s进行分析计算，得到RVE的变形控制方程为：

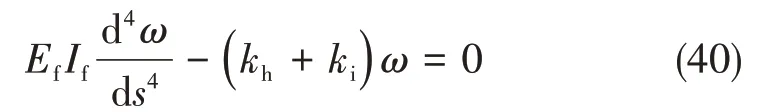
式中，E1～E4均为积分常数，且挠度通解为：

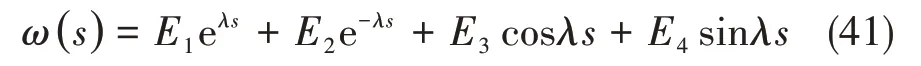
对RVE 的失效变形分析可知其满足以下边界条件：

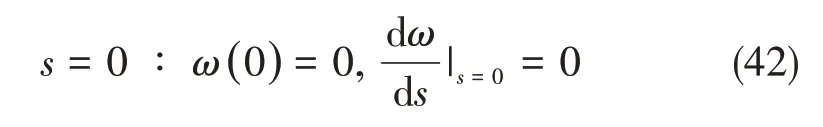
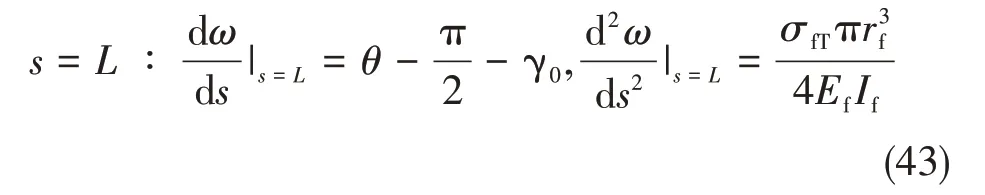
其最大拉应力满足界面发生脱粘失效的条件：

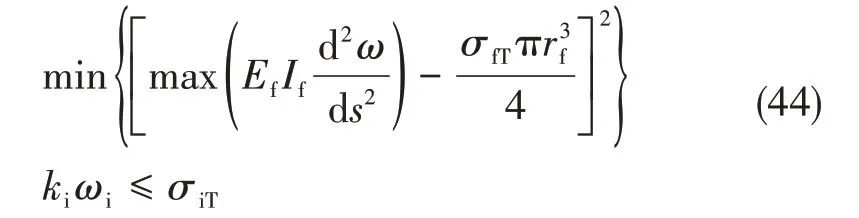
根据图8中几何关系可知RVE所受的切削力：

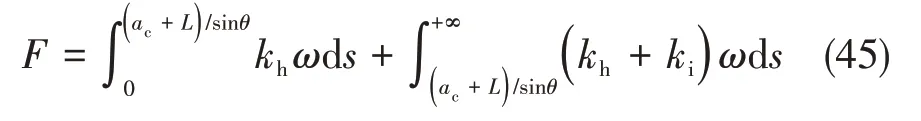
同时考虑摩擦得到区域I处的切削分力为：

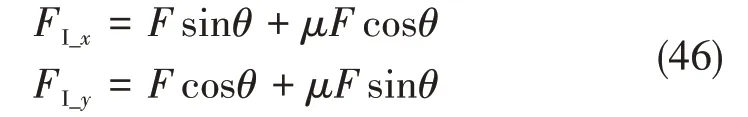
1.4.2 纤维树脂断裂区的切削分力

逆向切削过程中，区域Ⅱ受到弯曲载荷的作用，主要发生纤维和树脂的剥离及纤维与树脂的破碎，CFRP 单向板中纤维所受应力达到细观弯曲强度，RVE去除形成粉状切屑，其作用范围为：

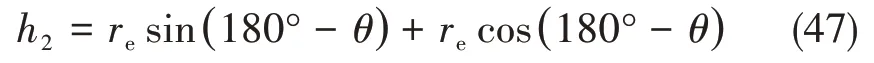
由式（2）和式（47）得到区域Ⅱ的切削分力为：

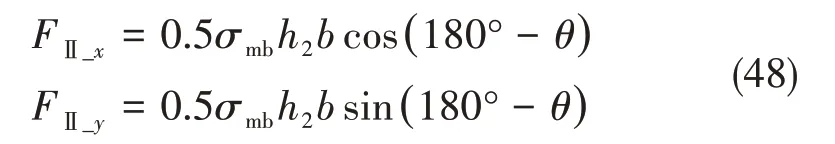
综上两区域切削分力叠加后可得：

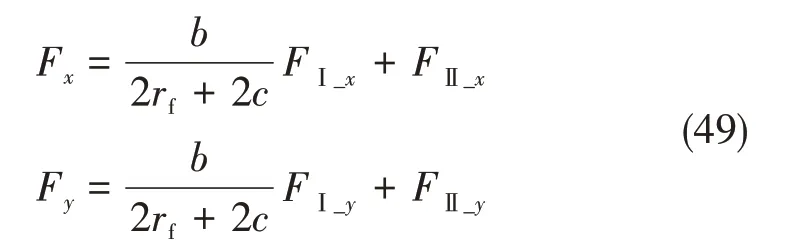
2 CFRP铣削加工实验

2.1 实验材料

CFRP 层合板为委托恒神股份有限公司生产的T700 型单向层合板，纤维方向为0°、45°、90°和135°四种，单层厚度为0.125 mm，板厚5 mm，共计40 层，工件长170 mm、宽120 mm，其中纤维体积分数为60%，纤维半径为3.5 μm，树脂及界面相厚度为0.5 μm，其质量密度为1.21 g/cm3，CFRP 及其组成成分的材料参数详见表1。

表1 T700型单向板材料参数Tab.1 Material parameters of T700 unidirectional plate

为与实际铣边加工过程相符，提高加工质量，实验采用专门定制的整体硬质合金直刃立铣刀对CFRP 单向板进行侧铣加工，其铣削过程便于观测，且直刃立铣刀铣削和直角切削也有相似性。

硬质合金铣刀的Et为700 GPa，νt为0.07，根据铣刀的设计数据可知其几何参数如表2所示。为确保切削刃的锐利程度，对CFRP进行高效切削，故未对刀具进行涂层处理。利用Alicona刃口半径测量仪，用垫板支架将铣刀测试刃口域工作台平行放置，通过直刃扫描模式获得如图9所示的刀具刃口半径为re=2.425 μm，刀具前角γ0=10.24°，刀具后角α0=9.62°。

表2 硬质合金铣刀几何参数Tab.2 Geometric parameters of carbide milling cutter

图9 硬质合金直刃立铣刀测量Fig.9 Measurement of carbide straight edge end milling

2.2 实验设计

为对CFRP切削力模型进行验证，进而研究其切削力变化规律，采用德玛吉五轴联动加工中心DMU80T对四种典型纤维方向角的CFRP单向板侧铣加工。待加工CFRP单向板利用上下两块压板压紧，以降低铣边加工过程中的振动对测量结果的影响，使用内六角圆柱头将其固定在Kistler9257B三通道测力仪上，测力仪下方与工作台完全固连，测力仪输出数据经过信号放大器及数据采集器处理后，传输到专用计算机处理。在实验过程中为降低CFRP切屑粉尘对人体的影响，实验时带上口罩并利用吸尘器同时对加工过程中的切屑进行收集，CFRP铣削加工设备及实验现场如图10所示。其中沿刀具进给方向为x向，垂直进给方向为y向，刀具轴向为z向。

图10 CFRP加工设备及实验现场Fig.10 CFRP milling processing equipment and test sites

硬质合金直刃铣刀在四种典型纤维方向角的CFRP单向板的长边方向逆铣进给，实验加工参数选用实际工程加工中的常用数值，如表3所示，每组实验进行三次以降低实验误差，同时记录实验结果进行后续分析。

表3 侧铣加工参数表Tab.3 Parameters of side milling

3 实验结果及对比验证

3.1 切削过程的转化

硬质合金直刃立铣刀的每齿进给量和刀具半径相比相差较大，从而刀齿的螺旋铣摆线轨迹可以等效为圆形轨迹。在铣削加工过程中，CFRP 单向板的切削厚度随着刀具旋转的变化而时刻产生改变。为进行切削力模型的验证，选用直刃铣刀将二维和三维铣削过程等效，逆铣加工时刀具切入切出的过程中，厚度由零增加到最大，如图11所示。

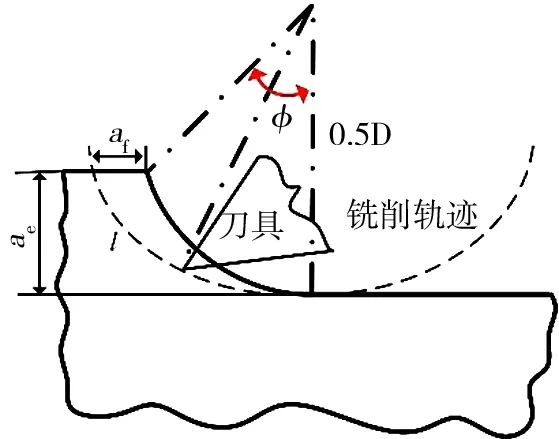
图11 铣削加工过程的等效Fig.11 The equivalence of milling process

由于刀具直径远大于铣削过程中的切削厚度，选用平均切削厚度aavg进行后续计算［18］：

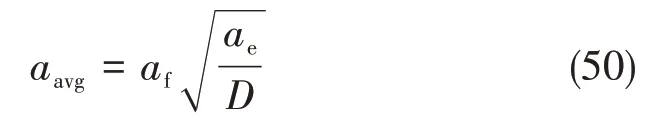
式中，af为每转进给量，逆铣加工时切削速度方向和纤维铺层方向相交沿顺时针旋转形成的夹角为纤维切削角β，和纤维方向角θ、刀齿旋转角φ的关系表达式：

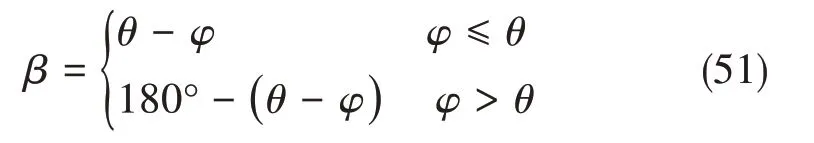
3.2 临界损伤长度L

作为典型硬脆材料的CFRP，纤维断裂与树脂破损采用最大应力准则。通过上文的切削力学分析，利用式（16）、式（33）和式（44），结合T700型单向板材料参数对不同纤维方向角的临界损伤长度迭代计算，其计算结果如图12所示。图中曲线为等间隔选取十二个不同纤维方向角迭代计算得到的临界损伤长度计算结果的拟合曲线。

当θ=0°时，刀尖和CFRP 单向板接触，产生沿纤维方向的裂纹及延展，先于铣刀对CFRP 的切削，形成“二次切削”的过程，故其临界损伤长度是一个较小值。当θ<30°时，临界损伤长度的增长趋势很平缓，而其在30°～180°时，临界损伤长度随着纤维方向角的增加先急剧增大而后又快速减小，在θ=120°附近达到最大值。

从CFRP 铣削区域随机取样，作去除表面毛刺处理后再进行喷金操作，采用QUANTA 250 FEG 环境场发射扫描电子显微镜对试件进行微观图像的采集与记录如图13～16所示。

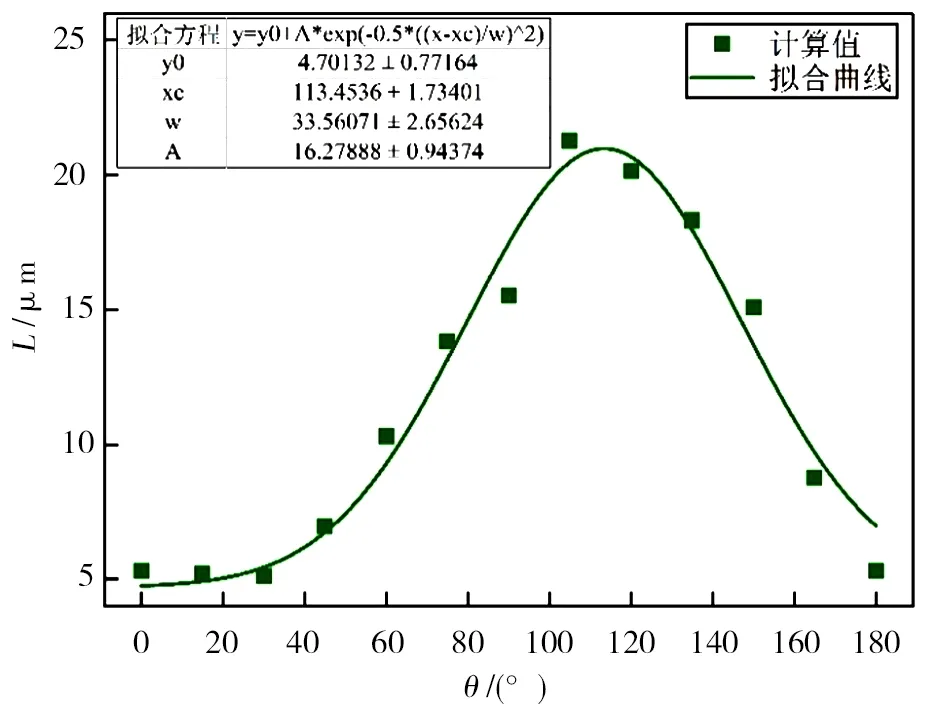
图12 临界损伤长度随纤维方向角的变化规律Fig.12 The change law of critical damage length with fiber orientation angle

图13 θ=0°时对应的加工表面Fig.13 Machining surface when θ=0°

图14 θ=45°时对应的加工表面Fig.14 Machining surface when θ=45°

图15 θ=90°时对应的加工表面Fig.15 Machining surface when θ=90°

图16 θ=135°时对应的加工表面Fig.16 Machining surface when θ=135°

从图13可知，当θ=0°时，加工表面平整，纤维和树脂界面表面形貌良好，纤维存在从树脂剥离的现象导致树脂的较小破损；对于θ=45°，由图14可以看出树脂涂覆现象出现在加工表面，部分纤维因刀具挤压而断裂且断裂长度较长；对图15可以明显观测到加工表面以下的纤维折断且尺寸较大，已加工表面的树脂剥离，凹坑数量较多，当θ=90°时，铣刀具对CFRP 产生较大损伤；当θ=135°时，从图16可看到明显裂纹，切削力对纤维弯曲作用导致纤维断裂长度较长，已加工表面极为不平整，加工质量极差。对加工表面观测，随着纤维方向角的增加，被切削纤维断裂时的变形长度先增后减。主因是当切削深度一定且θ<90°+γ时，纤维方向角增大则切削段上部分长度减小，即刀具与纤维自由段的距离减小，被切削纤维与刀刃接触点上方的纤维受到未加工侧材料的约束作用越弱而其下方区域所受约束作用未发生改变，因此随着纤维方向角的增大挤压切断难度增加，形成的损伤长度也在增加，θ>90°+γ则反之；当纤维方向角较小时，纤维断裂时的变形长度较小，可以得到好的加工表面质量。以上结果间接验证了临界损伤长度随着纤维方向角的变化趋势。

3.3 实验结果与对比验证

利用硬质合金直刃铣刀对CFRP 单向板逆铣加工，采样频率10 kHz时，获取三个方向四个切削刃的力的周期变化曲线。选取θ=0°，进给速度Vc=400 mm/min，变化曲线如图17所示。

从图中可以看出，单刃切削CFRP 过程中任意时刻法向力Fy均大于进给力Fx，轴向力Fz接近于零，这和直刃立铣刀加工时不产生轴向力的规律相符。x向和y向切削力信号存在波动且y向切削力波动幅值要大，这是因为θ=0°时对应的纤维切削角从180°变化到150°，其切削断裂也经历了劈裂和弯折断裂等过程。

在给定的进给速度下，用式（49）计算可得其等效平均切削厚度为6.32 μm 和12.64 μm，分别获取实验条件下四种单向板稳定切削区域切削力最大值的平均，则x、y和z向的切削力变化如图18所示。

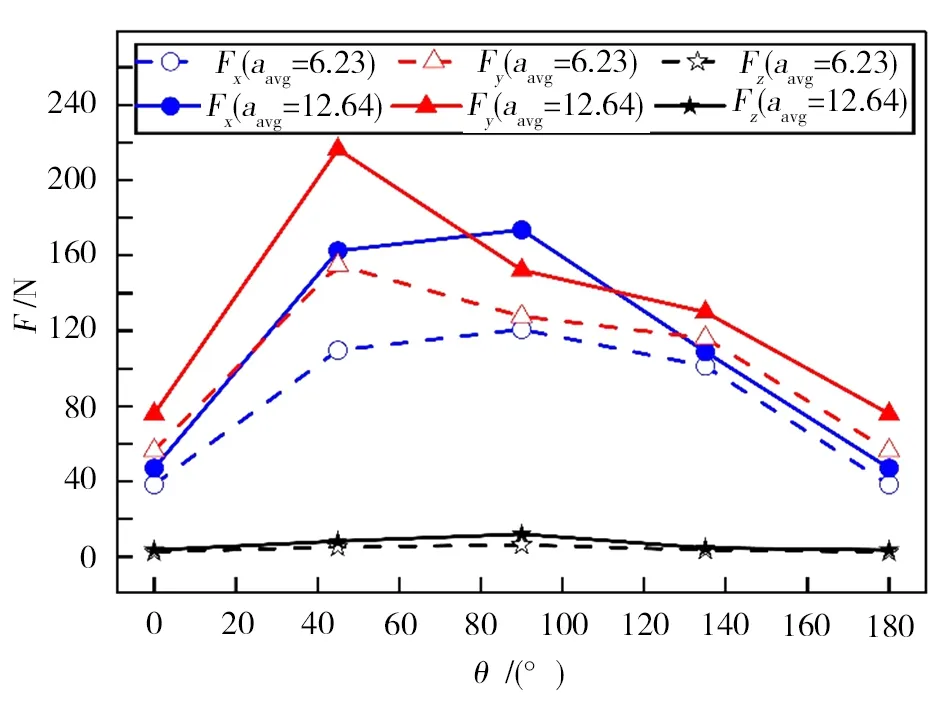
图18 aavg为6.32和12.64 μm时三向切削力对比Fig.18 Comparison of three direction cutting forces at aavg of 6.32 μm and 12.64 μm

进给力Fx小于法向力Fy，均随着纤维方向角的增加而先增大后减小，但进给力Fx在纤维方向角为90°附近达到最大，法向力Fy在纤维方向角为45°附近最大，并转变变化趋势。直刃立铣刀的z向（轴向力）力随纤维方向角的变化有增大但变化幅值不大。随着切削厚度的增大，各个方向的切削力均有增大，当纤维角度较小时尤为明显，因纤维方向角小时，刀具前刀面对切削力的影响较大，而切削厚度主要就是通过前刀面影响切削力。

在硬质合金直刃铣刀逆铣加工CFRP 单向板过程中，其纤维切削角β在不断变化，由式（50）计算可得，任一纤维方向角θ对应的纤维切削角β的变化范围，从而求得对应切削力的平均值作为宏观理论值。根据实验结果知轴向力极小，故将计算值和实验测得的切削力，分为沿着刀具进给方向的进给力和垂直刀具进给方向法向力进行对比，如图19示。

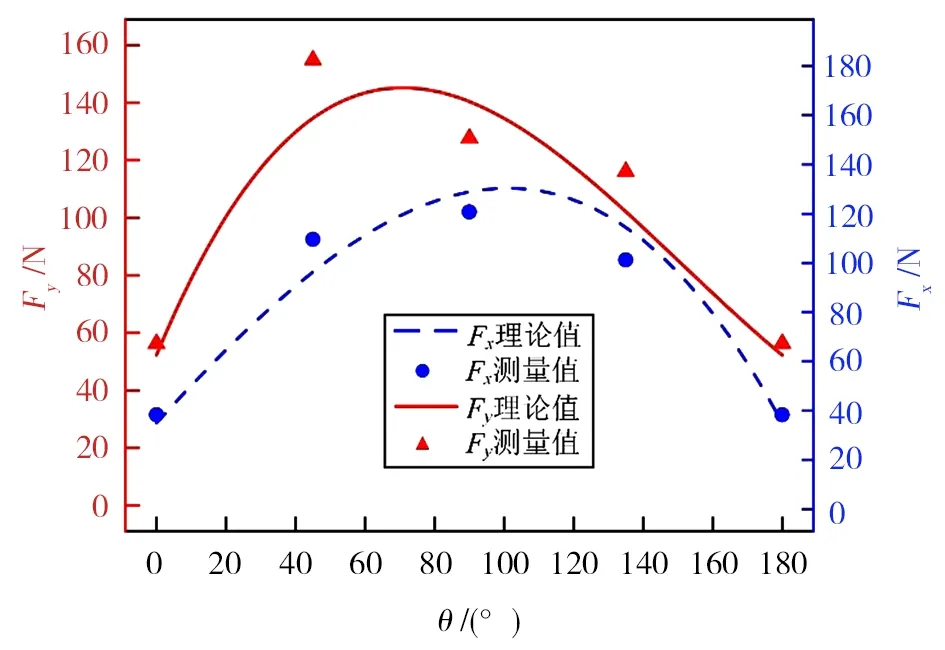
图19 aavg=6.32 μm时切削力理论值和测量值对比Fig.19 Comparison of theoretical value and experimental data of cutting force when aavg=6.32 μm

结果表明，进给力Fx和法向力Fy均在θ=45°和θ=90°理论值和测量值存在一定偏差，主要是纤维为直接切断型，周围材料产生的支撑作用影响切屑的正常脱离，故测量值对比实验值因外部因素产生偏差。在θ为0°～180°时，理论切削力的变化规律为先增大后减小，进给力Fx在90°附近转变，法向力Fy在45°附近转变，y向的切削力要比x向大。本模型在纤维方向角度全周期内对三个变形区域的受力都进行了一定的简化，另外宏细观切削力模型的基础是最小势能原理和Winkler 弹性地基梁理论，对二维RVE 分析，考虑到周围材料的约束作用，但切削宽度上的其他单元体约束缺少分析，从而导致在推导切削力上有所偏差。总体来看，本模型的宏观切削力计算结果相对误差在15%以内，其计算精度较高，切削力分析计算的准确性也得到验证。

4 结论

从力学建模的角度对CFRP 切削行为进行研究，对RVE所受树脂及界面相的粘结作用和周围支撑材料的约束作用加以考虑，探讨了临界损伤长度和切削力受纤维方向角的影响，实现了动态切削过程中的切削力学模型的建立。最后通过实验结果验证了切削力学模型的正确性，得出以下主要结论：

（1）临界损伤长度在纤维方向角为0°时因存在“二次切削”而取得极小值，当小于30°时增长较慢，在30°～180°间先快速增大后急剧减小。

（2）对比计算值与实验测量值的变化趋势一致，进给力Fx和法向力Fy均随纤维方向角的增大先增后减，进给力Fx小于法向力Fy且分别在90°、45°附近转变。

（3）基于最小势能原理和Winkler 弹性地基梁理论求解的切削力与实验结果对比，相对误差在15%内，验证了本文CFRP切削力学模型的正确性。