两自由度并联机构性能指标分析
王学雷,张 宾,吕世霞,王 京
(1.北京电子科技职业学院,北京 100176;2.中国农业大学,北京 100083)
1 引言
并联机构具有刚度大、误差小、结构紧凑、承载能力大、动态响应性能好等优点而受到人们的青睐[1-3]。与6 自由度并联机构相比,少自由度并联机构具有成本低、结构简单、控制容易等优点而成为国内外学者的研究焦点[4-6]。
机器人运动学性能好坏直接影响其运动效果,如何评价运动学性能好坏是机器人研究的重要内容之一。为了评价机器人运动学性能好坏,研究者提出多种运动学性能评价指标,为机器人的优化设计提供了依据[7-9],但这些指标仍存在评价不全面、不系统等问题。利用各向同性指标对2UPS+U 并联机构进行性能指标分析,并根据统计学中的变异系数,提出了机构全域性能波动指标公式,得到机构尺寸与性能波动指标之间的关系图谱,为机构的优化设计提供了理论依据,避免了尺寸选取的盲目性。
2 两自由度并联机构速度同性指标分析
所述的两自由度并联机构由机座、两个结构完全相同的SPU(球副-移动副-虎克铰)型驱动分支以及一个U(虎克铰)型约束分支构成,可等效为2SPU+U 并联机构,如图1 所示。参考文献[10]对该机构及其用途进行了详细介绍。
设并联机构输出速度和输入速度映射关系,如式(1)所示。

式中:Vc—输出速度;v—输出线速度;ω—输出角速度—并联机构各关节输入速度;J∈6×n—并联机构速度雅可比矩阵。
将机器人线速度和角速度分开单独进行分析。定义并联机构速度雅可比矩阵为 J=[JνJω]T,其中,Jν∈R3×n为机构线速度雅可比矩阵,Jω∈R3×n为机构角速度雅可比矩阵,则式(1)可写为如下表达式:

根据范数概念,对式(2)两端同时取2 范数,得:

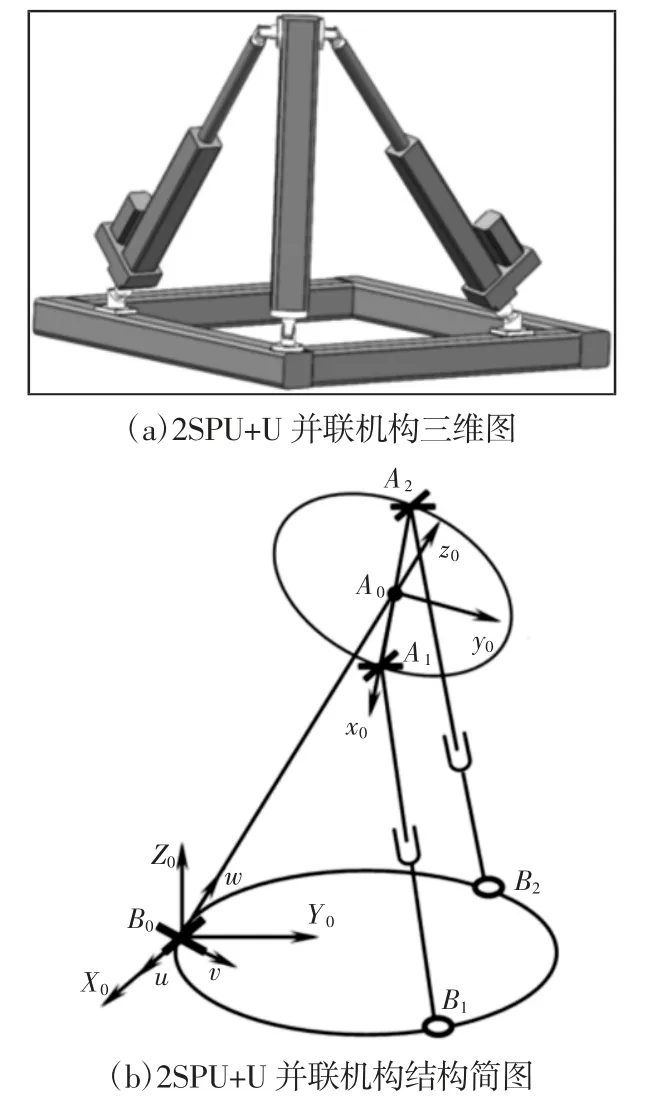
图1 2SPU+U 并联机构Fig.1 2SPU+U Parallel Mechanism
引入格朗日算子λν、λω,结合式(2)和式(3)可构造如下方程式:

设机构输入速度为单位速度向量,即:

对式(4)求偏导,并结合式(5)可得机构输出线速度和角速度极值条件为:
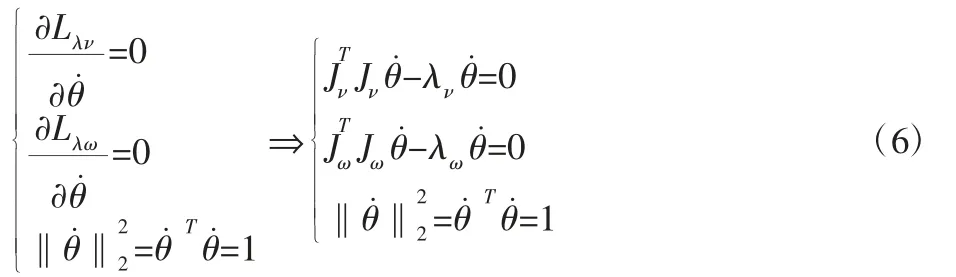
式中:λν—矩阵的特征值;λω—矩阵的特征值,即式(6)取得极值条件为 λν和 λω分别取矩阵和的特征值。将式(6)求得的特征值 λν和 λω分别代入式(3)可得机构输出线速度和输出角速度极值[11],即:

在机器人工作空间内,线速度和角速度向量分别构成一个n维椭球体,研究者基于椭球短轴和长轴的比值介绍了一种速度各向同性评价指标,如式(8)所示。

该指标描述速度椭球的扁率,K 越大,速度各向同性越好。
两自由度并联机构有两个速度输入,因此线速度和角速度雅可比矩阵各有两个奇异值,基于式(8)定义该两自由度并联机构线速度和角速度各向同性指标,如式(9)所示。

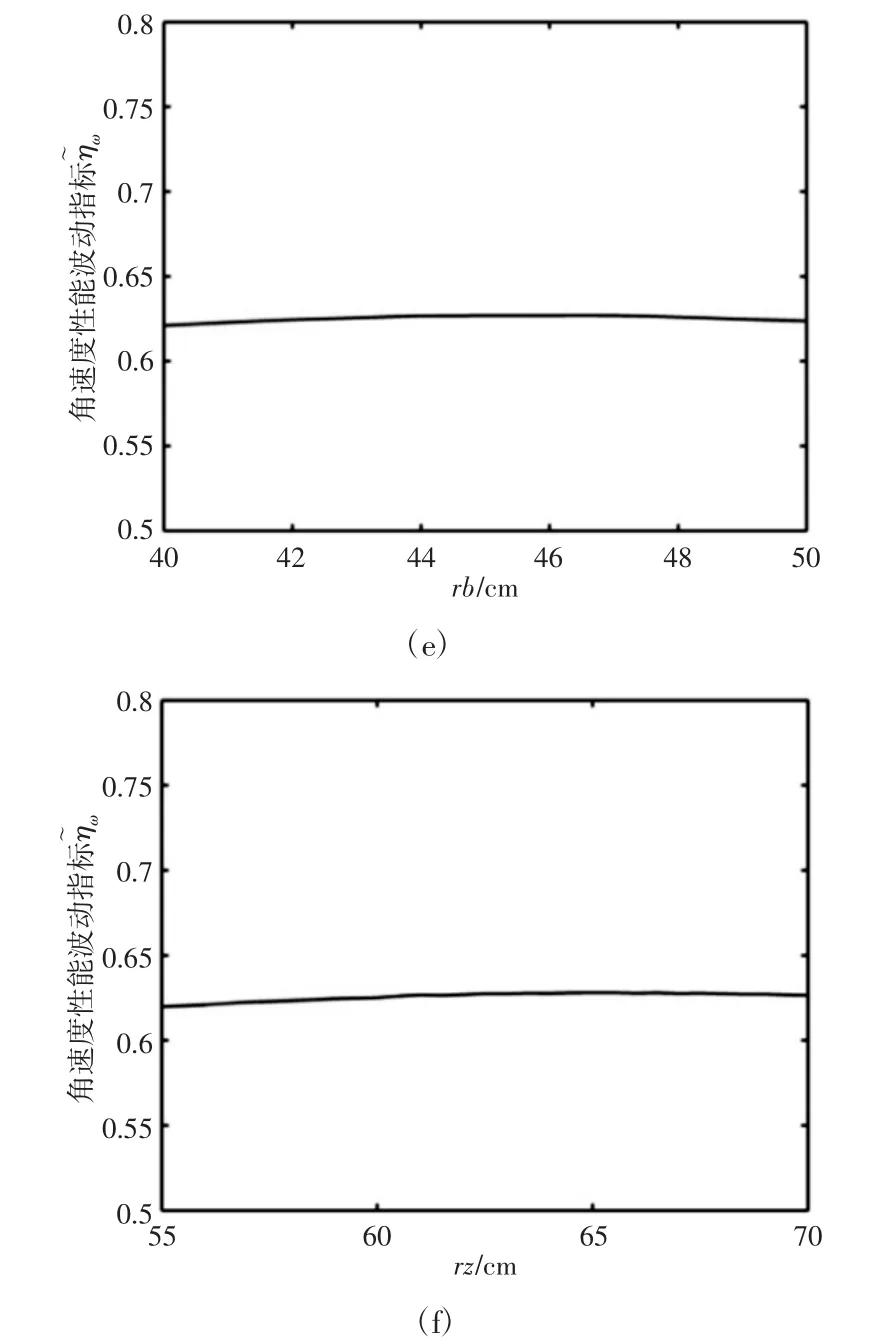
式中:σνmax—矩阵 Jν的最大奇异值;σνmin—矩阵 Jν的最小奇异值;σωmax—矩阵 Jω的最大奇异值;σωmin—矩阵 Jω的最小奇异值,0 根据参考文献[10]运动学部分预选机构参数,借助Matlab 软件对两自由度并联机构线速度和角速度各向同性指标进行拟合,得到Ktv和Ktω在工作空间的分布图,如图2 所示。 图2 Ktv 和 Ktω 的分布图Fig.2 Ktv and Ktω Distribution Diagram 从图2 可以看出,角速度各向同性指标较大,线速度各向同性指标较小,说明工作空间内角速度各向同性较好,线速度各向同性较差,且线速度和角速度各向同性指标均对称分布于X=0轴线上,在X=0 轴线上线速度性能较差,而在X=0 轴线两侧随着与X=0 轴线的远离,线速度性能指标越来越好,在X=(-21~-17.5)cm,Y=(40.5~46.5)cm 和 X=(17.5~21)cm,Y=(40.5~46.5)cm时,线速度性能指标最好,其最大值为Ktv=0.011453;而角速度性能指标在X=0 轴线上性能最好,而在X=0 轴线两侧随着与X=0轴线的远离,角性能指标越来越差,在 X=(-3.3~3.3)cm,Y=(0~25.5)cm 时,角速度性能指标最好,其最大值为 Ktω=0.59033。通过以上分析可知线速度同性指标与角速度同性指标具有矛盾性。为了全面评价机器人在整个工作空间线速度和角速度传递性能,定义线速度和角速度全域各向同性指标如下: 式中:0<ηKtv<1,0<ηKtω<1,W—机构可达工作空间。 由式(10)可知,机构线速度和角速度全域各向同性指标越趋近于1,机构在工作空间线速度和角速度传递性能越好。 速度全域同性指标ηKtv和ηKtω只反映机构线速度和角速度各向同性的均值,并不能反应整个工作空间内各向同性波动幅度大小,因此,基于统计学中变异系数概念提出一种机构全域性能波动指标作为上述全域同性指标的辅助性能评价指标,设η¯J为性能指标ηJ的标准差,即: 则机构全域性能波动指标公式可表示为: 采用单变量分析法,逐个分析重要结构参数(ra rb rz)对性能波动指标的影响规律,借助Matlab 软件分别绘制关键尺寸(ra rb rz)对性能波动指标的影响曲线,如图3 所示。其中,仅考虑ra、rb、rz 变化时对线速度性能波动指标的影响关系,如图3(a)、图3(b)、图3(c)所示。仅考虑 ra、rb、rz 变化时对角速度性能波动指标的影响关系,如图3(d)、图3(e)、图3(f)所示。 图3 结构参数与和的关系Fig.3 Relationship Between and and Structural Parameters (1)在两自由度并联机构2SPU+U 工作空间内,角速度各向同性指标较大,线速度各向同性指标较小,线速度同性指标与角速度同性指标具有矛盾性。 (2)针对速度全域性能指标的不足提出全域性能波动指标公式,采用单变量分析法,逐个分析了重要结构参数ra、rb、rz 对性能波动指标影响规律,通过分析可知ra 的增大会使整个并联机构运动线速度和角速度波动程度增大,不利于机构的平稳运行;rb 的增大会使机构线速度运动波动程度增大,rb 的增大对角速度波动性能影响较小。rz 的增大有利于线速度和角速度性能波动的减小,有利于机构的运动控制。 (3)通过机构全域性能指标和全域性能波动指标图谱,得到尺寸变化对机构性能的影响趋势,为机构的尺寸选取以及优化设计提供理论依据,对机器人重要结构尺寸的选取以及控制方案的设计有着重要意义。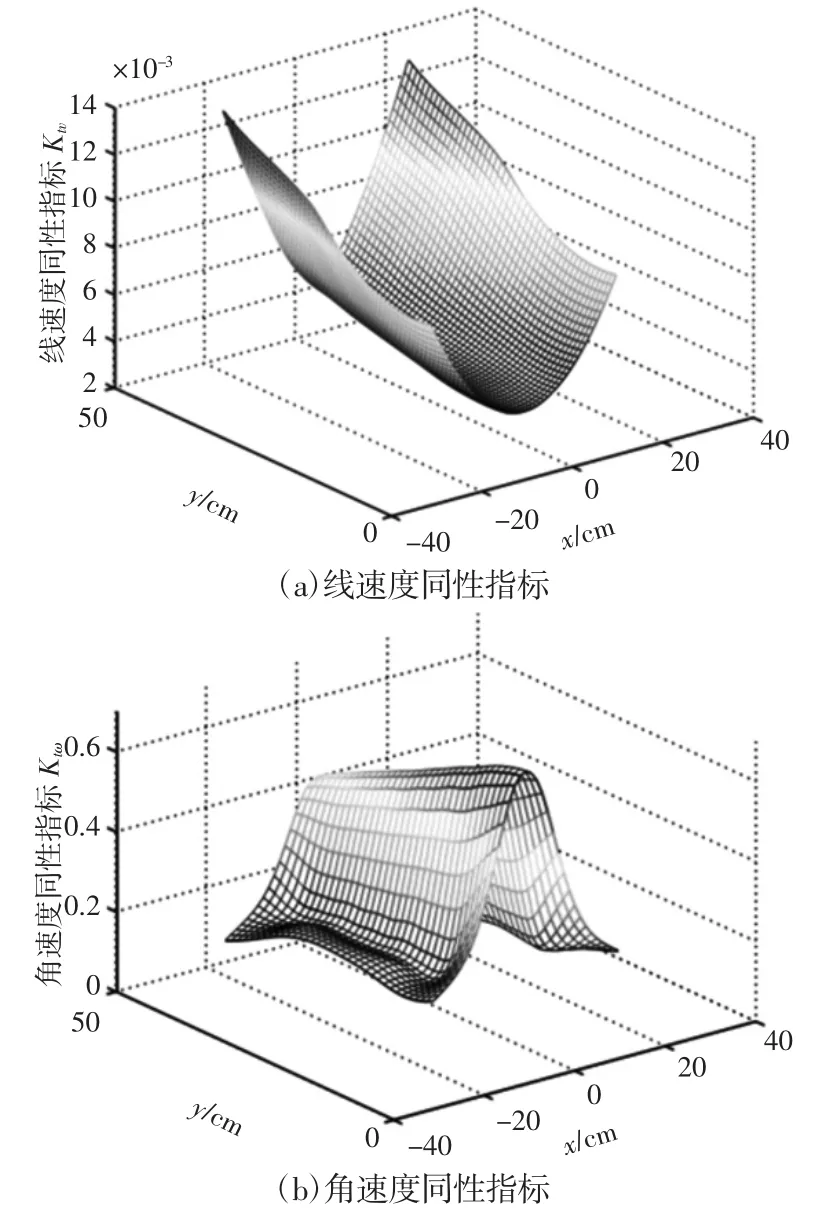

3 两自由度并联机构全域性能波动指标分析
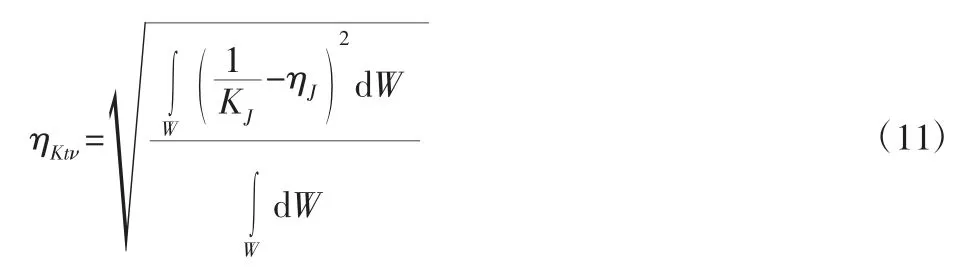
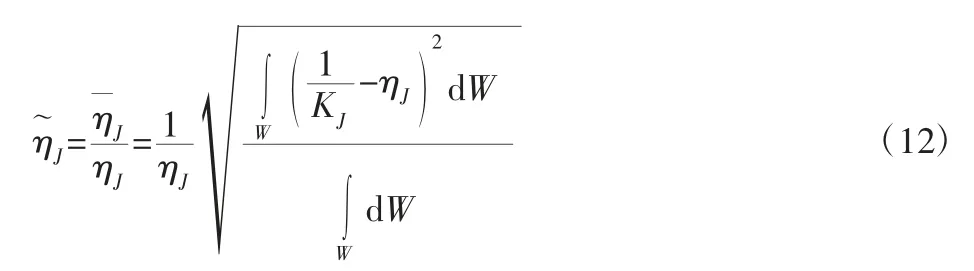


4 结论

