拉杆转子轮盘结合面切向接触刚度试验研究
吕超颖,张锁怀,李俊南,纪林章
(上海应用技术大学机械工程学院,上海 201418)
1 引言
分布式拉杆转子具有诸多优势,如重量大、刚度大、易于拆卸组装等,但是,由于存在接触面,在很大程度上,破坏了拉杆转子的连续性[1],所以,重点研究结合面的接触特性显得甚是紧要[2-3],为后来的研究者提供参考。结合面存在着接触刚度,而且粗糙表面形貌对结合面接触刚度产生重要影响[4-5]。所以,研究者们开展了大量的研究表面形貌的理论工作。首先,从统计分析平面的GW 模型被美国康涅狄格的Greenwood 和Williamson 提出以后,接着,M-B 接触模型[6]被提出,它是由Majumdai 和Bhushan 在研究过程中得出的,具体地讲,机械加工表面具有自仿射分形特征,粗糙表面的表征参数(分形维数D 和特征长度尺度参数G)具有尺度独立性,不受仪器分辨率的影响。结合这一接触分形理论,文献[7-9]也研究了结合面接触刚度,分别提出了结合面的切向接触刚度的分形模型。以上这些模型始终是从理论分析入手,对理论模型的精度和使用范围没有进行验证。
就上述理论工作的不足之处,拉杆转子轮盘结合面间的接触效应着重从试验方面开展。同时,结合轮盘表面微观形貌的特征分析,基于文献[10-11]中计算分形参数的方法,建立起理论模型,进行仿真分析与计算,并运用试验手段,对比分析拉杆转子轮盘结合面切向接触刚度的相关问题。着重接触静刚度的试验研究,不具备动刚度研究的条件。
2 分形参数与轮盘粗糙度的关系
2.1 分形参数计算方法
运用分形接触理论,可理论模拟出粗糙表面的实际轮廓曲线,用处处连续、点点不可微、统计学自相似性的Weierstrass-Mandelbrot 函数[12]来逼近。分形维数D 与分形粗糙度参数G 可通过对功率谱密度函数(power spectral density,以下简称 PSD)P(ω)做导数得到。


式中:γ—仿形参数,机械加工表面一般取γ=1.5;ω—空间频率,单位是m-1。
对式(1)两边取对数,得:
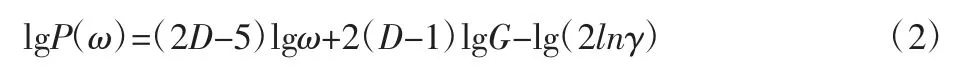
令 2D-5=k,b=-2(D-1)lgG-lg(2lnγ)
式(2)可以写成:

从式(3)可以看出,PSD 在对数计算后的平面坐标系上并非曲线,而是一条直线,k、b 分别表示双对数坐标方程 lgP(ω)-lgω的倾斜度、与Y 轴交点的纵坐标,如图1 所示。

图1 实测、拟合PSD 曲线Fig.1 Measured,Fitted Power Spectral Curve
根据其关系式可得:

由k 和b,就可以计算出分形参数(一定条件下。表现为与整体的相似性)D 和G。
2.2 分形参数的试验方案
设计、加工八组试验轮盘,每组五个,直径140mm,厚度37mm。45 号钢,经过调质处理,HB220~250。轮盘接触表面采用车削方式进行加工,而且表面粗糙度Ra的设计值分别为:0.4、0.8、1.6、3.2、6.3、12.5、25 和 50。采用英国某公司制造的 Talysurf CCILite 超精密三维形貌测量仪测量轮盘表面粗糙度,如图2 所示。在每个试验轮盘的上下端面上取8 个沿圆周方向均匀分布、长20mm 的测量长度,测量长度沿半径方向。在轮盘粗糙度测量过程中,发现其中一组轮盘的粗糙度值非常分散,而且与设计值相差较大,因此,剔除了该组轮盘数据,在后文的轮盘刚度试验中,也没有考虑该组轮盘,其余轮盘粗糙度试验数据,如表1 所示。
在第一组、第二组轮盘中,其中各有一个轮盘的粗糙度值出现较大偏离,在刚度试验中,没有使用。因此,在表1 中,没有给出。
对实测表面粗糙度Ra数据进行功率谱分析之后,将分析结果转化到lgP(ω)-lgω 坐标系上。按前文中的算法,计算表面轮廓曲线的功率谱函数,并绘制实测曲线,再将实测值拟合为功率谱函数曲线,如图1 所示。
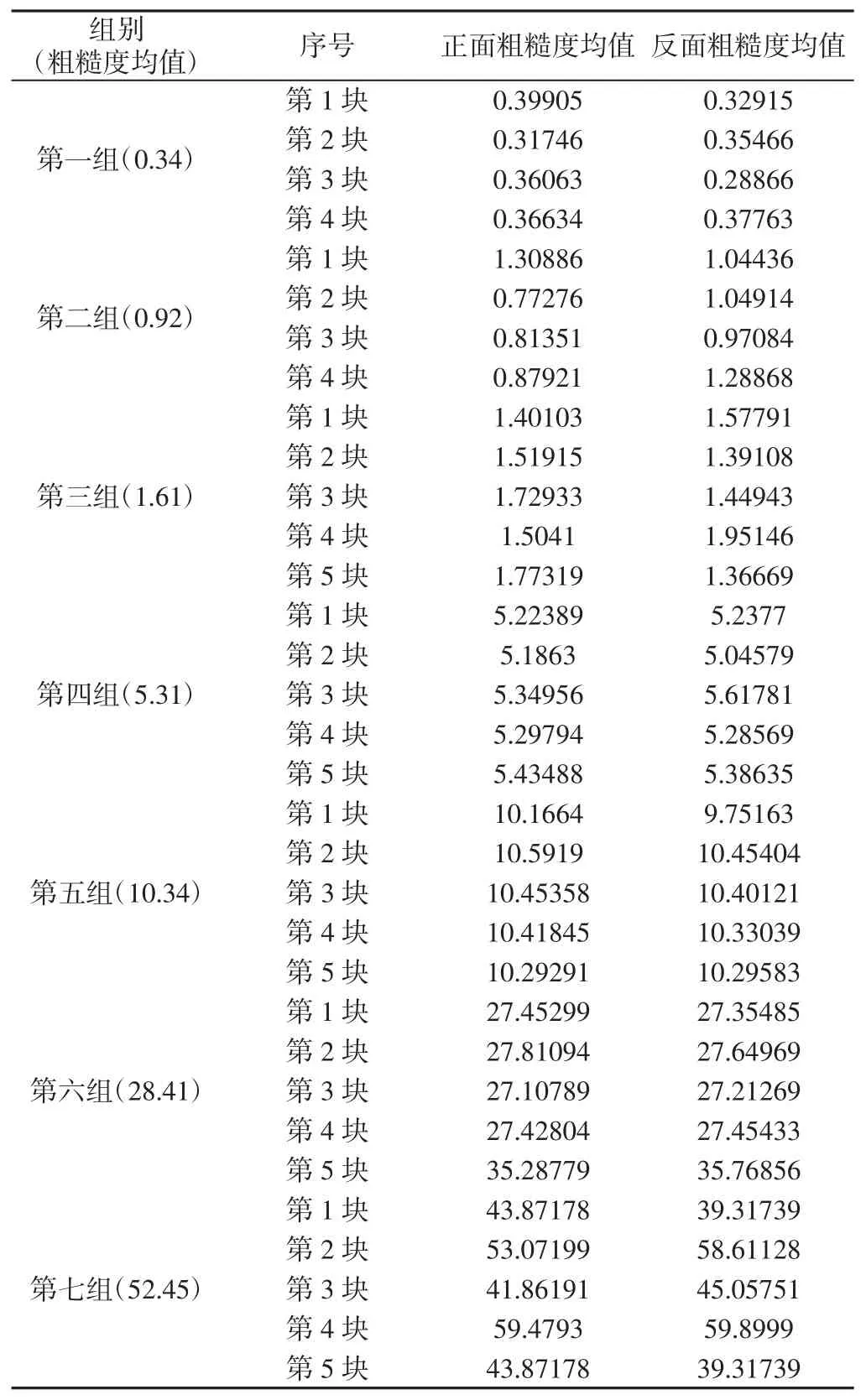
表1 轮盘粗糙度试验数据Tab.1 Roulette Roughness Test Data

图2 三维形貌测量仪测量轮盘RaFig.2 Three-Dimensional Topography Measuring Wheel Roughness

图3 分形维数-表面粗糙度关系Fig.3 Fractal Dimension-Surface Roughness Relationship

图4 分形粗糙度参数的指数-表面粗糙度的关系Fig.4 The Relationship Between the Index of Fractal Roughness Parameters and Surface Roughness
由于上述每一组试验数据呈现在平面上是一系列分散的点,需用光滑的曲线拟合连接起来,通过拟合直线的斜率和截距,可得D 与Ra之间的关系。再将每组表面粗糙度对应的分形维数、分形粗糙度参数绘制在二维图上,得到一系列离散点,如图3、图4 所示。
对这些离散点,用幂函数进行近似拟合,可得分形维数与表面粗糙度之间的近似换算式(其中,Ra的单位是μm)为:

对试验数据进行拟合,可得分形粗糙度参数与表面粗糙度之间的近似换算式(为了表达方便,令g=-logG)为:

3 切向接触刚度分形模型及仿真
3.1 切向接触刚度
基于文献[13]中的分形接触理论,结合面切向接触刚度可以由下式来计算:
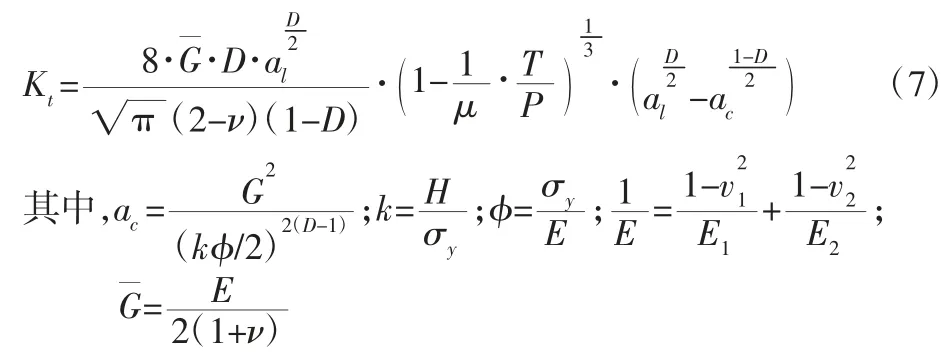
式中:al—最大的接触点面积;ac—临界接触面积;H—较软材料的硬度;σy—较软材料的屈服强度;E—两接触材料的复合弹性模量;P—结合面上的法线方向上的力;T—结合面上的切向载荷;和μ—结合面两接触材料的当量剪切弹性模量和摩擦系数;E1、E2和 ν1、ν2—两个接触材料的弹性模量和泊松比。
由式(7)可见,切向接触刚度Kt不仅与轮盘表面材料性能参数有关,还与作用在结合面上的拉杆转子法向力P、切向力T 和接触区域面积有关。同时需要指出:仅当T/P<μ 时,切向接触刚度Kt才存在;当T/P≥μ 时,转子轮盘将会发生相对滑动。
粗糙表面上的法向力P 可以表示为[13]:
当 1<D<2,D≠1.5 时,接触载荷为:
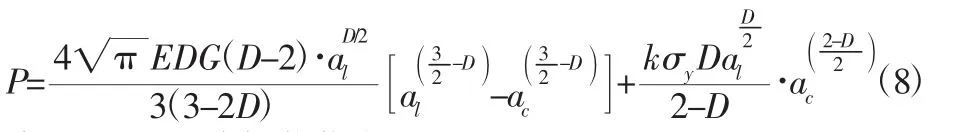
当D=1.5 时,接触载荷为:
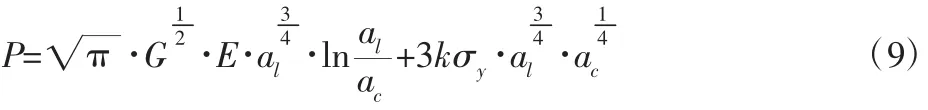
这样,由式(7)~式(9)可知,在结合面的切线方向上的接触刚度Kt与以下几大参数存在复杂非线性关系。分别为:作用在结合面上的法线方向上的力P、切线方向上的力T、粗糙表面材料性能参数(如表面硬度H、σy、E、当量剪切弹性模量G¯等)以及分形维数D、分形粗糙度参数G,由此构成了结合面切向接触刚度的分形模型。给定切向力T 和最大的接触点面积al,就可以通过式(7)~式(9)分别算出切向接触刚度和拉杆转子法向载荷,进而建立起切向接触刚度与切向载荷、拉杆转子法向载荷的关系。
根据临界接触面积ac的计算公式,当表面粗糙度确定时,临界接触面积也是定值;综合式(7)~式(8)可知,当拉杆转子法向力P 较小时,最大的接触点面积 al小于 ac,则 Kt为负;同样,当 Ra较大时,al变小,ac变大,也会造成切向接触刚度为负的情况。由此可说明,接触分形理论只适用于Ra较小、拉杆转子法向力P 较大的情况。
汾渭平原作为中国第四大平原,是全国空气污染最严重区域之一,2018年被生态环境保部纳入了“蓝天保卫战”治理重点区域。目前有关将汾渭平原大气污染作为一个整体进行卫星监测的研究报道较少。本研究将利用 OMI数据,综合运用空间插值、相关分析等方法对汾渭平原SO2季节性空间分布特征、逐月变化,以及不同时期平均年总量变化情况进行探讨,旨在全面认识汾渭平原大气污染现状,为本区域联防联控提供科学依据。
3.2 仿真与分析
轮盘材料性能及参数,如表2 所示。

表2 轮盘表面材料性能及参数Tab.2 Roulette Surface Material Properties and Parameters
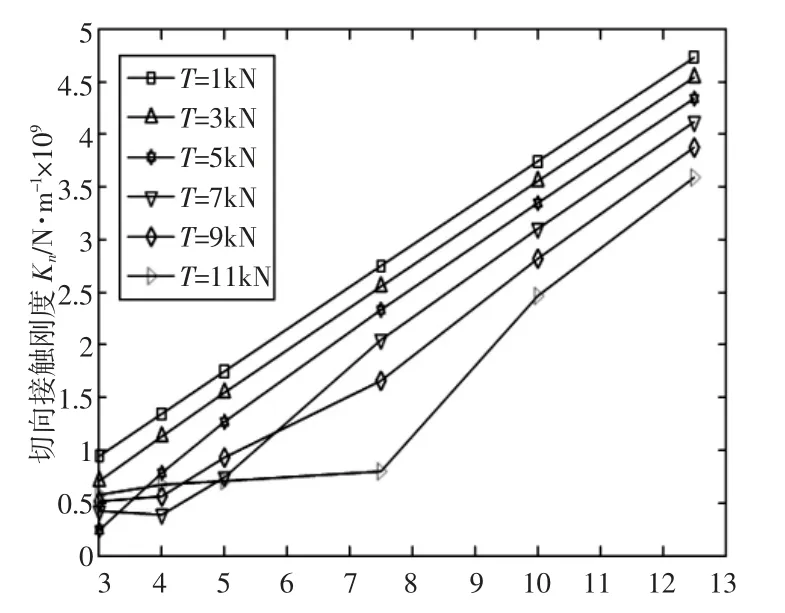
图5 粗糙度为0.34μm、不同切向载荷时,切向接触刚度随法向载荷变化的曲线图Fig.5 Roughness of 0.34,Different Tangential Load,the Tangential Contact Stiffness Curve With the Normal Load Changes
由式(7)可知,切向Kt与拉杆转子法向力P、切向力T 和轮盘Ra有关,为了比较Ra和P 对刚度Kt理论计算值和试验测量值的影响,考虑到分形接触理论仅适用于Ra很小、较大拉杆转子法向力的局限性,考虑到轮盘之间存在切向滑移和实际拉杆的抗破坏最大应力,在此处只选取表面粗糙度为0.34μm、0.92μm,法向载荷依次为 30kN、40kN、50kN、75kN、100kN、125kN,切向力依次为 1kN、3kN、5kN、7kN、9kN、11kN。计算结果,如图5、图6 所示。由于粗糙度为0.92 时,拉杆转子法向载荷小于50kN 的切向接触刚度理论计算值为负,所以,图6 的计算结果中,粗糙度为0.92时,最小拉杆转子法向载荷为50kN。
由图5、图6 可知:拉杆转子结合面的刚度Kt随法向力的增大而增大,这是因为随着拉杆转子法向力增大,结合面的受剪面积也将增大,从而其Kt增大;拉杆转子结合面的随着结合面Kt间的切向力T 与法向力P 之比的增大而减小,即在结合面法向载荷一定的情况下,结合面Kt随着结合面间切向载荷T 的增大而减小。
在图5 中,当切向载荷逐渐增大为11kN 时,拉杆转子轮盘之间出现滑移,导致切向接触刚度值增加趋势与较小切向载荷的切向刚度值的增加趋势不太一致。
4 切向接触刚度的试验研究
4.1 试验装置及过程
轮盘结合面切向刚度试验装置,包括万能试验机、拉杆转子(通过拉杆将各轮盘压紧组装在一起,拉杆有八根,分布在轮盘周向某一半径处)、校正套筒(尺寸、结构与五个叠加轮盘相同,唯一区别是没有接触面,为整体结构)和两个数显千分表,如图7 所示。

图7 轮盘切向接触刚度试验装置Fig.7 Wheel Tangential Contact Stiffness Test Device
万能试验机架的顶部设有上压头,数显千分表一和数显千分表二位于上压头的两侧、第2 和第4 块轮盘外圆面上,机架的中部设有可移动的横梁,横梁上间隔设置两V 型块,将拉杆转子水平搭设在两V 型块上,且位于所述上压头的正下方,如图7 所示。万能试验机对拉杆转子或校正套筒加压,直至轮盘间出现滑移。记下两个数显千分表的读数。典型的加载曲线,如图8 所示。每条曲线代表一次加载过程。纵坐标表示对拉杆切向加载时,经数显千分表一测得的轮盘位移a1。
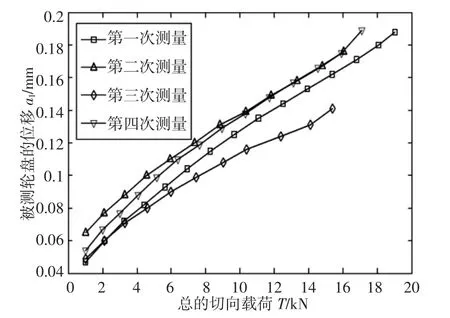
图8 结合面切向变形量与压头作用力关系图Fig.8 The Relationship between the Tangential Deformation of the Joint Surface and the Pressure Head Force
4.2 数据处理
对拉杆转子切向加载时,经两个数显千分表测得的轮盘位移为 a1、a2;
将轮盘组拆卸下,对校正套筒切向加载时,经两个数显千分表测得的校正套筒切向位移为b1、b2。
需要说明的是,对校正套筒加压时,是为了排除轮盘自身形变、工作台变形、轮盘外圆面与V 型块的接触变形、V 型块与工作台的接触变形、压力机传力系统变形等因素所带来的影响。
(1)计算拉杆转子之间结合面的切向变形量:

则一个结合面的切向变形量δ,关系式如下:

(2)绘制接触面上的切向载荷与结合面的切向变形量关系图,如图9 所示。利用最小二乘法拟合出其幂关系式。根据拉杆转子轮盘之间的切向变形量随着法向载荷增大而变小的原则,选取符合该趋势的相关数据作为计算数据。这里只给出粗糙度为0.34μm 不同法向载荷的幂关系式。
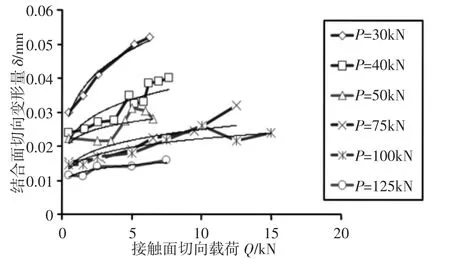
图9 切向载荷与结合面切向变形量关系图Fig.9 The Relationship of Tangential Load and the Joint Interfaces Tangential Deformation


然后对这些幂关系式求导,即可得到结合面切向接触刚度Kt。

4.3 试验刚度结果与理论模型对比分析
对于本次试验的结合面,切向接触刚度随接触面上的切向载荷的变化不是太大,暂且不分析轮盘结合面切向接触刚度随切向载荷的关系。
粗糙度为0.34μm、0.92μm 时,理论模型和试验获得的结合面切向接触刚度随拉杆转子法向载荷的变化规律,如图10、图11 所示。
由于切向载荷不止加一次,所以图10、图11 只给出切向总载荷为10kN 时的切向刚度,图中的试验切向刚度与理论模型刚度趋势一致,但存在一定的误差。
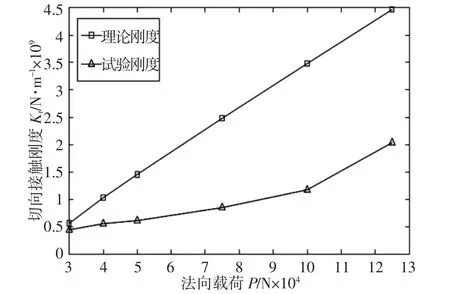
图10 Ra=0.34μm,理论与试验刚度随拉杆转子法向载荷变化关系图Fig.10 Ra=0.34μm,Theoretical and Experimental Stiffness with the Rod Fastening Rotor Normal Load Changes
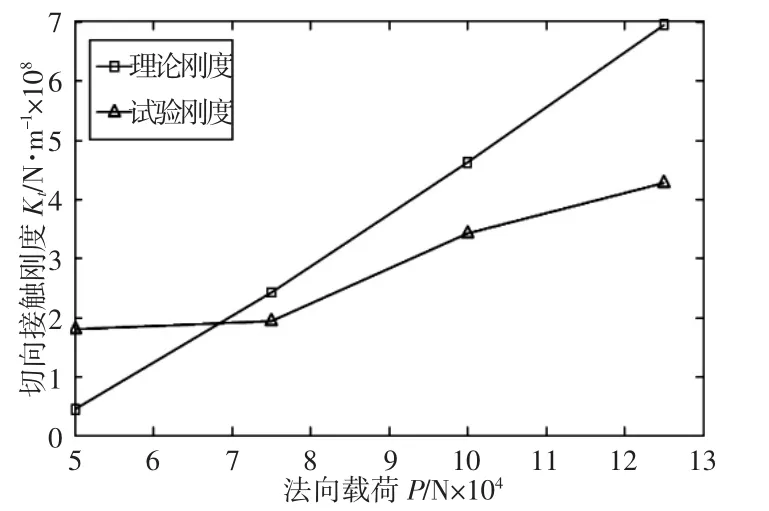
图11 Ra=0.92μm,理论与试验刚度随拉杆转子法向载荷变化关系图Fig.11 Ra=0.92μm,Theoretical and Experimental Stiffness with the Rod Fastening Rotor Normal Load Changes
由理论刚度与试验刚度结果可知:当表面粗糙度一定、拉杆转子法向载荷增大时,理论刚度和试验刚度都变大。由于轮盘结合面Kt是作用在结合面上的拉杆转子法向载荷的函数,所以增加结合面间的拉杆转子法向力,可提高轮盘Kt;理论Kt和试验Kt随着Ra 增大而减小,由于Ra 增大时,轮盘结合面最大接触面积减小,以至于Kt降低。
5 结论
(1)分形接触理论可以用于研究粗糙接触表面的切向接触刚度问题,但是,使用范围有限,与试验数据存在一定误差。
(2)有效提高轮盘切向刚度的方法是增加结合面间的拉杆转子法向力。
(3)表面粗糙度增大,则切向接触刚度随之减小。
(4)以上结论均为静刚度的范畴,下一步将准备动刚度的相关试验研究。

