《数学史》课程教学评价实践探索
徐传胜 杜彦武 谷龙飞 王富磊
(临沂大学 山东 临沂 276000)
数学教育家史密斯(D. E. Smith,1860—1944)在德国海德堡第三届国际数学家大会上,建议在大学设置精密科学史课程(含数学史),指明“数学史已被公认为是师范教育以及大中学校学生博雅教育中的重要学科之一。”[1]至1980年代末,美国有60%以上的师范院校开设《数学史》课程[2],至今达到了96%左右。
我国南开大学是国内最早设置《数学史》课程的高校,数学史家钱宝琮(1892—1974)于1925年始在该校讲授《数学史》;后在任浙江大学数学系主任期间,他亦为该系学生讲授《数学史》课程。自1980年始,我国师范院校及部分综合性大学陆续开设了《数学史》课程。随着科学技术的发展和进步,国内愈来愈多高校认识到学习数学史的重要性和必要性。据不完全统计,截至2019年,国内1246所高校(不含高职)中设置《数学史》课程者有776所,约占62.28%。其中既有清华大学、北京大学、南开大学等著名高校,也有临沂大学、鲁东大学、重庆文理学院等地方院校。
《数学史》是面向数学与应用数学专业本科生开设的专业选修课,每周2学时,记2学分。主要讲授古代数学(古埃及、美索不达米亚、中国、古希腊)、近代数学(中国、印度、阿拉伯、欧洲)和20世纪数学概观,并适当穿插介绍数学最新发展动态。侧重介绍数学概念、数学方法和数学思想的起源与发展,及其与社会、政治、经济和一般文化的联系。因数学史内容博大精深,故面对教学内容多、课时较少的矛盾,亟需在数学思想启迪与教学评价形式上有所创新。据多年教学经验,试对《数学史》课程进行了一些教学改革,尤其是在教学评价体系方面做了一些理论和实践探索。
一、《数学史》课程教学目标
数学教育的首要任务就是使人变得更聪明,让学生感悟到数学学习的乐趣和意义,实现自由全面可持续发展。任何一门数学课程都应教会学生“数学思考”,数学史更有着其独特的教育意义。有鉴于此,《数学史》课程应侧重于数学思想探讨,其主要教学方法为:
(一)思想引领:彰显着中国古典数学的辉煌成就,增强学生民族文化自信,激发其爱国情怀;分析数学科学演进规律,理解和把握数学发展的理论趋势;
(二)方法示例:分析数学史研究的典型方法,如“文献认证”“古算复原”“算理分析”“交流与比较”,以探索数学研究的内在规律性;
(三)案例分析:选择有代表性的经典论文开展探究性阅读和批判性思考,从中领悟数学研究的思想灵魂,进而培养“原创性研究”能力;
(四)文理融合:注重多学科交叉融合,引导学生不但从数学科学角度,亦要从历史、文化、艺术等视角认识问题、发现问题和解决问题。
从而体现出数学科学蕴含着丰富的人文精神,利用数学家的伟大成就,可培养学生爱科学、爱祖国情怀;重现数学家的创新思想,可激发学生的创新火花;挖掘数学家身上具有的辩证唯物主义因素,可帮助学生树立正确的人生观、世界观和价值观;弘扬数学家的高贵品质,可培养学生坚忍不拔的意志。故数学家的人格魅力可使学生精神达到净化和升华,身心得到和谐健康的发展。因此,学习数学史有助于学生更好地理解数学思想,而且数学发展过程的多元化、数学思考的多样性所展现出的无穷智慧,可逐渐沉积为学生的内在涵养,成为其数学素养的理论支撑[3]。
《数学史》课程评价方法既不适合以期末考试成绩作为主要评价依据,也不宜以一篇小论文确定最终成绩。课题组在讲授课程内容的同时,从学生现有认知水平出发,设定多项切实可行、生动有趣、富有创新性的任务。由教师为学生提供学习平台和学习支持,引导其以学习小组为单位,通过对信息的收集、分析、处理和总结,完成学习任务并展示其学习成果。
二、《数学史》课程评价方案
(一)课程基本评价体系
挪威数学家阿贝尔(N. H. Abel,1802—1829)曾把高斯(C. F. Gauss,1777—1855)比喻成狐狸,用尾巴抹平了自己在沙地上走过的脚印,因其著述简明扼要,未展现其最初的创新思维。而高斯却答:“凡有自尊心的建筑师,在瑰丽大厦建成之后,决不会把脚手架留在那里。”犹如数学教育家弗罗伊登塔尔(H.Freudenthal,1905—1990)云,今已把数学家的原始“火热思考”变成了“冰冷美丽”。作为行走于数学和历史之间的《数学史》课程,应注重创新人才培养,彰显其独特教育功能,充分展示数学家的思维活动,绽放数学家的创新花火,重现知识的发现过程。
人类对数与形的认识是从简单到复杂,这与学生学习数与形的顺序基本一致。远古时代的数字用来计算野果、人群、猎物数量,而几何图形则被用来测量田地、河流和绘制道路。从此,观察者、梦想人、好奇者和匠人踏入了数学领地。若想了解数学到底是什么,就必须追随其脚步,追溯那漫漫岁月。这样也有助于思考我是谁,我能干什么,我的梦想是啥?每个学生都拥有强大的学习潜能,而打开这宝库的钥匙是其发自内心的原动力。
基于建构主义成绩评价观,《数学史》课程的学生成绩评价基本方案为:以促进学生全面发展为中心,既通过评价其学习内容,也评价了知识结构;既通过评价其独立学习能力,也评价了合作学习能力;既注重对学习结果的评价,也注重对学习过程的评价;既考察其书本知识,也考察在社会实践中的表现。课程学习评价方式主要包括日常表现(占30%)、学习过程(占30%)和结果性评价(占40%)(表1)。同时,为了鼓励部分学生自主学习、脱颖而出,我们精心设计了期末考试免试条件。旨在激发学生的学习兴趣,有效调动学生学习的积极性。以本为本,促进学生主动发展和全面发展,使数学文化浸润和滋养学生的学习过程,强化学生对知识的理解和运用能力,挖掘学生自我实现的个体潜能,全面提高学生的实践能力和创新能力。满足下列条件之一者,成绩直接记为优等:
1.课堂讨论踊跃参与,并有5次以上回答具有创新思想者;
2.复原某个数学问题者,如祖冲之求圆周率的编程实现;
3.对某数学家思想有深入研究者(不是泛泛而谈,要有独到之处);
4.阅读数学经典(如《九章算术》《几何原本》《自然哲学的数学原理》)2部以上者;
5.数学史讲座优秀者,数学文化演讲优秀者;
6.数学史读书笔记、调研报告优秀者,数学文化传播和实践活动优秀者;
7.精美数学文化元素工艺品制作者;
8.其它方面相关优秀表现者。
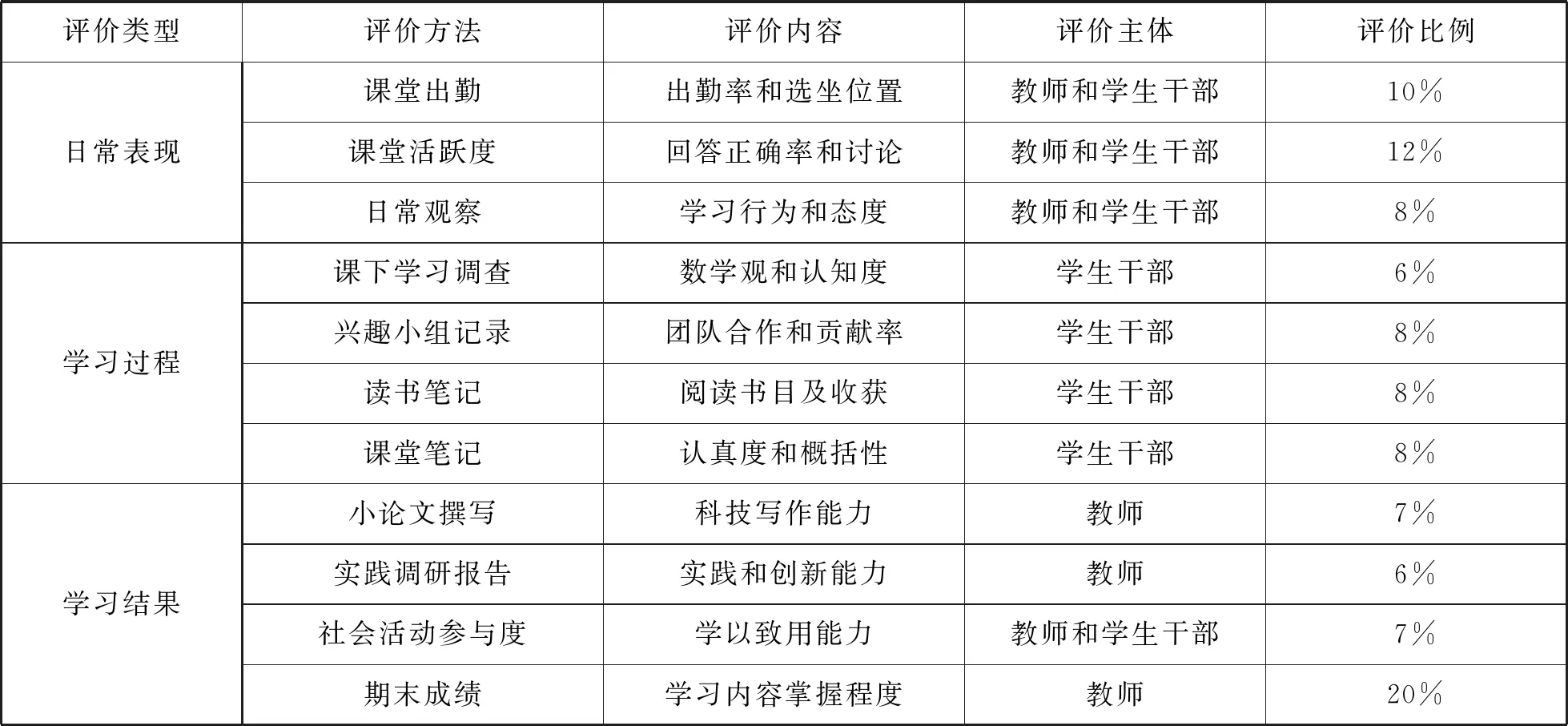
表1课程评价基本体系
(二)日常学习表现和学习过程评价
引导学生透过一些史实和现象,触摸到其蕴含的数学文化价值和数学原始理念,使其构成一种具有生命活力的积极影响。进而引导学生逐步进入广袤而深邃的数学世界,欣赏其空谷幽兰、冰山雪莲和绝顶灵芝。将学生置身于数学规则发生、发展、形成的生动过程,引导其亲历观察、猜想、验证、建模、应用等数学活动,可获得一种更有力度、充满张力的数学思考及触及心灵的精神愉悦,诚可谓“道理跃如,若指掌按图无难坐得”。开课伊始,师生分别建立《数学史》课程学习档案,以通过观察和记录学生在学习情景中完成各种学习任务时的表现来评价之。此乃监控和了解学生整个学习过程,把握其学习轨迹,进而引导学生学习反思的有效手段之一。
大约在授课三、四周后,学生已初步了解《数学史》课程内容,为培养良好团队协作精神,让其自由组合成学习讨论小组,一般7人左右,选出组长1名,分别冠以数学家名字,诸如牛顿小组、高斯小组、欧拉小组、刘徽小组和祖冲之小组等。每个小组都根据组名来确定讨论主题,精读教材相关内容,收集相关数学史资料,同时组长做好过程性学习活动记录。各成员之间既有分工又有合作,有收集资料者,有负责撰写者,有负责实验者等。大家齐心协力取得了一些可喜成绩。如:祖冲之小组给出了其求圆周率的编程程序;何承天组讨论了《元嘉历》创立的数学背景;阿基米德小组给出多种求球体积的方法;笛卡儿小组给出了一些奇思妙想等。
当然,成立学习小组并不在于学生是否能够取得研究成果,关键是让他们逐步形成了正确数学观。因而过程性评价较为全面地评价学生的研究性学习,是对学生的学习态度、学习过程和学习效果进行三位一体的评价。注重“学得好”是希望通过让学生体验参与研究性学习活动获得亲身体验,培养其认知探究方法、创新精神和实践能力。同时学生亦可及时反思自己的进步和不足,以便尽快调整学习策略和方法。
在课堂教学过程中,我们注重张扬学生的个性,吸引更多人参与到课堂讨论。每堂课我们都精心准备,反复思考以下问题如何有机融入课堂教学:
1.如何利用数学史料激发学生学习数学的兴趣,促进其不断发现问题、提出问题和解决问题;
2.如何借助数学史料激发学生主动探究的学习欲望,由“要我学”转化为“我要学”,做到上课不玩手机,认真听老师讲课;
3.如何通过数学史料来研究学生的数学认知规律,促进其实现数学认识的新飞跃,能够真正享受数学;
4.如何利用数学史料陶冶学生高尚情操,启迪其科学智慧,激励学生的创造热情,改变其固有的数学观;
5.如何通过数学史料来渗透数学思想方法,逐步提升学生的综合科学素养和数学素养。
另外,《数学史》课程“教的过程”和“学的过程”皆不能仅仅局限于课堂,故教师对学生记录档案不是简单进行等级评价,而是以学生真实学习表现纵向评价学生个人的发展轨迹(以入学成绩作为参照,对比第1、2学期考试成绩),评价亦能做到因人而异(有些学生可能高考失常,梳理其易麻痹大意之处);对于少数民族学生,尤其是维吾尔族学生因其母语不是汉语,要给予更多关爱。同时鼓励他们多多参与课堂讨论,注意挖掘自己民族的宝贵数学文化。
因此,建立《数学史》课程学习档案,不仅可评价学生在学习过程所表现出的创新精神、协作能力、实践能力,还能了解其情感态度价值观等诸多发展情况。犹如欧拉(L.Euler,1707—1783)云:“一个科学家若只是做出了给科学宝库增加财富的发现,而不能坦率阐述那引导他做出发现的思想,则其就没有给科学做出足够的工作。”[4]
(三)学习结果性评价
前苏联数学教育家苏霍姆林斯基(В.А.Сухомли нский,1918-1970)提出:“只有教师思考的大脑才能教会学生大脑的思考,同样只有喜欢学习的教师才能培养喜欢学习的学生。”[5]随着以海量、多样和高速为特征的大数据时代到来,应利用大数据的挖掘与分析指导学生学习,为每个学生量身定做学习环境与个性化活动。充分利用现代教育技术拓展学习空间,以交往学习、自主探究学习的教学理念设计教学,融知识传授、能力培养和素质提升于一体,注重理论与实践相结合、课内与课外学习相结合、面授与网络学习相结合、班级授课与小组合作交流学习相结合。根据课程内容和学生个性特征,灵活运用讲授法、讨论法、探究法、案例法、对话教学法、实践体验法等多种教学方法,调动学生积极参与学习过程,增加合作交流、自主学习的自我意识和发展愿望。[6]
《数学史》课程的评价方法从学生现有认知水平出发,设定了若干项切实可行、生动有趣、引人入胜、富有创新性的学习活动。诸如原著阅读比赛、数学史演讲、数学文化沙龙、美与数学、史料研究、数学史小品等学习活动。尤其是让少数民族学生讲解该民族的数学发展动态,既增强了他们的民族文化自信,又开阔了同学们的数学视野。
学习结果评价是对学生在学习活动结束后所获得的知识技能、思想方法、情感态度等诸多方面进行地评价,旨在考察和检测学生研究性学习后的成果和质量。对于研究性学习结果评价,我们是从整体角度,以学生的最终文字材料为基本依据进行总结性评价。学习结果有多种表现方式,可以是数学编程、数学剧目、数学诗歌、数学漫画、数学论文、读书笔记、工艺作品、数学史演讲、数学文化研究报告、研究成果现场汇报等。
对于学习结果作品进行评价时,由教师、学生代表一起对各学习小组的作品进行评价,必要时也可以邀请相关专家参加,最终给出指导性意见和建议。这样可使得每个人都能有所收获。
对于期末考试试题,我们可谓进行了精心打造。按照教学内容,命2套同等难度的覆盖整个学期授课内容的试题。其中基础题占65%,中等难度题占20%,高难度题占15%。试题遵循教学大纲的要求,注意突出重点,既要考察学生对基础知识、基本技能的识记和理解,也要检验对学生分析问题和解决问题的能力。考试题型主要包括填空题、名词解释、计算题、简答题和论述题。整套试题力求避免学生死记硬背现象,注重考察其综合科学素养和灵活应用数学思想方法的基本能力。多年教学经验、试卷分析和学生反馈已充分证实了这一点,一般成绩分布为偏正态分布。
结语
在《数学史》课程教学评价实践探索过程中,我们应注重教与学、训与练和主题研讨互相依存、互相联系,从而构成有机多元化的教学评价过程。评价主体包括教师和学生,即教师对学生的评价、学生间的相互评价以及学生的自我评价三个部分。其中教师评价与学生评价相互均衡分配,既能保证学生的主体地位,也保证了评价信息的公正与全面;既尊重学生学习的主体地位,也尊重了学生在评价中的主体地位。
通过实施《数学史》课程过程评价方式,能够体现和细化学生的学习成果,更加准确地评价学生的学习能力和创新能力。该评价体系极大调动了学生的学习积极性和参与性,使得学生不仅学习了解数学史知识,而且锻炼了其实践能力、研究能力及合作意识,最可贵的是不少学生逐渐学会了数学思考。因此,注重课程过程性评价并未把学习过程和学习成果分隔开来,而是对学习过程和学习成果的综合性评价,旨在为学生设计一条专享性路径,培养其独特性的创新素养之路。

