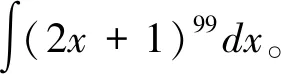不定积分第一换元积分法教学探究

周凤芹

(山东协和学院 基础部，济南 250109)

第一换元积分法也称凑微分法，它是微分公式的反向应用，要求学生熟练掌握微分公式。换元的目的是回归到基本积分公式，以起到对积分公式的巩固作用。不定积分和定积分的积分方法本质相同，不定积分计算方法的学习会直接影响定积分的学习，同时也会影响多元函数微积分的学习效果。积分的换元积分法包括第一换元积分法和第二换元积分法，其本质都是针对复合函数的积分。直接积分法是利用积分基本公式和线性性质来计算积分的方法。积分基本公式是从微分基本公式转化来的，线性性质则对应着微分运算的代数和、数乘。与微分计算相比，积分的计算更具有灵活性，直接积分法可以解决一些简单的不定积分问题。积分的第一换元积分法是基本公式的延伸，对应微分学中的复合函数求导，但其形式变化多样，掌握积分的第一换元积分法本质是初学者的难点。

1 不定积分第一换元积分法本质

同济大学第七版教材中对第一换元积分定理的描述：

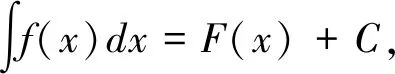
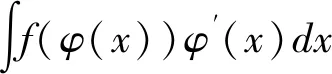
2 不定积分第一换元积分法引例

现有教材中的引例多数是对cos3x和e-3x的积分，即对比积分基本公式把dx进行变换，套进公式。此过程对凑微分法的本质理解比较生硬，对于数学基础较差的学生来说，接受度较低。于是，选择了一个学生可以结合基本积分公式和积分性质更容易计算的例子，学生可通过参与计算巩固第一节的知识，形成计算积分的技能，再把结果和公式对比，形成结论，使学生能够理解抽象的第一换元积分法概念，更容易接受换元法的应用过程，形成牢固的计算思路。

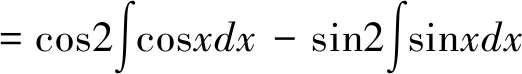
=cos2sinx+sin2cosx+C

=sin(x+2)+C

3 第一换元积分法的计算思路总结

图1 不定积分第一换元积分法的关键点Fig.1 Key points of the first integration by substitution of indefinite integral

至此，不定积分第一换元积分法的概念已形成，使用的基本思路和关键点也凸显出来。不定积分第一换元积分法的应用可以总结为四个字：设、求、代、换，具体为假设中间变量u=φ(x)，求出x=φ-1(u)和dx，代入积分并求解，用x=φ-1(u)代换u得出最后结论。