毛竹林竹鞭生长特征和空间结构的探地雷达无损探测*

熊雨露 周宇峰 李平衡 童 亮 周国模 施拥军 杜华强

(浙江农林大学省部共建亚热带森林培育国家重点实验室 浙江省森林生态系统碳循环与固碳减排重点实验室 浙江农林大学环境与资源学院 杭州 311300)

毛竹(Phyllostachysedulis)林地下竹鞭系统是由同一母竹发出的、各年龄竹鞭相互联结的组合(蔡伟国， 1986)。地下竹鞭系统在毛竹林生态系统中扮演着重要角色，它可在毛竹生长发育过程中获取水分和营养，也是支撑和固定立竹的重要器官； 竹鞭在毛竹林高效固碳过程中具有重要贡献，研究表明竹鞭系统的碳存储量约占毛竹林总碳量的40%(周国模， 2006)； 更为重要和特殊的是，竹鞭把竹林中各单株竹子连接起来，使竹子个体之间(老竹与新竹、老竹与老竹)发生着极复杂的物质和能量交换，从而实现毛竹林“爆发式生长”等高效固碳特性。深入研究毛竹林竹鞭空间结构及动态变化，是诠释毛竹林高效固碳机理过程的关键。

由于毛竹林竹鞭深入地下，观测不便，很难精确调查，导致自然条件下的竹鞭研究无论在广度和深度上均落后于地上部分(王燕等， 2008; 周本智等， 2004)。传统的竹鞭探测方法(挖根法、土壤剖面法等)虽能提供合理且精确的信息，但费时费力，还会破坏土壤环境和毛竹竹鞭，从而无法长期和重复性观测研究(周本智等， 2004)。近年来，国内外科学家发展了一系列无损根系探测方法，其中探地雷达(ground penetrating radar，GPR)是一种快速且可重复观测的地球物理技术，它利用电磁波在媒质电磁特性不连续处产生的反射和散射实现浅层成像、定位，进而实现对地表下目标的探测(Raz-Yaseefetal., 2014)。由于特有优势，GPR应用于根系探测的潜力巨大。目前主要应用于树木根系的根径大小和根系生物量估算等方面(Bassuketal., 2011; Butnoretal., 2012; 崔喜红等， 2011)。把GPR应用于毛竹林竹鞭结构的探测至今未见报道，为此，本研究基于GPR探测毛竹林竹鞭生长特征和空间结构，以期为毛竹林地下竹鞭研究提供新思路。

1 研究区概况

研究区位于浙江省杭州市临安区浙江农林大学平山实验基地(118°51′E，29°56′N)，该区属季风性气候，温暖湿润，光照充足，雨量充沛，四季分明。年均降水量1 613.9 mm，年均气温16.4 ℃，年均日照时间1 847.3 h，全年无霜期237天。样地内土壤属黄壤土，土层较厚，土壤湿润和疏松透气较好，石砾含量约10.90%。

2 研究方法

2.1 样地设置

选取3块无人为干扰的5 m×5 m毛竹林样地，样地毛竹密度4 800株·hm-2，平均胸径9.21 cm，林下伴生有稀疏草本和灌木。

2.2 雷达探测与数据采集

图1 样地测线布设情况(左上)、竹鞭挖掘情况(左下)和测线与毛竹位置示意(右)Fig.1 Layout of surveying lines in sample plot (left-upper),the excavation of bamboo rhizomes in sample plot (left lower),and the measurement lines and P. edulis positions (right)

2.3 竹鞭实地挖掘与测定

对经探地雷达扫描后的毛竹林样地，先进行每木检尺，记录胸径和年龄因子，然后挖掘样地内竹鞭，在不破坏竹鞭的基础上沿竹鞭两侧挖掘，并清除竹鞭附近的泥土，使鞭体能裸露出。随后使用全站仪，记录各条竹鞭的三维坐标信息。3块样地分别有完整竹鞭23、26和21条，根据竹鞭年龄识别特征，将完整的幼、壮、老龄竹鞭现场编号后带回实验室进一步处理。

2.4 竹鞭样本处理与测定

将竹鞭样品上附着的土壤及石块等杂质去除并置于实验台上，使用皮尺测量鞭长； 之后沿竹鞭每隔10 cm进行标记，用游标卡尺于标记处的上下左右方向分别测量3次，控制误差在1 mm以内，取测量结果均值为该部位直径，取测量结果的总体均值作为该样品直径(Cuietal., 2013)。将竹鞭样品沿标记处分割成小段，以方便使用分析天平进行鲜质量测定。将全部样品测定鲜质量后放入烘箱，先105 ℃杀青30 min，之后80 ℃烘干至恒质量，测得干质量。

2.5 雷达数据预处理与竹鞭信号提取

原始雷达图像很难提供足够的要探测目标地物的几何信息，在获取雷达数据剖面时，原始回波信号中不仅包含有目标信号，还包括收发天线之间的直接耦合波和地面反射波以及其他干扰信号等，所以雷达接收到的回波实际是一种弱信噪比、波形畸变的信号，这些都给雷达剖面的解译带来困难。因此，在进行解译之前，必须对原始雷达采集数据进行杂波处理和调整。预处理的目的是去除或尽可能地降低干扰信号成分，提高数据的信噪比，并对接收回波进行波形修正，具体需要进行初至时间拾取、系统温漂误差校正、背景杂波去除、信号增强和偏移归位处理5步预处理，在GprMax软件中完成，具体处理方法和步骤参考该软件的用户手册。图2为本试验数据的5个预处理过程，其中字母a～e分别是经过了去直流漂移、静校正、抽取平均道、巴特沃斯带通滤波和滑动平均这5步处理后的竹鞭雷达数据图。根据样地内所有扫描的雷达测线中提取的竹鞭信号所在位置与土层深度，得到样地内竹鞭的垂直与水平分布。

图2 探地雷达数据预处理过程Fig.2 Preprocessing of ground penetrating radar data

2.6 基于双曲线模型的竹鞭直径估计

按Ristic等(2009)提出的双曲线模型方法来估算竹鞭直径。根据探地雷达电磁波的传播原理，当地下目标为圆柱体时，会有如图3所示的回波双曲线模型。其中圆柱体目标物跟天线以及电磁波的传播距离满足勾股定理：

(ri+R)2=(xi-x0)+(r0+R)2。

(1)

式中：R为目标物的半径(cm)；xi为天线的初始位置(cm)；x0为天线经过时间t移动到目标物正上方的位置(cm)；ri为初始时天线和目标物之间的距离(cm)；r0为经过时间t天线和目标物之间的距离(cm)。由于电磁波从发射到接收走了往返两趟距离，所以ri=vti/2，r0=vt0/2,ti为天线位于xi时探测目标物电磁波的传播时间(s),t0为天线位于x0时探测目标物电磁波传播时间(s)。公式 (1) 可以通过R、v、x0和t0这4个参数的关系式来表示，将其展开并整理如下：

(2)

根据公式(2)可知，双曲线模型拟合需估计x0、t0、v和R这4个参数，这就把直径估算转化为双曲线拟合问题。双曲线拟合所需的数据(x,t)由雷达扫描得到，可利用雷达配套的reflexw软件来拾取； GprMax正演得到的数据需要通过Matlab编写程序进行拾取，具体方法如下： 在得到模型二维剖面图像后，使用ginput函数设置需要拾取的采样点个数，然后在双曲线上选取需要的坐标数据，数据类型为(xi，ti)。由于横坐标数据太小，所以需进行放大，将横坐标单位由m转化为cm。

4个待拟合参数中的x0和t0是双曲线的顶点，较易确定。研究目标是准确估计直径R，而波速v是未知数，错误的v取值容易导致错误的R拟合值。因此需先限定波速v的合理取值区间，从而得到精度较高的R估计值。根据试验结果及Ristic等(2009)文献中的结论，波速的最小值和最大值相差较小，例如直径10～80 mm物体的波速为5.53×107～6.68×107m·s-1。因此限定波速v的范围为[5.53×107, 6.68×107]； 然后进行双曲线模型拟合，拟合确定直径R。

2.7 竹鞭生物量拟合模型

竹鞭生物量即竹鞭的干质量(WD)。如将竹鞭的某段假设为圆柱体，那么当假设竹鞭直径为D、长度为L、密度为δ时，竹鞭生物量可简单表示为WD=1/4πD2Lδ，但实际情况并非如此，竹鞭形状不规则及竹鞭节间生长浓密细根都会影响生物量估算精度。因此需合理选择竹鞭生物量模型。

图3 双曲线模型原理Fig.3 Principle of hyperbolic model

各树种和毛竹的生物量模型种类有很多，概括起来有3类(胥辉， 1998; 曾伟生， 2011)： 幂函数模型、多项式模型和指数函数模型。借鉴立木生物量模型变量的选择，结合探地雷达容易获取的竹鞭信息，本研究构建竹鞭生物量模型时，采用的变量包括鞭长L、鞭径D及DL和D2L，并使用幂函数模型、多项式模型和指数函数模型：

BR=aDb；

(3)

BR=a(DL)b；

(4)

BR=a(D2L)b；

(5)

BR=a+bD+cD2；

(6)

BR=a+bDL+c(DL)2；

(7)

BR=a+bD2L+c(D2L)2；

(8)

BR=aebD；

(9)

BR=aebD2；

(10)

BR=aebDL；

(11)

BR=aebD2L。

(12)

式中： BR为竹鞭生物量；a,b,c为参数。

2.8 模型检验

为验证竹鞭直径模型的估计精度，随机选取10条竹鞭的雷达数据，利用双曲线模型估计其直径，并通过这10条竹鞭的实测直径值，计算模型估计直径的相对误差来检验直径模型的估计精度。

为验证竹鞭长度和空间位置(平面位置与深度)的探测精度，随机选取10条竹鞭，提取雷达数据计算每条竹鞭的长度，每条竹鞭等距离分为10段，选取每段中点的空间位置(X，Y，Z)用于检验所探测竹鞭空间位置的精度。长度和空间位置精度评价采用估计值与实测值的相对误差这一指标。

对于竹鞭生物量拟合模型，随机选取18条竹鞭作为建模样本，另外选5条竹鞭作为模型检验样本。模型建立精度与模型检验精度评价都采用确定系数(R2)和均方根误差(RMSE)这2个指标。

3 结果与分析

3.1 竹鞭直径估计

使用基于双曲线模型估算的10条竹鞭直径结果见表1。总体而言，竹鞭直径估算值和实测值较接近，误差范围为-14.45%～20.66%，估算效果很好(图4)，说明该直径模型估算有效。

表1 基于双曲线模型的竹鞭直径估计结果Tab.1 Estimation of bamboo rhizomes diameter based on hyperbolic model

3.2 竹鞭空间结构特征

根据雷达扫描数据提取竹鞭空间位置信息，并估算其直径和生物量，再按垂直分布和水平分布来分析其空间结构特征。下面以样地I (有23条竹鞭) 为例来分析竹鞭的垂直与水平分布特征，另外2块样地的结果类似，不再重复。

3.2.1 垂直分布特征 表2为样地I内所有竹鞭在4个土层的分布情况统计表。竹鞭数量的土层分布为： 0～5 cm(裸露)土层5条、5～20 cm土层9条、20～40 cm土层7条、>40 cm土层2条，说明竹鞭集中分布于0～40 cm土层，占竹鞭条数总量的91%，竹鞭的鞭长和生物量分别占总量的95%和93%。竹鞭直径分布范围为1.88～3.21 cm，4个土层的平均直径分别是2.02、2.01、2.36和2.42 cm，变化不大，但竹鞭直径在下层土壤(20～40 cm和>40 cm)明显大于上层土壤(0～5和5～20 cm)。样地内的总鞭长和生物量分别为135.2 m和2.5 kg，折合为54 080 m·hm-2和1 001.17 kg·hm-2，即竹鞭总长度与地上竹秆总长度(竹秆平均高×株数)相当，但由于竹鞭直径(平均2.15 cm)远小于竹秆胸径(平均9.2 cm)，使竹鞭总生物量要远低于竹秆。

3.2.2 水平分布特征 根据雷达扫描数据提取样地内竹鞭的空间位置信息，在忽略竹鞭的土层深度分布以后，得到竹鞭的水平分布(图5)。图5表明竹鞭在地下走势较曲折，空间分布相对均匀。同一竹鞭的直径差异不显著(P>0.5)，但不同竹鞭差异显著(P<0.01)。不同竹鞭的长度也差异较大，由于样地大小限制，有些竹鞭延伸到样地外，导致部分竹鞭不完整。同时，结合地上立竹位置可清楚看出哪些立竹属于同一竹鞭系统。从图中还可看出，不能依据立竹之间距离来判断是否为同一竹鞭相连，因为有些立竹空间位置很近却不属于同一竹鞭，有些立竹空间位置较远却由同一竹鞭相连。

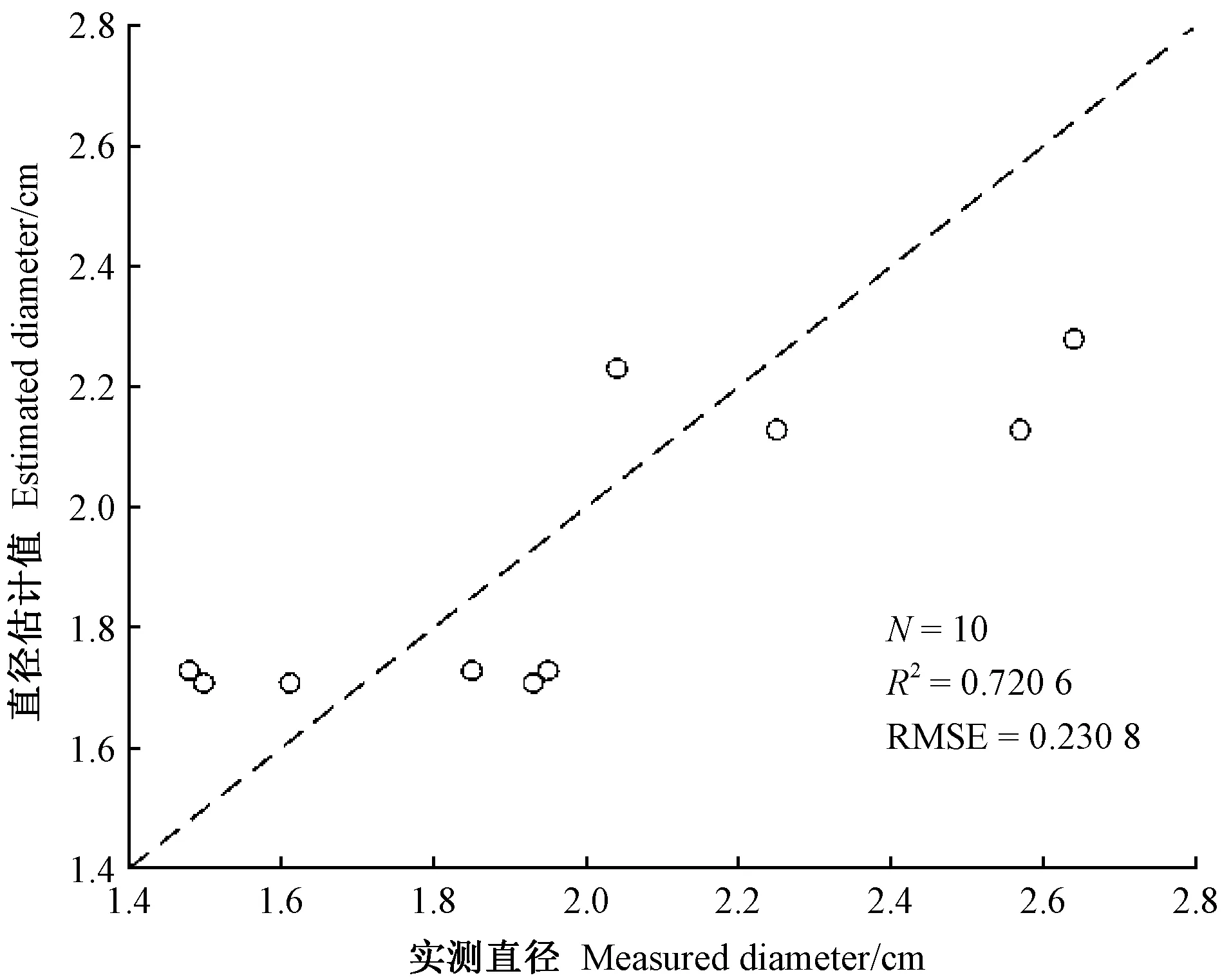
图4 实测直径与估计直径的对比 Fig.4 Comparison of measured diameter with estimated diameter

表2 竹鞭在不同土层中的分布特征Tab.2 Characteristics of bamboo rhizomes in different soil layers

图5 样地竹鞭水平分布Fig.5 Horizontal distribution of plot bamboo rhizomes

3.2.3 竹鞭长度与空间位置探测精度的检验 表3为样地内10条竹鞭的长度与空间位置探测精度的检验结果。探地雷达探测竹鞭长度的相对误差为0.53%～8.51%，空间位置X、Y、Z方向上的相对误差分别为0.13%～6.65%、1.23%～6.55%和2.42%～7.41%。竹鞭长度和空间位置的探测精度远大于竹鞭直径的估计精度，这是因为竹鞭长度一般达到1 m以上，误差相对较小； 空间位置也较好确定，误差较少； 而直径只有2～3 cm，误差相对较大。对竹鞭直径的估计精度是探地雷达应用的重要方面，也是造成竹鞭生物量估算精度误差的主要原因。

3.3 竹鞭生物量估计

3.3.1 竹鞭生物量模型的构建与检验 10个竹鞭生物量模型的拟合结果见表4。从模型的建立精度来看，10个模型的R2范围为0.61～0.95，RMSE范围为18.3～51.6 g。多项式模型和指数模型明显好于幂函数模型； 以DL和D2L为变量的模型显著好于以D或D2为变量的模型； 所有模型中以DL为变量的多项式模型和以D2L为变量的指数模型拟合效果最好，R2为0.93～0.95，RMSE为18.3～22.4 g。

从模型的检验精度来看，10个模型的R2为0.55～0.83，RMSE为17.3～48.0 g。同样也是多项式模型和指数模型好于幂函数模型，但以D2L为变量的模型显著好于以D、D2和DL为变量的模型。

综合模型建立精度与模型检验精度的结果，认为以D2L为变量的指数模型(BR=65.17e0.002D2L)最佳。

表3 竹鞭长度与空间位置探测精度检验结果Tab.3 Detection accuracy test results of bamboo rhizomes length and spatial position

表4 竹鞭生物量模型参数拟合结果Tab.4 Fitting results of model parameters of bamboo rhizomes biomass

3.3.2 基于探地雷达数据的生物量模型精度检验 表5为基于10条竹鞭的实测与估计直径及用最佳模型BR=65.17e0.002D2L计算的竹鞭生物量和实测生物量对比结果，表明用实测直径计算的生物量与实测生物量相比，RMSE为7.87～33.23 g，用估计直径计算生物量与实测生物量相比，RMSE为0.02～41.08 g，由此可见，基于估计直径和实测直径的生物量计算结果相差不大，二者没有显著差异。因此该生物量模型适用于探地雷达估计竹鞭直径作为输入数据，误差不会显著增加。

4 讨论

自20世纪60年代起我国就对毛竹林竹鞭展开研究，主要涉及竹鞭的数量(廖光庐， 1988; 郑郁善等， 1998)、空间分布(高培军等， 2003； 胡超宗等， 1994)、生长动态(吴萌等， 1984; 周本智， 2006)和生物量(陈辉等， 1998； 李振基等， 1993)等方面。研究时间集中在20世纪80—90年代到2000年初，近几年鲜有毛竹林竹鞭研究。这主要是由于试验手段限制，以及研究热点大多关注于地上生产力及其碳汇潜力而忽略了地下部分。过去竹鞭研究主要是通过挖掘法调查竹鞭，费时费力且有破坏性，而且无法重复观测竹鞭动态发展过程，造成研究无法深入和远落后于地上研究； 由于竹鞭与地上立竹是相连的整体，这也阻碍了对竹林生态系统整体高效固碳机理过程的探索。

表5 竹鞭生物量模拟结果Tab.5 Simulated results of bamboo rhizomes biomass

GPR技术应用于探测植物根系的研究始于1999年(Hruskaetal., 1999)，经过20年发展，目前可用于树木根系制图、根径大小及根系生物量的估算 (Butnoretal., 2012; Hiranoetal., 2009; 崔喜红等， 2009)。但由于一般树木根系分布土层深入地下几米甚至十几米，且以细根为主，给GPR探测带来了困难，造成探测精度有限(Cuietal., 2011)。树木根系的分布土层较深，生长方向朝下，剖面重叠度高，粗细不一等给GPR探测根系结构带来了困难，但毛竹林的竹鞭均分布在浅层土壤(大部分在0～40 cm土层)、大多是水平方向生长、竹鞭直径相对均一且较大(一般2～4 cm)，且毛竹林为单一树种，地表灌草层相对较少，因此毛竹竹鞭是GPR探测的理想对象，比其他树种根系探测要容易的多。因此，本研究发展一种基于GPR的毛竹林地下竹鞭空间结构无损探测方法，可有助于解除地下竹鞭观测的困难。

本研究表明，毛竹林的地下竹鞭较易探测，雷达信号强烈，竹鞭位置信息方便提取，从而可分析竹鞭的垂直和水平分布特征。同时可利用双曲线模型估计竹鞭直径，并进一步估计竹鞭生物量，效果都较好。因此，利用GPR探测毛竹竹鞭空间结构及生物量是可行的。

基于本研究发展的毛竹林竹鞭GPR探测方法以及竹鞭直径与生物量模型，下一步还需要在各种野外条件下开展大量研究和应用，来检验和完善该方法与模型。比如不同经营历史、经营类型、经营强度毛竹林分的应用精度是否有差异，不同土壤类型、土壤质地、土壤水分条件对该应用是否有影响，等等。另外，毛竹林地下部分除了有较易利用探地雷达探测的竹鞭，还有大量较难精确探测的细根，下一步还需通过挖掘试验分析竹鞭和细根的空间分布关系以及二者生物量的比例关系，然后通过竹鞭生物量及其空间分布来估计细根生物量及其空间分布，并在此基础上，进一步探讨不同经营历史、经营类型、经营强度等对竹鞭空间结构及动态变化的影响，以及地下竹鞭与地上立竹的相互关系及其动态规律等。

5 结论

本研究发展了一种毛竹林地下竹鞭空间结构的GPR无损探测方法，可利用GPR探测地下竹鞭的位置信息，得到竹鞭垂直和水平方向的空间结构； 同时建立了估计竹鞭直径、长度、生物量的模型，拟合效果较好。但还需通过大量不同野外条件的研究和应用来完善提出的方法和模型，提高其可靠性以及精度。