最优化问题的二阶最优性条件中临界锥不同表达形式的研究
曲皓月,张 杰,王梦茹
(辽宁师范大学 数学学院,辽宁 大连 116029)
非线性规划是带有等式和不等式约束的约束优化问题,是最优化理论中较常见的一种数学模型,在交通运输、物流管理、投资组合等诸多社会经济生活领域有重要的应用。对非线性规划最优性条件的研究已经相当成熟,可见于各种优化方法的教材,如文献[1-5]。但在这些教材中对非线性规划二阶最优性条件的描述中,所涉及到的临界锥有着多种不同的表达形式,初学者在接触这部分知识时可能会感到困惑。因此归纳出不同教材中临界锥的不同表达形式并对它们之间的联系进行研究是非常有意义的,这会让初学者对临界锥及二阶最优性条件有更深层次的理解,并使得二阶最优性条件有统一的表达式。本研究考虑如下形式的非线性规划问题:
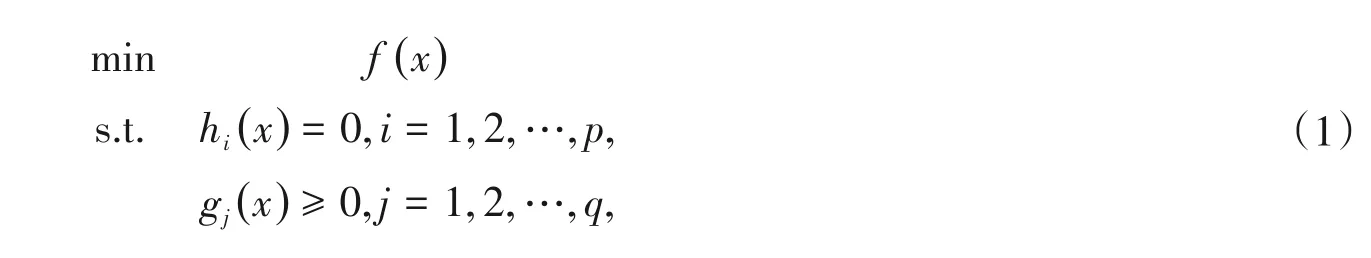
其中,f,hi,i= 1,2,…,p,gj,j= 1,2,…,q是Rn到R 的映射且二次连续可微,总结了不同教材中临界锥的六种表达形式,给出了这些集合之间的联系,并给出这些集合相等的充分条件。文章安排如下:第一节给出预备知识,接下来在第二节中给出主要结果。首先给出一些预备知识。
1 预备知识
本节给出的预备知识主要来自于国内外优化方法的经典教材和专著,见文献[1-7]。点x∈Rn被称为问题(1)的可行点,如果x满足(1)的约束条件。所有可行点所组成的集合称为可行域,记(1)的可行域为X,

则称d是X在x*处的线性化可行方向,X在x*处的所有线性化可行方向的集合记为LFD(x*,X)。
定义4 设x*∈X,d∈Rn,如果存在序列dk(k= 1,2,…)和δk>0(k= 1,2,…)使得x*+δkdk∈X,∀k且有dk→d和δk→0,则称d是X在x*处的序列可行方向,X在x*处的所有序列可行方向的集合记为SFD(x*,X)。
注意到根据文献[3]中的定义,LFD(x*,X)和SFD(x*,X)中不含有零方向,但在文献[4]和文献[6]的定义中,这两个集合含有零方向。本研究采用了后者的定义,原因是此时的方向集合是闭集合,方便后续的研究,也与锥优化中线性化切锥和切锥的定义相一致。
定义5 设Y是有限维Hilbert空间,Z是Y中的闭子集,x∈Z,则Z在x处的切锥定义为


2 临界锥不同表达形式的相互关系



所以得到C(x*)⊆S(x*,μ*,λ*),证毕。
如果线性无关约束规范不成立时,会存在d∈F(x*,μ*,λ*)但d∉S(x*,μ*,λ*)的情况,本研究引用文献[8]中用来研究Guignard约束规范的例子进行说明。
例1 考虑下述优化问题:

证明 由定理1 只需证明C(x*)⊆F(x*,μ*,λ*),根据文献[6]中的定理8.2.7 可知在M-F 约束规范下,LFD(x*,X)= SFD(x*,X)=TX(x*),所以根据定理1 中(vii)的后半部分证明直接得到C(x*)⊆F(x*,μ*,λ*),证毕。
3 结论
本研究总结归纳了不同最优化方法教材中的临界锥的表达形式,给出了这些临界锥的关系,并得到了保证这些临界锥相等的充分条件。

