一类带阻尼项非线性分数阶微分方程的振动性

曾文君，李德生

（沈阳师范大学数学与系统科学学院，辽宁沈阳110034）

非线性微分方程解的振动性广泛应用于自然科学和工程技术等领域，大量学者致力于此方面的研究。杨甲山［1-2］研究了二阶非线性中立型泛函微分方程的振动性、二阶Emden-Fowler型非线性变时滞微分方程的振动性，张晓建［3］研究了二阶Emden-Fowler型变时滞中立型微分方程的振动性，曾云辉等［4］研究了偶数阶半线性泛函微分方程解的振动准则，还有很多关于非线性微分方程解的振动性研究［5-9］，但对非线性分数阶微分方程解的振动性研究较少。

CHEN［10］考虑非线性分数阶微分方程

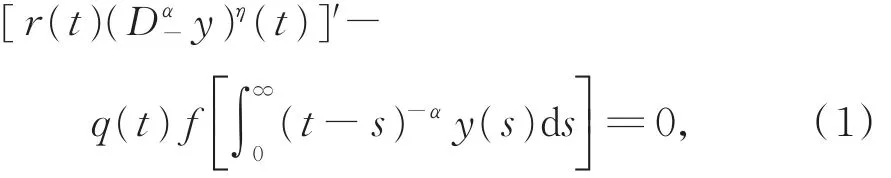
其中，Dα-y是关于y的阶为α的刘维尔右分数阶导数，α∈(0，1)，η＞ 0是正整奇数的商，对t0＞ 0，r和q为 [t0，∞)上的连续函数，k，其中，u≠ 0，k为正常数，利用 Riccati变换和不等式技巧，可得到关于微分方程（1）的一些振动性准则。

文献［11］研究非线性分数阶微分方程

本文主要研究微分方程

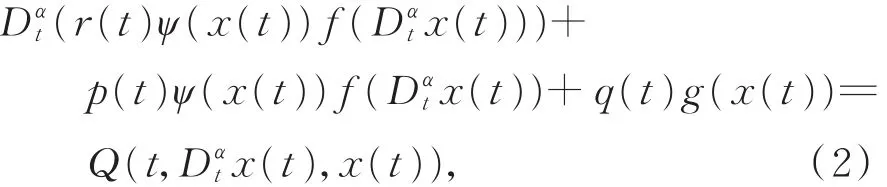
其 中 ，t∈[t0，∞ )，t0≥ 0，r(t)∈Cα([t0，+ ∞ )，R)，p(t)，q(t)∈ C([t0，∞ )，R)，f，ψ，g ∈C(R，R)，Q 为[t0，∞ )× R2上 的 连 续 函 数 ，(·) 为 修 正 的Riemann-Liouville分数阶导数，α∈(0，1)。

同时，假设下列条件成立：

(A1)r(t)＞ 0，t∈[t0，+ ∞ )；

(A2)对任意的x(t)∈R，有0＜ ψ(x(t))≤ k1；

(A3)对 任 意 的 y∈R，有 f2(y)≤lyf(y)，其中，l＞ 0；

(A4)对任意的x≠ 0，有0＜ k≤ g"(x)；

(A5)存在函数v(t)，对任意的x≠0以及任意的y∈R，有Q

(A6)对任意的x≠ 0，有

(A7)存在函数φ(t)，对任意的x≠0以及任意的y∈R，有

1 预备知识

定义1 关于t的α阶修正的黎曼刘维尔分数阶导数的定义以及重要性质［12］：

定义2［6］方程的解是振动的，是指方程的非平凡解有任意大的零点，否则是非振动的。若方程的所有解都是振动的，则称该方程是振动的。

定 义 3［6］假 设 D={(t，s)：t≥ s≥ t0}，D0={(t，s)：t＞ s≥ t0}，存 在 函 数 H ∈C(D，R)，如 果满足：

（i）H(t，s)＞ 0 在 D0上成立，对任意的 t≥ t0，有 H(t，t)=0；

（iii） 若 存 在 函 数 h(t，s)∈C(D，R)，有=-h(t，s) H(t，s)，则认为函数 H 属于Ω类，记作H∈Ω。

为方便，在下文中，定义：

2 主要结果

定理1 假设(A1)～(A5)成立，如果存在H∈Ω和 ρ∈ Cα([t0，+ ∞ )，R+)，满足：

与式（11）矛盾，假设不成立。

证毕。

3 例 子