ZPW-2000A调谐区SVA阻抗值对调谐区品质因数的影响分析

黄文轩

(中铁第一勘察设计院集团有限公司，西安 730000)

无绝缘轨道电路按照原理可以分为电气隔离式和自然衰耗式两种轨道电路[1]，前者又称为谐振式轨道电路。对于谐振电路而言，品质因数Q的高低是衡量该电路的一个重要指标，Q值越高，电路的信号选频性能越好，越容易滤除干扰，也越趋于稳定。

ZPW-2000A是国产化谐振式无绝缘轨道电路的一种，该种轨道电路的绝缘节为电气绝缘节，主要由调谐单元、空心线圈及29 m钢轨组成[2]，其中调谐单元又可以分为二元件F1型调谐单元BA1，三元件F2型调谐单元BA2。其中BA1主要用在较低频率 1 700 Hz 和 2 000 Hz 所在区段，BA2 主要用在较高频率 2 300 Hz 和 2 600 Hz 所在区段。BA1由电感L1和电容C1组成；BA2由电感L2和电容C2、C3组成。国内学者对 1 700 Hz 和 2 300 Hz进行建模[2-5]，通过建模分析了轨道电路电气绝缘节故障，补偿电容故障等方面的问题。通过分析调谐区的电气模型，利用电路理论，给出调谐单元元件参数与空心线圈阻抗值的关系，通过MATLAB软件仿真，获得良好的品质因数。

1 ZPW-2000A电气绝缘节工作原理

ZPW-2000A电气绝缘节通过谐振电路完成相邻轨道电路电气隔离。

如图1所示，以1G和3G两个相邻下行区段为例，1G轨道电路发送载频f1为1 700-1 Hz，3G轨道电路发送载频f2为2 300-1 Hz，1G和3G用电气绝缘节隔离。

图1 电气绝缘节（调谐区）原理图Fig.1 Electrical insulated joint (tuning zone) principle diagram

在频率f1为1 700-1 Hz时，得到调谐区等效电路如图2所示。F1型BA呈容性，F2型BA由于电感L2和电容C2串联谐振，阻抗值为0，等效为短路线，称其为“零阻抗”。此时钢轨电感Lg、空心线圈SVA电感Ls和F2型BA“零阻抗”等效为电感电路，与F1容性电路相并，呈并联谐振，导纳值之和为0，阻抗值理论上呈无穷大，实际值为2 Ω左右，称其为“极阻抗”。

同理，如图3所示，在频率为2 300-1 Hz时，F2型BA呈容性，F1型BA由于电感L1和电容C1串联谐振，成“零阻抗”。此时钢轨、空心线圈SVA和F1型BA等效为电感电路，与F2容性电路相并，呈并联谐振，导纳值之和为0，成“极阻抗”。

图2 载频1 700-1 Hz对应调谐区等效电路图Fig.2 Equivalent circuit diagram of the tuning zone corresponding to carrier frequency of 1700-1Hz

图3 载频为2 300-1 Hz时调谐区等效电路图Fig.3 Equivalent circuit diagram of the tuning zone corresponding to carrier frequency of 2 300-1Hz

2 谐振电路的品质因数

2.1 品质因数的定义

一个由电感、电容和电阻组成的无缘二端网络，在某一频率下，出现输入电流和输出电压同相的情况，这种现象称为谐振，该频率称为谐振频率。谐振电路可以从不同频率的信号中挑选出一个或一带频率有用的信号，具有选频或滤波的作用。

谐振频率是根据电路参数L和C确定，而衡量谐振电路选频效果的重要指标是该电路的品质因数Q。品质因数Q的广义定义为谐振时L或C无功功率的绝对值与谐振时电路损耗的有功功率之比[6]。谐振电路的频率特性如图4所示，由图可知品质因数越高，曲线越尖锐，信号的选频性能越好[7]。

2.2 品质因数的计算

根据经典电路理论可以得到串联谐振电路和并联谐振电路的品质因数为：

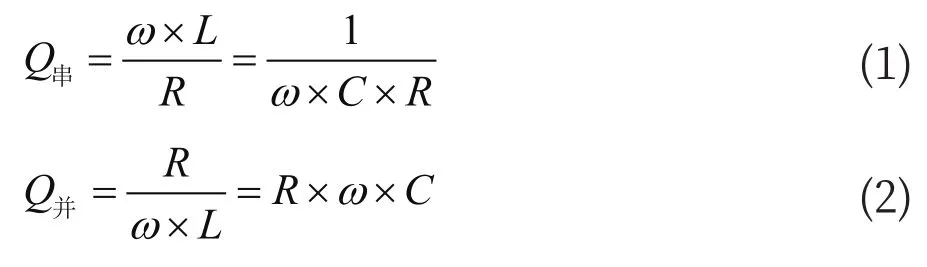
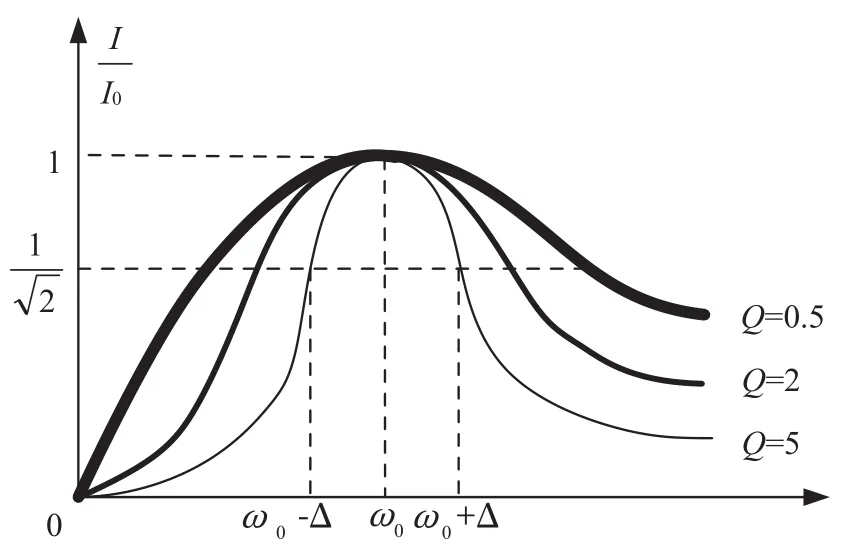
图4 串联谐振电路的频率特性Fig.4 Frequency characteristics of series resonant circuits

但是对于复杂的调谐电路，可以将其分解为两部分，电容串电阻和电感串电阻两部分。然后可以根据最后需要的电路模型，将其整合为标准的串联谐振电路或并联谐振电路，再根据公式（1）或（2）求得Q值。其中最重要的步骤是串联电路变并联电路，因此设串联电路A+Bj和并联电路C||Dj等效，可以得到以下公式：

根据公式(3)可以得出并联改串联公式：

串联改并联公式：

3 ZPW-2000A电气绝缘节建模仿真

3.1 调谐区建模

谐振电路根据电容、电感和电阻的连接方式可以分为两类，一种是串联谐振，另外一种为并联谐振。ZPW-2000A无绝缘轨道电路的调谐区恰好包含以上两种谐振方式，分别是“零阻抗”和“极阻抗”。“零阻抗”在对应频率谐振后呈短路线，防止相邻两区段信号电干扰；“极阻抗”在对应频率谐振后近似为开路，减小对本区段信号的损耗。

国内学者在调谐区小轨道电路建模时，为求取结果方便，常常忽略调谐区钢轨连接线电阻值、钢轨电阻值、空心线圈电阻值，而且在实际钢轨连接线使用的过程中，BA和SVA均通过两根并行的钢轨引接线接至钢轨。虽然仿真计算后的L1、C1、L2、C2、C3数值和普速铁路维规中给定的标准数据误差不大，但是这种模型却无法计算调谐区品质因数，所以本文给出较为详细的小轨道电路建模，如图5所示。

图5 调谐区小轨道电路建模Fig.5 Small rail circuit modeling in tuning zone

其中Rt和Lt是钢轨连接线的电阻值与电感值，Rg和Lg是钢轨的电阻值和电感值，Ls和Rs是空心线圈的电阻值和电感值。

3.2 调谐单元各参数计算

在实际设计过程中空心线圈SVA作为谐振回路的电感，可提高电气绝缘节（调谐区）谐振的品质因数[8]，平衡牵引电流，保证设备和人身安全。因此，本文根据普速铁路维护规则给出的相关参数，对调谐区重新建模，以空心线圈阻抗为自变量，计算不同频率下调谐单元L1、L2、C1、C2、C3的相应公式，并对品质因数进行求取。本文以1 700和2 300 Hz 为例，2 000 和 2 600 Hz 公式与之相同。

3.2.1 1 700 Hz时调谐区电气特性

调谐区按照电路的感性和容性可以分为两部分。一部分是F1型BA，在1 700 Hz时呈容性；F2型BA此时呈串联谐振，故另一部分由钢轨电路、空心线圈SVA和F2型BA组成，它们等效呈感性电路。这两部分电路相并，呈并联谐振，调谐区的导纳值之和虚部为零，等效电路如图6所示。

图6 1 700 Hz对应调谐区等效电路图Fig.6 Equivalent circuit diagram of the tuning zone corresponding to 1 700 Hz

根据图6可以推出以下公式：

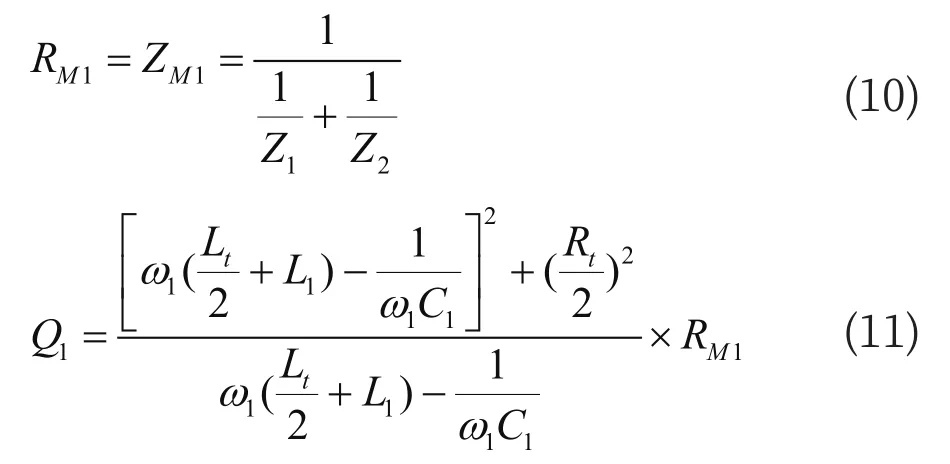
其中，ω1为 1 700 Hz的角频率；Z1为 F1型BA与钢轨连接线总阻抗；Z2为钢轨电路、空心线圈SVA、钢轨连接线和F2型BA等效阻抗；Yv为空心线圈与14.5 m钢轨和F2型BA等效导纳；ZM1为调谐区总阻抗值；RM1为极阻抗值，理论值相等；Q1为品质因数。

3.2.2 2 300 Hz时调谐区电气特性

对于F2型BA，在2 300 Hz时呈容性；此时F1型BA呈串联谐振，钢轨、SVA和F1型BA等效为感性电路。这两部分电路相并呈并联谐振，调谐区导纳之和虚部为0，等效电路如图7所示。

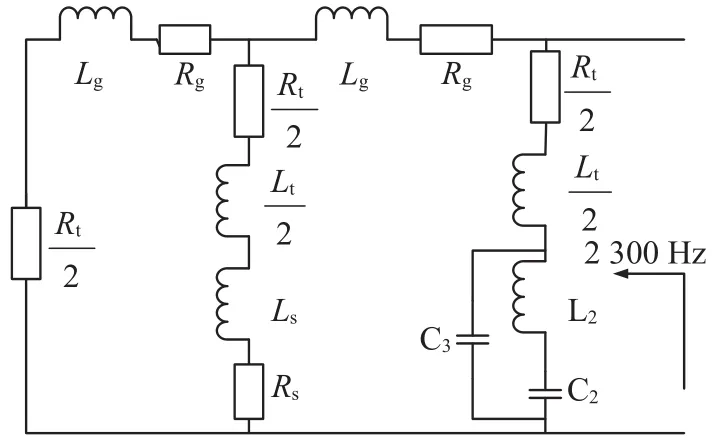
图7 2 300 Hz对应调谐区等效电路图Fig.7 Equivalent circuit diagram of the tuning zone corresponding to 2 300 Hz

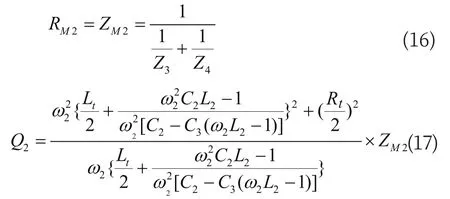
其中，ω2为 2 300 Hz的角频率；Z3为 F2型BA与钢轨连接线总阻抗；Z4为钢轨电路、空心线圈SVA、钢轨连接线和F1型BA等效阻抗；Yw为空心线圈与14.5 m钢轨和F1型BA等效导纳；ZM2为调谐区总阻抗值；RM2为极阻抗值，理论值相等；Q2为品质因数。

3.3 建模验证

图5所示模型是以工程背景为基础建立的，其中钢轨阻抗和钢轨连接线参数均参考国标值，对该模型进行电气分析后，比对各元件参数国标参考值，分析其精确性以及规律性。

3.3.1 调谐区各元件参数求取

在实际设计过程中，调谐区各元器件参数值有Ls、Rs和C23 个量取经验值，Ls为 33 μH，Rs为4.5 mΩ，C2为 90.9 μF。其中Rg，Lg各频率取值如表1所示，Rt，Lt各频率取值如表2所示。

表1 混凝土桥梁地段钢轨参数[9]Tab.1 Rail parameters of concrete bridge section

对公式(6)进行变换，可将其等效为：

其中，XC1为Z1等效容抗；R1为等效电阻。

然后对公式(9)进行变换，可将其等效为：

表2 连接线电感、电阻参考值Tab.2 Reference value of inductance and resistance of connection line

其中，Y2为Z2对应的导纳；BL2为Z2等效电纳；G2为等效电导。由于并联谐振电路要求总导纳虚部为0，所以可以得出：

针对新课改下对于语文教学的改革与创新，要求教师在课堂教学中充分运用各种资源和活动形式，激发学生的学习兴趣。在学习不同题材的语文知识时，教师不能一味进行枯燥的文字解说，或仅是单纯地自我讲述，不与学生进行交流和互动。例如，在学习诗歌散文类的文章时，教师习惯于使用传统的教学方式，对文章内容进行分析和解说。这个过程就限制了学生的思维，使学生无法与老师思想同步。应当进行角色扮演或者举办诗歌朗诵的赏析会，让学生真正地融入课堂内容中，品读作者当时的心境与语境。

由此可解出L1和C1的值。同理，也可以解出L2、C2和C3的值。频率为 1 700 和 2 300 Hz 时，求出调谐单元各元件值如表3所示。

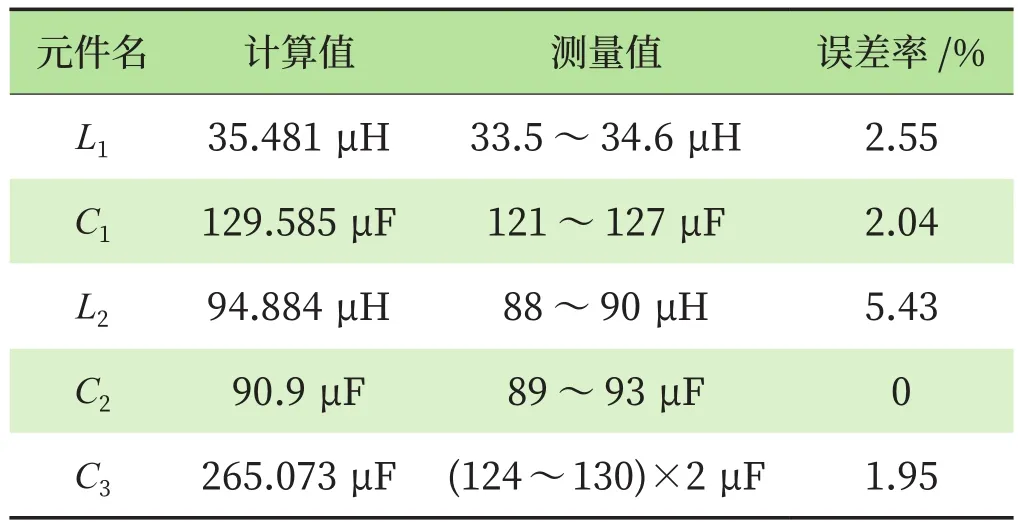
表3 1 700、2 300 Hz调谐单元元件参数值Tab.3 1 700 Hz and 2 300 Hz tuning element parameter value

由于未考虑电感L1，L2，C1，C2，C3元件自身的电感电阻和电容电阻值，所以与测量值存在小范围的误差(2%～6%)，然后再计算，容性调谐单元阻抗，如表4所示，与容性调谐单元阻抗值表[10]进行对比。

通过对比阻抗值，发现计算值与测量值的误差保持在5%以内，结合之前的对比数据，得出该组数据比较接近现场数据。

国内学者对ZPW-2000A型无绝缘轨道电路调谐单元建模后，得出的元件参数数据如表5、6所示。

表4 容性调谐单元阻抗值Tab.4 Impedance value of capacitive tuning unit

表5 文献[1]中1 700、2 300 Hz调谐单元参数Tab.5 1 700 Hz and 2 300 Hz tuning element parameters

表6 文献[4]中1 700、2 300 Hz调谐单元参数Tab.6 1 700 Hz and 2 300 Hz tuning element parameters

由于以上两位学者在建模过程中，对钢轨和钢轨连接线的自身电阻以及钢轨引接线的连接方式考虑不充分，使得误差较大。

3.3.2 空心线圈阻抗与BA各元件参数的关系

在保证电路谐振的前提下，通过MATLAB仿真空心线圈电阻值和电感值变化，观察对调谐单元元件参数值的影响。如图8、9、10和11可以看出，空心线圈的电感值变化对谐振电路元件影响远高于电阻值变化。

图8 空心线圈阻抗值对L1感值影响Fig.8 Influence of impedance of air core coil on L1 inductance

图9 空心线圈阻抗值对C1容值的影响Fig.9 Influence of impedance of air core coil on C1 capacitance

图10 空心线圈阻抗值对C3容值的影响Fig.10 Influence of impedance of air core coil on C3 capacitance

在谐振电路中电感值和电容值总是处于一种平衡状态下，相对而言电阻的变化对感值和容值影响较小。由于空心线圈作为一个感性元件存在，其感抗增大势必要引起相对应的容抗增大，所以C1和C3的电容值变小，容抗增大。同时要保证L1与C1的串联谐振，故L1感值增大；在实际工程中，由于C2的容值为固定经验值，与之串联的L2要保证谐振效果，所以该值变化幅度较小。

图11 空心线圈阻抗值对L2感值的影响Fig.11 Influence of impedance of air core coil on L2 inductance

3.3.3 调谐区品质因数与极阻抗

调谐区作为一种谐振电路，也有与之对应的品质因数，例如在频率为1 700 Hz情况下，通过公式(6)和公式(9)得到调谐单元对应阻抗Z1和Z2，通过串并联互换公式(5)将其等效为经典并联谐振电路，通过公式(2)，计算出调谐单元品质因数；调谐区极阻抗为并联谐振后等效阻抗的值，约2 Ω，可由公式(10)得出，图5所建模型计算得到的品质因数如表7所示。

表7 调谐单元品质因数与极阻抗计算值Tab.7 Tuning element quality factor and pole impedance calculation value

3.3.4 SVA阻抗值对调谐单元品质因数的影响

图12 SVA阻抗值变化对Q值的影响Fig.12 Influence of SVA impedance variation on Q value

通过MATLAB仿真空心线圈电阻值和电感值变化，观察并分析它对调谐单元品质因数的影响，通过观察仿真图形如图12所示发现SVA电感自身电阻值与品质因数成负相关的关系。因为空心线圈电阻增大，整体电阻增大，分析并联谐振品质因数计算公式(2)，可得到电阻和品质因数成负相关关系；还可以发现随着空心线圈感值增长，在1 700 Hz条件下，调谐单元品质因数在 20 μH 处获得最大为 8.636 1，经验值为 33 μH，结果为8.381 3。

4 结论

本文通过对ZPW-2000A型无绝缘轨道电路调谐区建模和仿真，分析空心线圈阻抗值对调谐单元电气参数的影响得出：空心线圈的电阻值对整个调谐区各元件参数值影响较小。但是如果忽略空心线圈电阻，则会影响调谐单元品质因数，直接影响选频效果；空心线圈电感值对整个调谐区元件参数影响较为明显，并且随着SVA电感值的变化，调谐单元品质因数在范围内可取极值。在实际工程应用中，如果确定了钢轨阻抗和调谐区长度，可以通过该仿真获得谐振效果优秀的各元件具体参数值。