非平稳信道下LDPC码低复杂度滑窗置信传播联合信道估计与译码算法

杨 洋 方 勇 单博炜

(长安大学信息工程学院 西安 710064)

1 引言

由于移动通信系统对高吞吐率的需求不断增长，具备高译码并行度的LDPC码取代了Turbo码被第5代移动通信技术标准(5G New Radio, 5G NR)所采用。此外，与Turbo码相比，LDPC码还具有更高的编码增益，更高的译码运算效率，以及更低的错误平层等优势[1]，并将继续成为下一代移动通信技术标准中信道编码方案的有力竞争者。

自5G NR开始，移动通信系统需支持更多新应用场景下的可靠通信，特别是高速移动场景，例如高速铁路、车载自组织网络(Vehicular Ad hoc NETworks, VANETs)、无人机(Unmanned Aerial Vehicles, UAVs)等。在高速移动场景下，信道呈现时变的非平稳特性，这给信道估计带来很大挑战，因为过大的信道估计误差会导致LDPC码置信传播(Belief-Propagation, BP)译码的性能恶化[2]。

常用的信道估计方法可根据是否依赖导频信号分为两类。一类是基于导频辅助的方法，包括最小二乘估计、最小均方误差估计和最大似然估计等。采用连续消除类译码算法[3,4]的极化码常采用此类信道估计方法[5]。然而在非平稳信道条件下，若要利用基于导频辅助的方法准确追踪时变的信道状态将导致大量的导频开销，从而降低传输效率。另一类是不需要或仅需要极少量导频辅助，主要发掘接收信号本身所蕴含信道信息的盲信道估计方法，这类方法更适合非平稳信道条件下的信道估计。文献[6]针对极化码提出一种可输出软信息的连续消除列表译码算法, 并通过盲信道估计与信道译码之间的迭代实现联合信道估计与译码(Joint Channel Estimation and Decoding, JCED)。LDPC码的BP译码本身就是可输出软信息的迭代译码算法，因此也可实现JCED：文献[7]将基于重要性重采样的盲信道估计与BP译码相结合，文献[8]将基于粒子滤波的盲信道估计与BP译码相结合来实现JCED。当然，也存在不与BP译码相结合的盲信道估计，例如文献[9]提出的基于最大熵定理的盲信道估计方法。此外，若译码器不需要信道信息，则不必进行信道估计，称为非相干传输[10]。文献[11,12]实质上提出一种需借助极少量导频符号来初始化列表译码器的非相干传输方案，主要适用于极短码。文献[13]提出的基于深度学习和字典学习的LDPC码译码方案，将译码问题转化为图像去噪问题处理，不存在信道估计过程，因此也可看作一种非相干传输方案。

在5G移动通信系统中，即使在sub-6 GHz频段，若相对移动速度达到300 km/h，所带来的多普勒扩展也足以导致信道状态在103bit的传输时间内发生变化。也就是说，若码长超过103，则在1个码字的传输时间内会经历不同的信道状态。然而现有文献在解决非平稳信道条件下的信道估计问题时，大多假定信道状态在同一码字的传输时间内保持不变[7,9]。文献[8,13]提出的方法虽无此假定，但无论是粒子滤波还是深度学习，在应用时都面临计算复杂度过高的问题。为解决高速移动场景下的信道估计与译码问题，本文基于信源编码中用于信源参数估计和信源相关性估计的滑窗置信传播(Sliding-Window Belief-Propagation, SWBP)算法[14,15]，提出一种非平稳信道下LDPC码的JCED算法，同时提出两种低复杂度的自适应滑窗长度设置方法。通过对不同码长、不同码率、规则与非规则LDPC码的仿真，全面评估所提算法的性能。另外，还对所提算法的初值敏感性和错误平层等问题进行研究。

2 基于SWBP的JCED算法

SWBP是处理信源编码中非平稳信源的参数估计问题[14]以及信源之间的非平稳相关性估计问题[15]的有效方法。本节将该方法进行扩展，用来解决非平稳信道下LDPC码的联合信道估计与译码问题，提出基于SWBP的JCED算法。并对信道估计时计算复杂度较高的关键步骤-自适应滑窗长度设置问题进行研究，提出两种低复杂度的自适应滑窗长度设置方法。

2.1 信道模型和符号说明

T 表示所设定的最大JCED迭代次数。

2.2 基于SWBP的JCED算法

2.3 基于滑窗的信道估计算法

3 仿真结果与分析

本节中，将利用不同码长、不同码率、规则与非规则LDPC码对所提基于SWBP的JCED算法进行全面的评估。为排除不同码结构对性能的影响，专注于评估JCED算法本身，仿真用到的规则码均采用渐近边增长(Progressive Edge Growth, PEG)算法构造；为了兼顾检验错误平层，仿真用到的非规则码采用CCSDS标准[16]中官方验证过错误平层性能的AR4JA码。

3.1 (1024, 3, 6) LDPC码的仿真

在本小节中，利用码长较短、码率适中的(1024,3, 6)码完成平方搜索交叉熵滑窗长度设置方法的有效性验证；完成基于多种滑窗长度设置方法的JCED算法的相对时间复杂度比较；完成基于DFT滑窗长度设置方法的JCED算法对局部噪声方差初始估计值的敏感性验证；对基于多种滑窗长度设置方法的JCED算法的BER性能、平均迭代次数做初步评估。

图1给出了基于多种滑窗长度设置方法的JCED算法的BER性能曲线。由图中可知：基于平方搜索交叉熵滑窗长度设置方法的JCED算法性能与基于全搜索交叉熵滑窗长度设置方法的JCED算法性能几乎相同，考虑到平方搜索相对于全搜索在计算效率上的巨大提升，在随后的仿真中，交叉熵滑窗长度设置方法均采用平方搜索的实现方式；另外，基于DFT滑窗长度设置方法的JCED算法性能与基于交叉熵滑窗长度设置方法的JCED算法性能几乎相同，在BER= 10−5时，与理想估计(即已知局部噪声方差)条件下的BP译码算法相比仅有0.25 dB的性能差距，而与仅已知局部噪声方差的均值的BP译码算法相比可获得1.2 dB的性能增益。

图1 多种滑窗长度设置方法下的算法BER性能

图2给出了基于多种滑窗长度设置方法的JCED算法的平均迭代次数曲线。由图中可知：基于DFT滑窗长度设置方法的JCED算法的平均迭代次数与基于交叉熵滑窗长度设置方法的JCED算法的平均迭代次数几乎相同，在BER= 10−5时，仅比理想估计条件下的BP译码算法的平均迭代次数多5%～6%。

图3给出了基于多种滑窗长度设置方法的JCED算法单轮迭代的相对时间复杂度。计算方法是：在仿真中不设置迭代中止条件，使1帧数据在相应JCED算法下持续迭代105轮并记录运行时间，该运行时间除以1帧数据在BP译码算法下持续迭代105轮的运行时间所得的商即为相应JCED算法的相对时间复杂度。该指标可直观反映JCED算法单轮迭代的计算复杂度。由图中可知，基于全搜索交叉熵滑窗长度设置方法的JCED算法的计算复杂度是不可接受的；采用平方搜索后，计算复杂度下降巨大，但信道估计部分的计算复杂度(355%-100%=255%)仍然超过译码部分(100%)；而基于DFT滑窗长度设置方法的JCED算法，其信道估计部分的计算复杂度(122%-100%=22%)仅为译码部分(100%)的22%，考虑其带来的性能增益，计算复杂度的提升程度是完全可以接受的。

图2 多种滑窗长度设置方法下的算法平均迭代次数

图3 多种滑窗长度设置方法下的算法相对时间复杂度

图4给出了不同局部噪声方差初始估计值下，基于DFT滑窗长度设置方法的JCED算法的BER性能。由图中可知，即使( Eb/N0)nom失 配达到±10lg4=±6 dB，对BER性能也几乎没有影响，说明基于DFT滑窗长度设置方法的JCED算法有着很强的鲁棒性。基于交叉熵滑窗长度设置方法的JCED算法也有类似的结论，这里不再赘述。

图5给出了不同局部噪声方差初始估计值下，基于DFT滑窗长度设置方法的JCED算法的平均迭代次数，由图中可知，与BER性能不同，平均迭代次数对 (Eb/N0)nom失配是敏感的：在BER=10−5时，若失配3 dB，则平均迭代次数增加41%，若失配6 dB，则平均迭代次数增加69%；若失配-3 dB，则平均迭代次数增加15%，若失配-6 dB，则平均迭代次数增加32%。总之，失配程度越高，平均迭代次数增加越多；相同失配程度下，低估 σ¯2(即失配为正值)比高估σ ¯2(即失配为负值)会导致平均迭代次数更多地增加。更多的平均迭代次数意味着更高的时延、更低的吞吐量、更大的能耗。因此，若条件允许，应尽量保证 σ¯2的估计精度，特别是对时延、吞吐量及能耗敏感的应用，尤其应尽量避免低估 σ¯2。基于交叉熵滑窗长度设置方法的JCED算法也有类似的结论，这里不再赘述。

图4 不同局部噪声方差初始估计值下的算法BER性能

图5 不同局部噪声方差初始估计值下的算法平均迭代次数

3.2 不同码长、不同码率、规则与非规则LDPC码的仿真

在5G NR[1,17]中，由于需要满足多样的业务需求和应对多变的传输环境，所采用的LDPC码的码长、码率跨度非常大。下一代移动通信同样需要很大的码长、码率变化范围。因此，有必要对不同码长、不同码率、规则与非规则的LDPC码在所提基于SWBP的JCED算法下的性能做全面的评估。

3.2.1 不同码长LDPC码的仿真

图6给出了(8192, 3, 6)码在基于两种滑窗长度设置方法的JCED算法下的BER性能曲线。作为对比，同时给出了图1所示(1024, 3, 6)码的BER性能曲线。由图中可知，在不同码长下基于交叉熵滑窗长度设置方法和基于DFT滑窗长度设置方法的JCED算法有着几乎相同的BER性能；(8192, 3,6)码在BER= 10−5时，JCED算法与理想估计条件下的BP译码算法相比仅有不足0.1 dB的性能差距，而与仅已知局部噪声方差的均值的BP译码算法相比可获得1.4 dB的性能增益。与(1024, 3, 6)码的结果对比可知，在给定的BER下，相同码率的LDPC码，码长越长，JCED算法与理想估计条件下BP译码算法的性能差距越小，与仅已知局部噪声方差的均值的BP译码算法相比性能增益也越大，但总体而言两者随码长变化的趋势不明显。

图6 相同码率，不同码长的码在所提JCED算法下的BER性能

图7 相同码长，不同码率的码在所提JCED算法下的BER性能

3.2.2 不同码率LDPC码的仿真

图7给出了码率分别为 1/4 和3 /4的(1024, 3,4)码和(1024, 3, 12)码在基于两种滑窗长度设置方法的JCED算法下的BER性能曲线，再结合图1所示(1024, 3, 6)码的BER性能曲线，可以看到：在不同码率下，基于两种滑窗长度设置方法的JCED算法有着几乎相同的BER性能；(1024, 3, 4)码、(1024, 3, 6)码和(1024, 3, 12)码在BER= 10−5时，JCED算法与理想估计条件下的BP译码算法相比均只有0.15～0.25 dB的性能差距，而与仅已知局部噪声方差的均值的BP译码算法相比可分别获得2.4 dB, 1.2 dB和0.4 dB的性能增益。因此，JCED算法相对于仅已知局部噪声方差均值的BP译码算法的性能增益随码率变化的趋势非常明显，JCED算法更适合提升中低码率的码在非平稳信道下的BER性能。

3.2.3 规则与非规则LDPC码的仿真

图8给出了码长、码率均相同的(2048,3,6)规则码与CCSDS标准中的AR4JA非规则码在基于两种滑窗长度设置方法的JCED算法下的BER性能曲线。由图中可知，无论对于规则码还是非规则码，基于两种滑窗长度设置方法的JCED算法有着几乎相同的BER性能；在平稳信道下性能优异的非规则码，在非平稳信道下依然保持着对规则码的性能优势；非规则码在BER= 10−5时，JCED算法与理想估计条件下的BP译码算法相比均只有0.2 dB的性能差距，而与仅已知局部噪声方差的均值的BP译码算法相比可获得1.5 dB的性能增益，规则码也有相同的结论。因此，JCED算法对规则码与非规则码同样适用，没有明显的性能倾向。

图9给出了CCSDS标准中的AR4JA非规则码在基于两种滑窗长度设置方法的JCED算法下的错误平层验证曲线。错误平层产生的原因有两种，可能是码结构本身造成的，也可能是译码算法或译码算法的实现细节造成的。该码具有良好的最小距离特性，且在平稳信道下已通过官方FPGA平台验证在BER= 10−8下不存在错误平层，因此排除了码结构本身导致错误平层的可能，能够用来检验JCED算法是否会导致错误平层。由图中可知，在BER=10−8下，基于两种滑窗长度设置方法的JCED算法均不会导致错误平层。

图8 相同码长的规则与非规则码在所提JCED算法下的BER性能

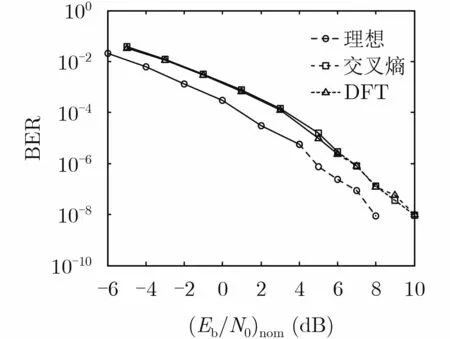
图9 所提JCED算法的错误平层验证

4 结束语

为解决非平稳信道下的高效信道估计与译码问题，提出一种基于SWBP的JCED算法。同时分别基于交叉熵和DFT提出两种低复杂度的自适应滑窗长度设置方法。计算复杂度分析和仿真结果表明，基于两种滑窗设置方法的JCED算法有着几乎相同的接近最优的BER性能，在BER= 10−5时与理想信道估计下的BP译码算法仅有0.25 dB以内的性能差距，但基于DFT滑窗设置方法的JCED算法有最低的计算复杂度，其单轮迭代计算复杂度仅比BP译码算法高22%。同时，所提JCED算法对局部噪声方差初始估计值不敏感，即使信噪比失配达±6 dB也不会影响BER性能，算法有很强的鲁棒性。对不同码长，不同码率，规则与非规则码的大量仿真结果表明，在非平稳信道条件下，所提JCED算法对所考察的码的BER性能提升均有效，特别是对中低码率的码。另外，通过仿真验证了所提JCED算法在BER=1 0−8时不会导致错误平层。