不同斜溜槽倾角下矿石对井壁撞击力影响的实验研究

杨建东，张治强,2，路增祥,2，段文硕

(1.辽宁科技大学矿业工程学院，辽宁 鞍山 114051；2.辽宁省金属矿产资源绿色开采工程研究中心，辽宁 鞍山 114051)

溜井是矿山低成本、高效率运输矿石的主要通道之一，其作用极为重要。但是从斜溜槽进入溜井的矿石会对井壁产生撞击，造成井壁变形、失稳、垮塌等问题，针对这些问题许多专家学者进行了研究，如路增祥等[1]系统总结了溜井研究现状以及当前存在的各种问题，认为矿石对井壁的冲击、剪切等是井壁变形破坏的根本原因；任智刚等[2]用全站仪记录了岩石层变化情况，研究了不同地质结构下矿石对井壁的撞击分布点以及破坏规律；王平[3]、秦秀山[4]通过三维激光扫描技术对溜井垮塌区域进行探测，分析了井壁垮塌的原因，并提出相应的加固措施。

在矿山实际工程中，溜井的破坏主要有断面扩大、支护结构破坏、围岩偏帮和垮塌等[1,5]，造成这种破坏的主要原因是进入溜井的矿石有各种各样的棱角，在下移的过程中，对井壁产生频繁的撞击、磨损和剪切作用，导致井壁逐渐被破坏，严重时出现大面积垮塌。一旦溜井发生破坏，不仅修复困难还危及工作人员生命安全，严重影响矿山的正常生产[6]。为了避免矿石垂直下落时对贮矿仓内物料的夯实，矿山一般采用斜溜槽将矿石卸入溜井。由于斜溜槽与溜井之间存在一定的角度，使得入井后的矿石在法线方向(水平方向)有分速度，因此矿石在溜井内下落时必然与井壁发生撞击[7]。矿石对井壁的撞击作用时间很短，撞击作用会很大，对井壁的破坏非常严重[8-9]。井壁的磨损或者破坏位置主要由矿石在溜井内的运移轨迹决定，同时还受矿石的粒度级配与形状、溜槽-溜井系统结构等因素的影响[10-11]。

矿石对井壁持续撞击作用是造成井壁变形、失稳和垮塌破坏的最直接最根本的原因[12]，因此，维护溜井应该从研究撞击力的大小和变化规律入手。明确撞击力的大小和作用时间，不仅能计算井壁破损体积[13]，还能确定撞击后矿石块的运移轨迹，以便有针对性的进行支护和加固。斜溜槽倾角不同，矿石进入溜井后的运移轨迹也不同，矿石对井壁的撞击力和撞击角度也随之发生变化。借助高速力值测量采集系统和实验室溜井模型，研究了不同斜溜槽倾角情况下撞击力大小、撞击接触时间以及它们的变化规律。

1 撞击位置与粒径的关系

矿石块沿斜溜槽下滑时，其下滑的高度、与斜溜槽的接触形式、摩擦因数以及自身的运动形式等都会影响其与井壁的撞击位置。假设矿石块是一个均质球状体，在斜溜槽上距O点的垂直距离为h的A点开始下滑，若不考虑矿石块与斜溜槽之间的摩擦力并将其看作质点，无论矿石块粒径如何变化，到达O点的速度均为V0，且入井后的运移轨迹呈二次抛物线[6]。在矿山实际中，进入溜井的矿石的粒径不尽相同，假设矿石块进入溜井前的运移轨迹不受粒径影响，理论上，粒径不同的矿石块在井壁上的撞击位置也不相同，粒径较大的矿石撞击位置相对较高，粒径较小时撞击位置相对较低，如图1所示。图1中，B点、C点为矿石与井壁的实际的撞击位置，B′点、C′点为理论上球心运移轨迹与井壁所在面的交点。受斜溜槽倾角θ的影响，矿石块与井壁撞击前瞬间，其速度方向与井壁之间存在夹角β，称为撞击角。当θ逐渐增大时，V0在法线方向的分量逐渐减小，切线方向的分量逐渐增加，导致图1中的B点、C点、B′点、C′点的位置逐渐向下移动。

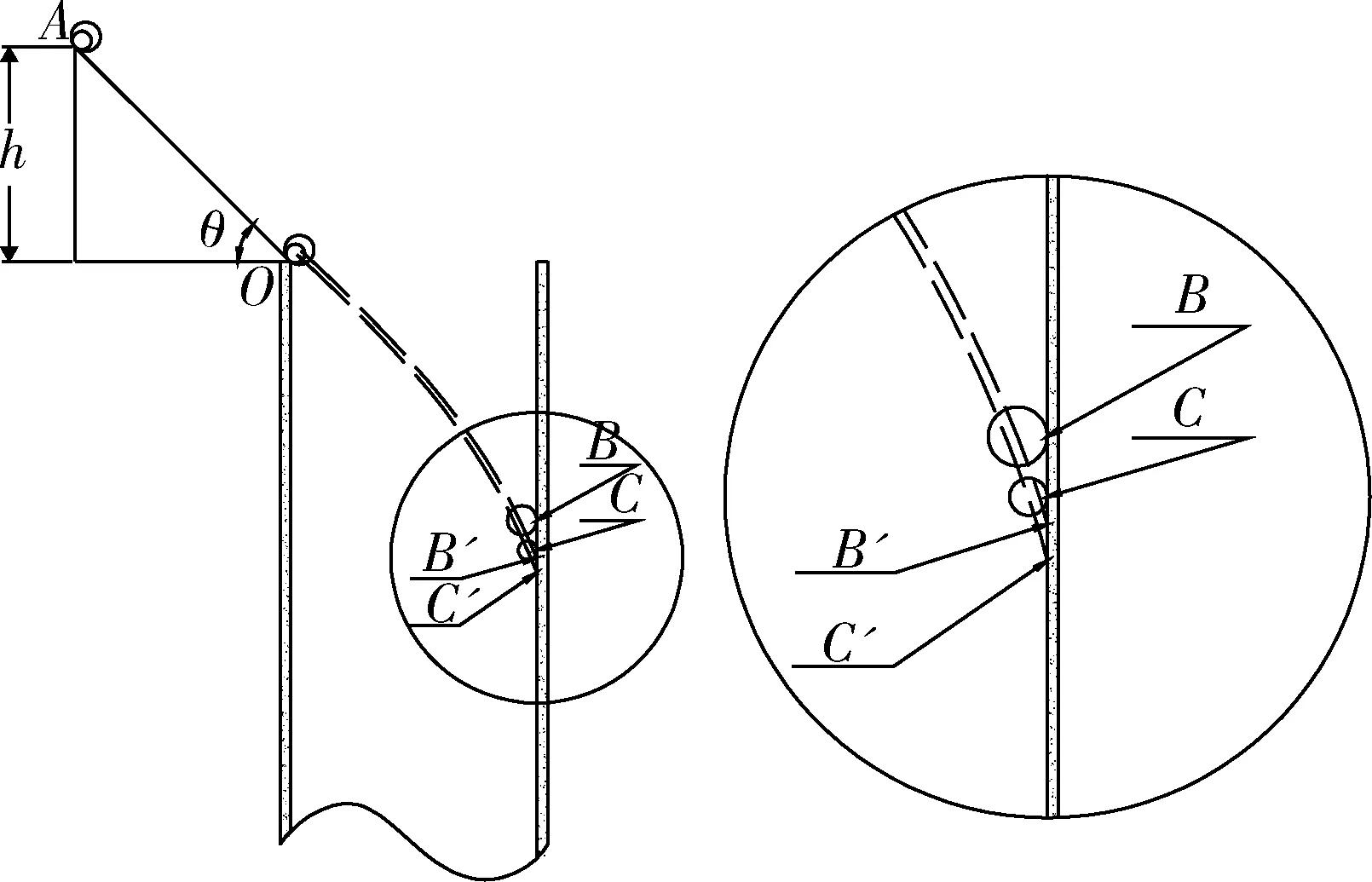
图1 撞击接触示意图Fig.1 Collision contact diagram

2 撞击力变化规律

2.1 实验室实验

实验室采用高度为2 000 mm、厚度为20 mm、外直径为500 mm的亚克力管制作溜井模型，亚克力管上口设计倾角可变的斜溜槽，模型示意图如图1所示，用角钢将传感器固定在模型内壁后，井筒的有效内直径为410 mm。为了使矿石在斜溜槽上只滑动，选取块状矿石[14]，其质量分别为29.6 g和70.5 g，测出矿石块的长、宽、厚，计算出其粒径分别为27.3 mm和37.2 mm。

针对矿石块下滑撞击，根据不同的斜溜槽倾角θ(45°、50°、55°、60°、65°)设计了五组实验方案，每一组方案均进行质量分别为29.6 g和70.5 g的两种矿石块实验，每一种实验均重复50次。实验中，将矿石块置于斜溜槽上A点，矿石块由静止从A点下滑，进入溜井后与安装在井壁的传感器发生撞击，传感器内部元件把撞击力值以电信号的形式传输到数据采集仪，经数据采集仪处理后再将撞击力值传输到电脑的数据显示软件，根据显示软件上的时间-力值的曲线图，能够准确记录每一次撞击的力值大小和撞击接触时间。

为了研究粒径对撞击力的影响，选择质量与矿石块相近钢球代替矿石块重复上述实验。钢球质量分别为32.7 g和71.5 g，对应的粒径为20 mm和26 mm。由于矿石块在下移过程中伴随有旋转、翻转等现象，导致与传感器的撞击点总会发生变化，故采取多次重复实验，并选择撞击点靠近传感器中心区域的30次实验数据(力值和接触时间)求其平均值，将平均值作为最终撞击点的力值。

2.2 法向力和切向力变化规律

矿石块对传感器的撞击力分解为沿井壁方向的切向力和垂直井壁方向的法向力，法向力的大小通过撞击力传感器测得，切向力大小计算见式(1)。

Fτ=Fncotβ

(1)

式中：Fτ为切向力；Fn为法向力；β为撞击角。

实验中，矿石块与井壁的撞击角大小计算见式(2)。

(2)

式中，R为井筒有效内半径。

撞击角的计算结果见表1。 由表1可知，斜溜槽倾角增大时，撞击角逐渐减小，说明倾角增大时，矿石速度的法向分量变小，切向分量增大，其运移轨迹也发生变化，导致矿石块与井壁的撞击位置向下移动。

表1 运移轨迹与井壁的夹角Table 1 Angle between migration trajectory and wall of a well

当斜溜槽倾角较小时，矿石块与井壁的撞击角较大，撞击过程中，井壁承受的法向撞击力相对较大，切向撞击力相对较小，对井壁造成的破坏程度较大，破坏范围较小，表现为撞击造成的印痕较深较短；当斜溜槽的倾角逐渐增大时，撞击角逐渐减小，法向撞击力逐渐减小，切向撞击力逐渐增大，井壁的破坏程度逐渐减小，破坏范围逐渐增大，表现为撞击造成的印痕较浅较长，撞击力大小的变化趋势与切向力大小的变化趋势基本相同，这说明切向力在撞击过程中起主导作用，井壁的破坏形式主要表现为剪切破坏。不同溜槽倾角情况下法向力、切向力大小如图2所示。

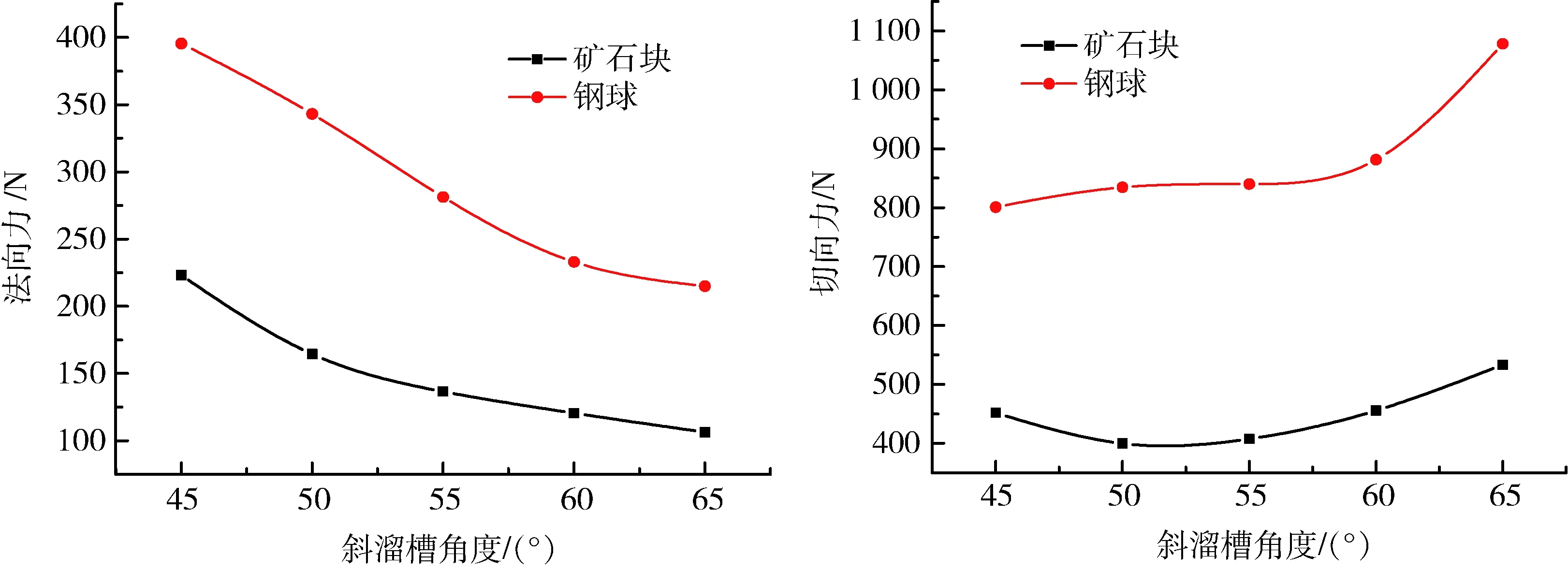
图2 法向力和切向力与斜溜槽倾角的关系Fig.2 Relation between normal force and tangential force and angle of chute

由图2可知，法向力随斜溜槽倾角的变化曲线近似于抛物线，设多项式为：Fn=aθ2+bθ+c，通过计算得到参数a、b和常数项c以及相关系数R2的值，见表2。

将拟合方程进行显著性检验，取显著性水平α=0.01，当n=5，m=2时，相关系数临界值为Rmin=0.990，R>Rmin，说明所建立方程与实验数据拟合很好。如钢球质量为71.7 g时，对应的二次多项式的方程见式(3)。

2.3 粒径对法向力和切向力的影响

由图2可知，当钢球和矿石块质量接近、斜溜槽角度相同时，作用于井壁的法向力与切向力变化趋势相同，但是矿石块撞击井壁产生的法向力和切向力均较钢球要小，主要原因是：①矿石块密度较小，质量相近时，矿石块的粒径较大，与井壁的撞击位置相对较高，矿石块与井壁撞击前的速度和钢球的速度相比较小，撞击前的动能也相对较小，使得撞击过程中井壁的变形较小；②由于材料自身的性质存在差异，导致矿石块与传感器撞击过程中的接触时间较大，钢球的接触时间较小，根据动量定理可知，矿石块的撞击力较小；③从斜溜槽下滑时，钢球与斜溜槽的接触近似于点接触，矿石块属于面接触，在质量相近时，钢球受到的摩擦力较小，矿石块受到的摩擦力较大，使得矿石块的实际入井速度V0相对钢球较小，撞击前的速度也较小。

3 接触时间变化规律

矿石块或者钢球与传感器接触后，在撞击力作用下，传感器产生变形，测得的力值逐渐增大。当撞击力值达到最大时，传感器的变形量也达到最大，此后，矿石块或者钢球逐渐离开传感器，当完全离开传感器表面后，对传感器产生的作用力变为零，传感器的变形恢复，传感器力值显示为零，上述变化过程如图3所示。因每一次撞击的接触点均存在差异，接触时长不尽相同，分析时取30次实验的接触时间的平均值。

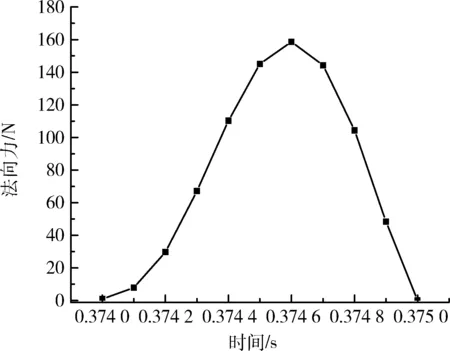
图3 法向力随时间的变化关系Fig.3 Relationship between normal force and time

撞击接触时间与两个撞击物体的变形程度和材料性质有关，变形越大，撞击接触时间相对越长。图4显示了质量相近的钢球和矿石块的撞击接触时间与斜溜槽倾角之间的变化关系。由图4可知，随着斜溜槽倾角的增大，钢球与传感器撞击接触时间均小于相近质量块石块与传感器撞击接触时间，无论矿石块还是钢球，当斜溜槽倾角逐渐增大时，其与传感器的撞击时间均逐渐减小。

图4 接触时间与斜溜槽倾角之间的关系Fig.4 Relationship between contact time and chute angle

4 结 论

1) 当斜溜槽倾角较小时，矿石块与井壁的撞击角较大，井壁承受的法向撞击力相对较大，切向撞击力相对较小，对井壁造成的破坏程度较大，破坏范围较小；当斜溜槽的倾角逐渐增大时，撞击角逐渐减小，法向撞击力逐渐减小，切向撞击力逐渐增大，井壁破坏程度逐渐减小，破坏范围逐渐增大，并且撞击力大小的变化趋势与切向力大小的变化趋势基本相同。

2) 当钢球和矿石块质量接近、斜溜槽角度相同时，作用于井壁的法向力与切向力变化趋势相同，但是矿石块对井壁撞击产生的法向力和切向力均较钢球要小。

3) 斜溜槽倾角在45°～65°范围时，质量相近的矿石块和钢球与传感器的撞击接触时间不同，钢球与传感器的撞击接触时间相对较短。