基于数值模拟的锚杆锚固缺陷检测研究

董佳琦，刘怡明，林 童，王润垚，孙晓云

(1.石家庄铁道大学电气与电子工程学院，河北 石家庄 050043；2.苏州大学机电工程学院，江苏 苏州 215137)

随着工程建设的快速发展，作为主要承重与支护结构的锚杆锚固支护系统被广泛使用，因此，对锚杆锚固系统健康状态的检测越来越重要。传统的检测方法主要是拉拔试验和取芯法，两种方法都具有一定的破坏性，且速度慢、效率低，仅能进行少量抽样检测来判断整体情况。基于磁致伸缩原理的超声导波技术作为一种新的超声导波无损检测方法，具有快速、便捷、长距离等检测特点，是无损检测领域的新研究方向。但基于磁致伸缩导波的锚杆锚固检测研究相对较少，尤其是在锚固损伤判断方面，有待进一步发展。工程中在役锚杆健康状态及质量检测使用磁致伸缩导波进行检测，具有重要的研究价值和应用前景。

磁致伸缩导波检测主要利用磁致伸缩效应及逆效应，最初由KAULE[1]提出基于磁致伸缩导波无损检测技术，并将其应用到钢索损伤检测中，但效果并不理想。CHASE[2]、KWUN等[3]应用磁致伸缩导波技术对含缺陷钢筋和管道进行了研究性实验，为缺陷无损检测提供了基础。李隆涛等[4]、何存富等[5]、刘增华等[6]、焦敬品等[7]通过研究不同类型和参数的磁致缩换能器设置，利用有限元仿真实现了在管道中激励出纵向导波和扭转导波。武新军等[8]、丁秀莉等[9]应用磁致伸缩导波解决了带包覆层管道的缺陷检测问题。龙盛蓉等[10]、李志农等[11]利用有限元仿真软件COMSOL对磁致伸缩导波的产生、传播和接收进行了相关的模拟。何文等[12-15]应用有限元瞬态动力响应方法，对超声导波在水泥砂浆锚固中的传播进行研究，实现低频纵向导波和扭转导波在锚杆有效长度和锚固密实度检测，并与实验结果较好吻合，此外也研究确定了导波检测锚杆脱锚缺陷的最优激发频率。赵宇亮等[16]、廖霖等[17]、马洁腾等[18]、张昌锁等[19]、赵宇亮[20]结合数值分析和实验，对低频和高频纵向导波在锚杆锚固检测中的应用进行了研究，主要探讨注浆质量、有效锚固长度、锚固系统内导波传播规律等关键问题。牛海萍[21-22]采用在未锚固端和岩体表面安装传感器的方法，用超声导波对锚固质量进行判断。

本文使用COMSOL有限元仿真软件搭建锚杆锚固模型，确定了最佳激励频率，对影响检测效果的偏置磁场参数进行了分析，确定了较优的磁路和磁铁个数，主要分析了锚杆或锚固的有效长度、锚杆或锚固缺陷的大小对反射波波形的影响程度，并且参考模型数据搭建实验检测平台，验证了电磁超声技术应用于锚杆锚固检测中的可行性和优势。

1 原 理

电磁超声换能器(electromagnetic acoustic transducer，EMAT)主要由线圈、磁铁和待测构件组成，是用于锚杆检测的基本结构(图1)。检测过程中，信号的激发基于磁致伸缩效应，首先给激励线圈施加交流信号，线圈感应出交变磁场，处于交变磁场中的铁磁性材料随磁场变化产生机械振动，此振动本质是应力波，在试件中经过复杂的反射、折射等，以导波的形式传播出去。接收过程基于磁致伸缩的逆效应，由试件上振动导致空间磁场的变化，接收线圈在变化磁场作用下，产生感应电压，最后由接收到电信号来对试件进行质量诊断。

图1 磁致伸缩换能器结构图Fig.1 Structure diagram of magnetostrictive transducer

1.1 激励线圈中的电磁场方程

导波的本质是由试件的应力-应变形成在波导内传播的弹性波，磁致伸缩导波的产生同样如此，波在弹性介质中的动力方程由力的平衡方程、几何方程及材料的物流方程构成[23]。所用激励信号激发的导波属于低频超声导波，换能器工作时激发频率在兆赫兹以下，能达到准静态近似条件的要求，故求解中可忽略位移电流所带来的影响。线圈的脉冲涡流动态磁场满足式(1)。

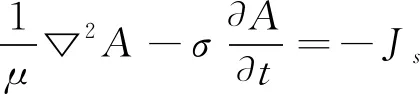
(1)

式中：A为矢量磁位；σ为铁磁体的电导率；Js为源电流密度；μ为铁磁体的磁导率。

磁致伸缩换能器与被测试件一般提离较小，本实验所用到的激发频率在20～100 kHz之间，要将交流线圈的趋肤效应等考虑在内，其源电流密度可表示为式(2)。

(2)

式中：i为交流线圈的总电流；S为线圈的截面积。

将式(2)代入式(1)可得到式(3)。

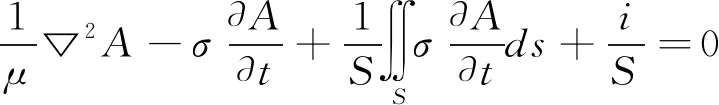
(3)

换能区域内的电场强度与矢量磁位之间满足式(4)。

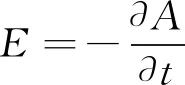
(4)

换能线圈以及被测试件的涡流密度可表示为式(5)。

(5)

1.2 频散曲线分析

频散曲线是研究导波的基础，一般可从中确定群速度和相速度，其对研究结果有重要影响。本实验钢材料的杨氏模量为280 GPa，泊松比为0.3，密度为7 500 kg/m3，利用PCDISP软件[24]求解自由锚杆纵向导波L(m,n)的群速度和频散曲线如图2所示，其中，m为环向位移，n为模态阶数顺序。由图2可知，小于150 kHz的区间仅有L(0,1)模态存在，有利于分析结果；高于150 kHz的区间出现了多模态，波形混杂，不利于分析结果。从图2还可以看出，L(0,1)模态在100 kHz内频散较小，有利于检测导波。因此，本文选用100 kHz以内的信号作为激励频率。

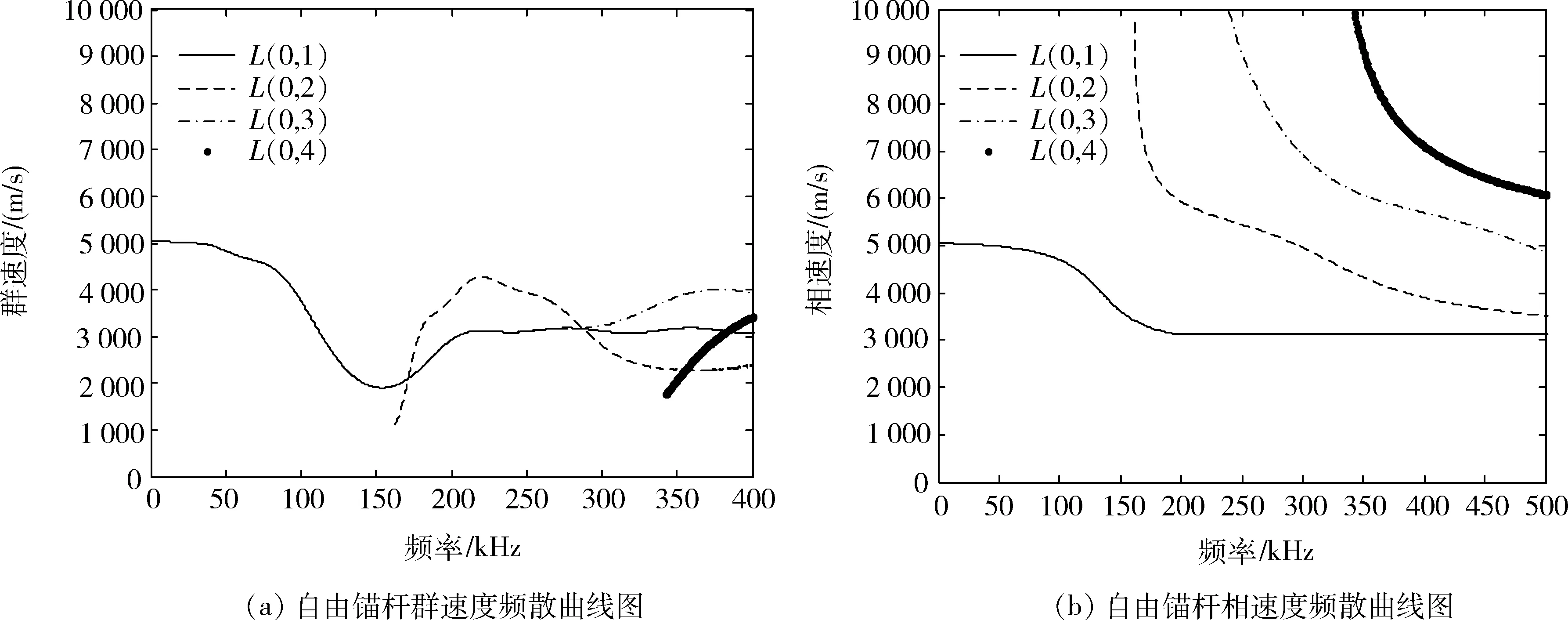
图2 频散曲线Fig.2 Dispersion curve

2 仿 真

2.1 锚杆模型建立

根据上述原理及公式运用Comsol Multiphysics软件对锚杆锚固体系进行建模与仿真计算，主要使用该软件中AC/DC模块与固体力学模块，并设置多物理场耦合实现电-磁-机械三个物理场间的转换，为避免干扰和减少计算量，设置了两个相隔的空气域，其结构如图3所示。 模型中，锚杆直径为20 mm，长为1 500 mm，激励线圈设置为150匝，接收为300匝，两线圈相距200 mm，永磁体设置剩余磁通密度0.4 T。激励信号采用经汉宁窗调制的正弦电流激励信号，其脉冲个数为4个、幅值为2 A、激励频率此处为50 kHz。考虑到精度和计算量问题，将锚杆网格划分设置为扫略，最大网格2 mm，最小网格0.2 mm；线圈和永磁体采用自由四面体网格，最大网格3 mm，最小网格1 mm；空气采用自由四面体网格，最大网格30 mm，最小网格3 mm。

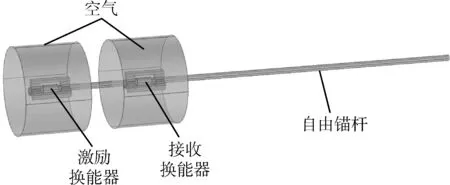
图3 锚杆三维建模图Fig.3 The 3D modeling drawing of anchor rod

2.2 偏置磁场参数选择

磁致伸缩导波检测中，偏置磁场起到了提高EMAT换能效率及消除超声导波倍频效应的作用，其参数的合理选择在一定程度上影响着检测结果。偏置磁场的提供方式一般为电磁铁或永磁体。本文的偏置磁场均由永磁铁提供，其单个尺寸设置为长30 mm，宽20 mm，高10 mm，每块设置的剩磁大小为0.4 T。

2.2.1 磁路对波形的影响

对于直径为20 mm的锚杆，选择的磁路个数一般为2～4个，换能器部分如图4所示，结构1表示换能器的偏置磁场为2磁路，结构2表示换能器的偏置磁场为3磁路，结构3表示换能器的偏置磁场为4磁路，此处激发与接收在磁路数量保持一致，对磁通密度分布与接收信号间关系进行分析。激发信号采用中心频率50 kHz的5周期调制信号。

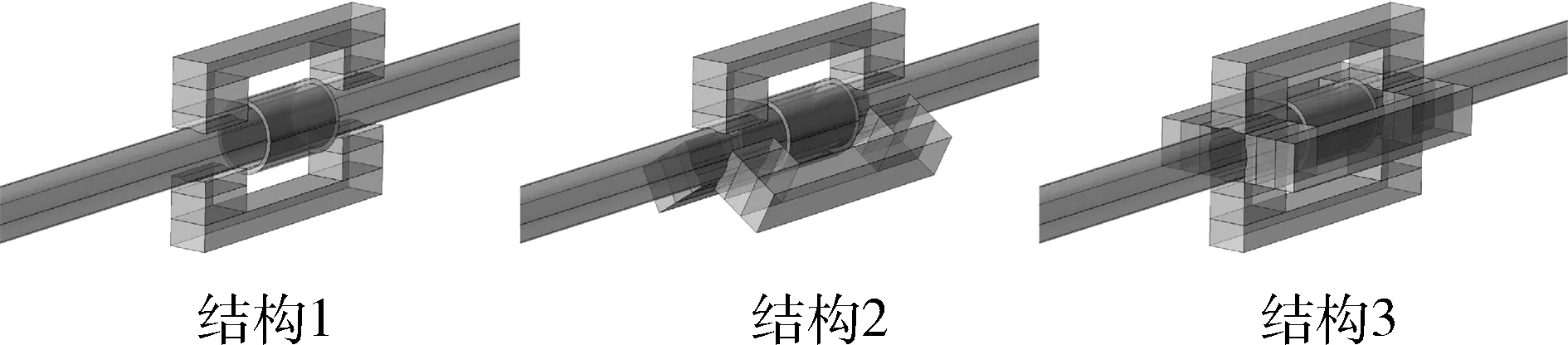
图4 三维换能器仿真模型Fig.4 The simulation model of three dimensional transducer

图5(a)为不同磁路下的磁场区域的分布情况。由图5可知，随着增加磁路的数量，磁通密度相应增大，其中，2磁路的磁通密度分布近似呈椭圆形，3磁路的磁通密度分布近似呈三角形，4磁路的磁通密度分布近似趋于圆形，同时相比于2磁路和3磁路，4磁路的磁通密度数值最大，其接收端接收到的信号会最强。各磁路下接收到的首波如图5(b)所示。由图5(b)可知，磁路数量的增加起到了提高信号幅值的作用，从2磁路增加到4磁路过程中，换能器的换能率明显提升，对波形幅值有较大改善，磁路在很大程度上影响了接收波形。考虑到锚杆截面尺寸，同时在实际实验中磁路越多设置操作越复杂，所以取3磁路为最优磁路个数。

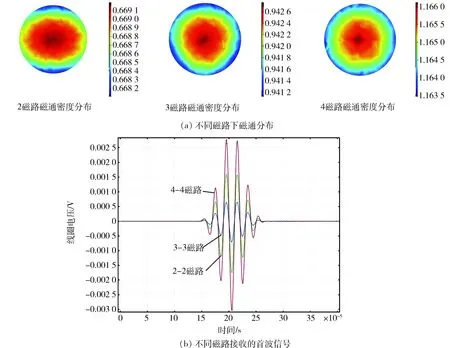
图5 不同磁路的磁通分布和首波信号图Fig.5 Flux distribution and first wave signal diagram of different magnetic circuit

2.2.2 永磁个数对波形的影响

根据磁致伸缩的材料特性，其磁特性曲线有一定的变化趋势，偏置磁场的大小存在最优空间，改变磁铁的个数将影响偏置磁场值的大小，从而影响换能效率，在3磁路情况下，改变磁铁数量，从1个增加至4个，通过轴线上的磁通密度分布情况观察磁铁个数所带来的影响，如图6(a)所示，接收到的首波波形如图6(b)所示。由图6(a)可知，磁铁数量的增加引起的磁铁密度变化逐渐放缓；由图6(b)可知，随着永磁数量的增加，磁通有增大趋势，但相比改变磁路数量带来的磁通密度改善较小，偏置磁场强度提升到一定幅值后将趋于平稳。考虑到实际操作中的设置问题，以及安装和拆卸换能器过程中的不安全因素，选择2～3个磁铁较为合适。

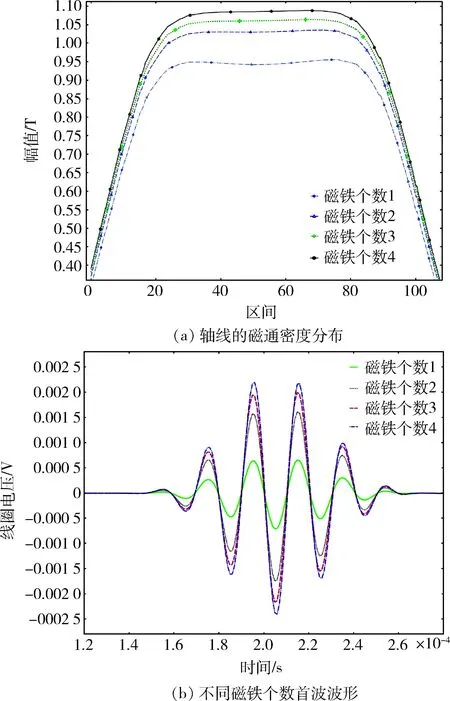
图6 不同磁铁个数的轴线磁通密度分布和首波信号图Fig.6 Axial flux density distribution and first wave signal diagram with different magnetic number

2.3 锚固模型建立

锚杆长为1 500 mm，其中，自由端设置长度为500 mm，锚固端长度为1 000 mm。 锚杆直径为20 mm，钻孔直径为50 mm，灌浆锚固厚度为10 mm，弹性模量为30 GPa，密度为2 700 kg/m3，泊松比为0.3，为了减少围岩干扰，锚固体直径应不低于62.7 mm[25]，锚固半径设置为390 mm，锚固和围岩材料的阻尼比设置为0.01。建立锚杆锚固系统模型后进行网格划分，考虑到仿真精确度和模型收敛性，将锚杆网格划分设定为扫略，最大网格1.5 mm，最小网格0.1 mm；线圈和永磁体采用自由四面体网格，最大网格2 mm，最小网格0.5 mm；空气域和围岩也采用自由四面体网格，最大网格20 mm，最小网格2 mm；灌浆设置和锚杆网格划分相同。

2.4 仿真结果分析

2.4.1 完整锚杆长度检测

采用时程曲线分析锚固的有效长度，该方法需要确定首波时间和反射波(底端或缺陷)时差△t，根据所测试件的波速C，得到接收与底端(或缺陷)之间距离L(L=C×Δt/2)。 分别对1.5 m、2 m和2.5 m的锚杆进行仿真实验，激励采用50 kHz的5周期调制信号激励。 设置示意图和导波传播示意图如图7(a)所示，反射波曲线如图7(b)所示。激励波经大约t1/2后到达接收端，称为首波，之后继续传播，t2/2后遇到底端面后向左传播，由于导波在自由锚杆中衰减较小，t2/2后又被接收端接收，称为底端面回波，根据回波和首波之间的时差Δt和波速C(为频散曲线计算出的50 kHz下自由锚杆波速4 901 m/s)，得到接收与底端(或缺陷)之间距离L。对1.5 m、2 m和2.5 m锚杆长度进行检测，结果见表1。由表1可知，锚杆实际长度与仿真计算的长度误差较小，磁致伸缩导波可用于自由完整锚杆检测工作。

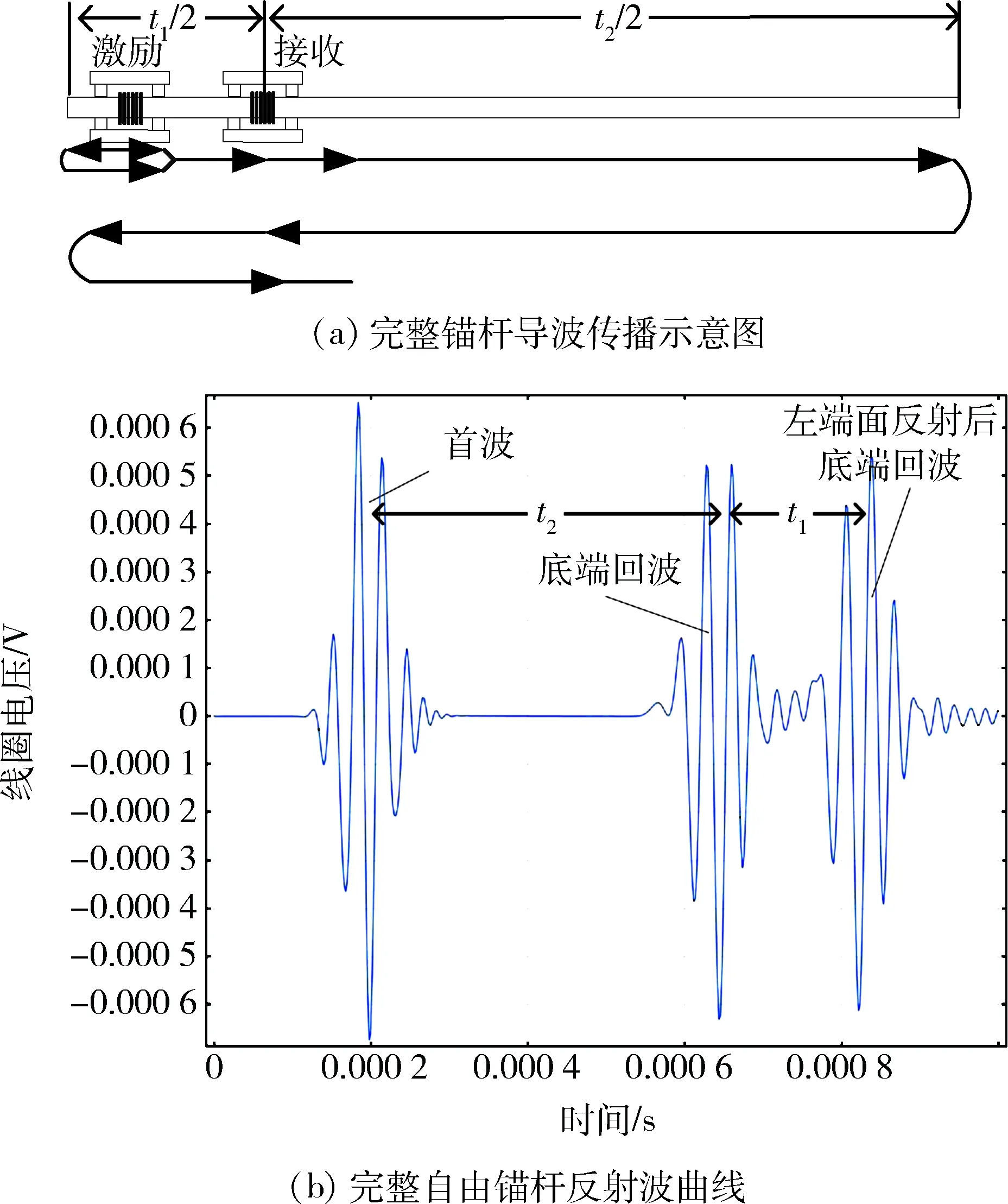
图7 完整锚杆导波传播示意图和反射波曲线图Fig.7 Schematic diagram of guided wave propagation and reflected wave curve of complete anchor rod

表1 完整锚杆长度的检测结果Table 1 The test results of complete bolt length

2.4.2 完整锚固长度检测

完整锚固的反射波曲线如图8所示，根据时程曲线得到锚固的长度。激励频率为50 kHz，锚固中波速为2 600 m/s，锚固长度为1 200 mm、1 500 mm的完整锚固长度的检测结果误差分别为2.5%、1.3%。电磁超声技术能有效检测锚固长度，但需注意的是，波遇到波阻抗界面将发生反射、透射，所以在存在锚固的情况下，波不断被反射、透射，衰减很快，这些后续波形会给波形分析带来困难，一般接收时程图仅分析锚固底端回波以前的信号波形。

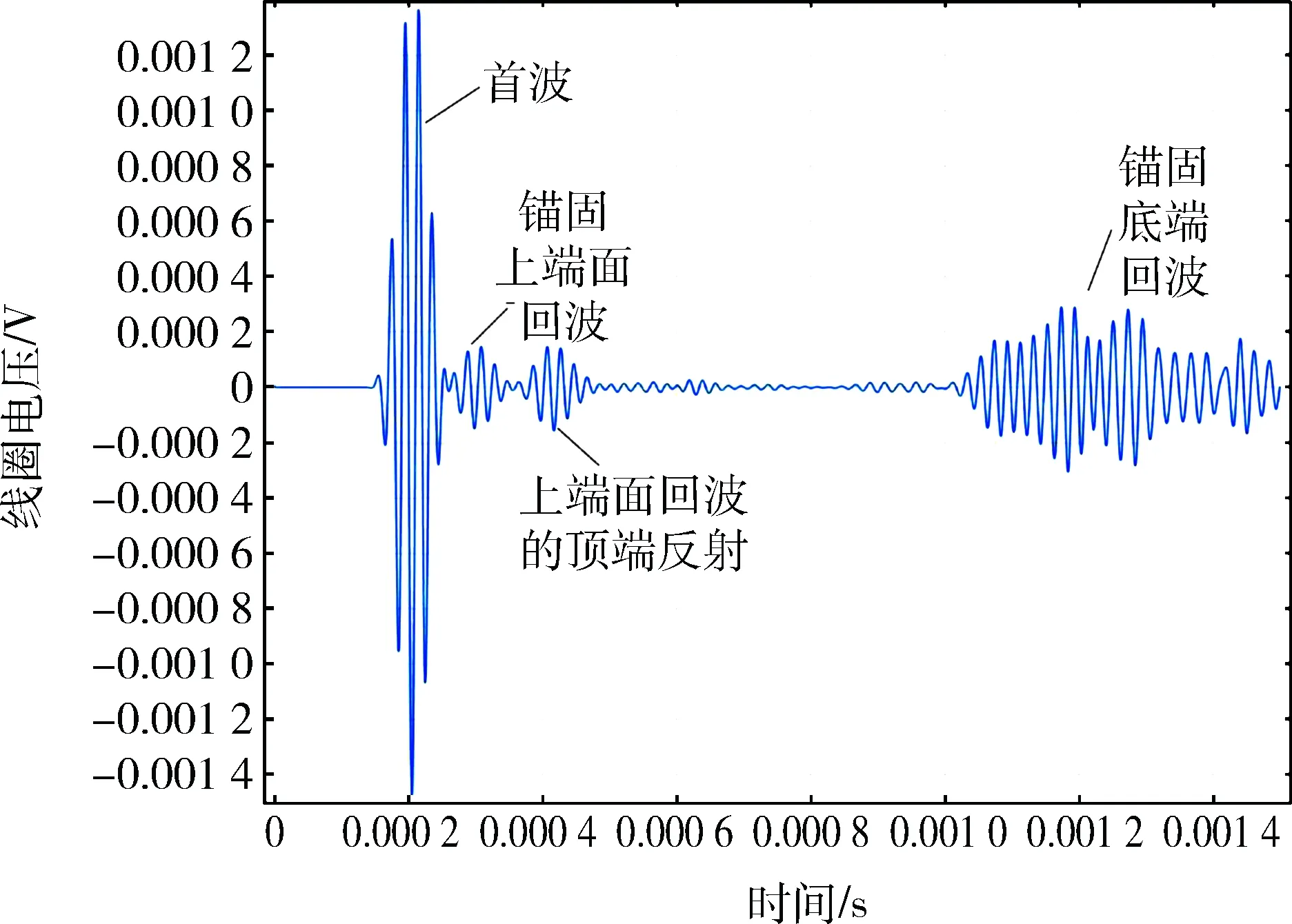
图8 锚固模型50 kHz激励下反射波曲线Fig.8 The reflected wave curve of anchorage model excited by 50 kHz

2.4.3 带缺陷自由锚杆检测

对长度为1.5 m的含缺陷自由锚杆进行质量检测的仿真计算，取距自由锚杆右端面700 mm位置处，缺陷初始设置为一个深度2 mm、长度10 mm的缺陷，仿真设置图和有限元模型，如图9(a)所示，反射波曲线如图9(b)所示，其中，波包2为缺陷反射信号，波包3为缺陷信号经左端面反射后的又一次接收，波包4、波包5分别为锚杆右端反射信号及右端信号又经左端面再次反射后的接收。

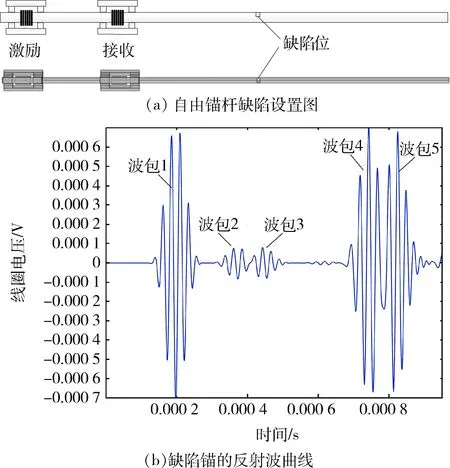
图9 自由锚杆缺陷设置和反射波曲线图Fig.9 Defect setting and reflected wave curve of free anchor

将缺陷深度以步长2 mm逐渐加深至10 mm，其反射波曲线如图10所示。由图10可知，当缺陷深度增加至10 mm时，即此时缺陷高度占锚杆直径的1/2，缺陷反射幅值已接近自由锚杆底端反射值。

图10 缺陷深度-反射波曲线Fig.10 The reflected wave curve of defect depth

以1.5 m长自由锚杆为例，设置的缺陷距右端面距离分别为1 000 mm、700 mm和300 mm。根据时程曲线可得到缺陷的位置。其中，激励频率为50 kHz，波速为4 901 m/s，其检测误差分别为1.49%、0.93%、1.16%。需要注意的是，对于靠近接收端或右端面的缺陷，当缺陷和它们之间距离小到一定程度时，波将发生混叠，不能区分出缺陷，所以换能器有一定的有效检测范围。

2.4.4 带缺陷锚固检测

不同尺寸的缺陷位置示意图如图11所示。激励频率为50 kHz，缺陷大小为15～80 mm，其仿真结果如图12所示。根据时程曲线，计算出缺陷距锚固上端面0.492 m，误差为1.6%。

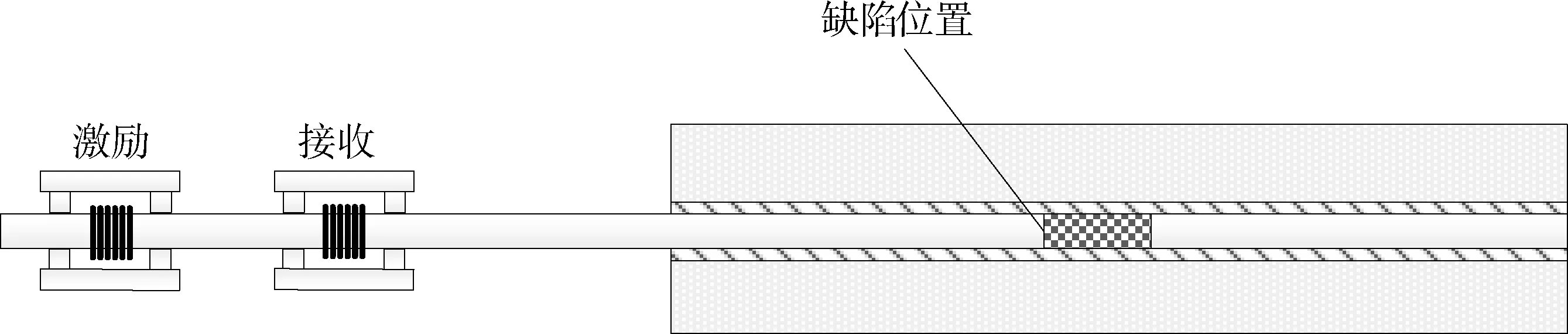
图11 缺陷位置设置图Fig.11 The setting diagram of bolt defect

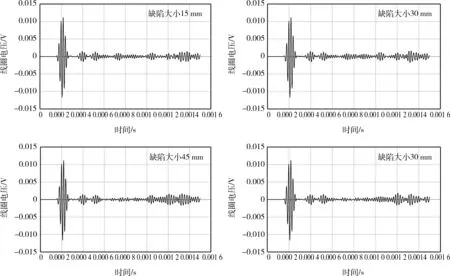
图12 不同尺寸缺陷时反射波曲线Fig.12 The reflected wave curve of different size defects

3 实验检测

实验室现有的锚杆长度为1.5 m，将磁致伸缩换能器激励端中心置于左端面0.15 m处，接收端中心置于左端面0.45 m处。采用任意波形发生器发射激励信号，设置频率为50 kHz，幅值为10 mV的5周期正弦脉冲信号；在波形发生器和激励换能器之间选用AE Techron公司的7224功率放大器，其具有噪声低、转换速率快、设计可靠等优点；信号采集部分使用东华测试公司的动态信号测试分析系统，其能够对接收端产生的电压信号进行采集和分析。通过施加50 kHz激励信号对带有缺陷的锚固进行检测，所采集到的信号如图13所示。由图13可知，第二个波包即缺陷的时刻为10.272 18 s，第三个波包时刻即右端面为10.272 42 s，计算得到的缺陷距右端面距离为0.585 m，与设置的位置0.6 m相比，误差为2.5%，可以看出误差较小，准确性较高。

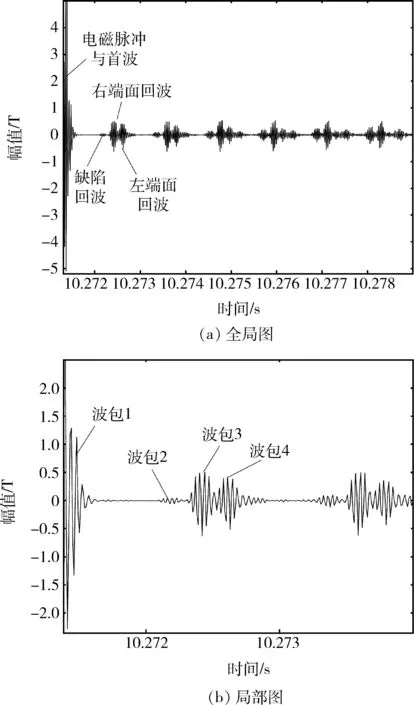
图13 带有缺陷的锚固反射波曲线Fig.13 The reflected wave curve of anchorage with defects

通过锚杆锚固中的实验验证，可以看到检测误差与实际设置相差不大，实验的结论与仿真能够比较好的对应，说明了磁致伸缩导波在锚固质量检测中的可行性。

4 结 语

本文搭建了锚杆锚固三维有限元模型，确定了最佳激励频率，对影响检测效果的偏置磁场参数进行了分析，确定了较优的磁路和磁铁个数，主要分析了锚杆或锚固的有效长度、锚杆或锚固缺陷的大小对反射波波形的影响程度，并且参考模型数据搭建实验检测平台，验证了仿真模型的可行性和准确性，且电磁超声技术应用于锚杆锚固检测中的可行性。