波形钢腹板连续刚构桥剪力滞效应的翼缘有效宽度法研究

熊绍伟,吴国松,冉志红,宋红旭,张 静,隆 凯

(1.云南大学 建筑与规划学院，云南 昆明 650500；2.重庆交通大学 工程设计有限公司，重庆 400074)

0 引言

波形钢腹板预应力组合箱梁桥20世纪80年代起源于法国，此后，该桥型在日本得到很大发展[1]。2005年，我国第一座波形钢腹板组合梁桥——江苏省淮安市长征桥(人行桥)建成以后，国内关于波形钢腹板预应力混凝土桥的研究和应用逐渐兴起。近几年，该桥型逐步往大跨径方向发展[2]。

与传统的预应力箱梁桥一样，波形钢腹板预应力组合箱梁桥在受力过程中同样会出现“剪力滞”现象。目前，相关的研究成果大多集中于剪力滞效应的解析解、影响因素以及一般分布规律等[3-7]，对剪力滞效应的翼缘有效宽度法研究成果较少。此外，以往的成果主要是针对中、小跨径的简支梁和连续梁桥，对跨越能力更强的连续刚构桥研究也较少。

《波形钢腹板组合桥技术标准》(CJJ/T272-2017)[8]推荐该桥型的剪力滞效应翼缘有效宽度法可以采用现行的《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 3362-2018)[9](以下简称2018版桥规)中的方法。

2018版桥规中剪力滞效应的翼缘有效宽度法是针对简支梁、连续梁和悬臂梁的。单看上部梁体，连续刚构桥悬臂施工时的受力模式和悬臂梁是相似的，成桥后的受力模式与连续梁同样是相似的。但是，2018版桥规中剪力滞效应的翼缘有效宽度法能否直接应用到波形钢腹板连续刚构桥上是值得研究的。

本文将以一座悬臂施工的波形钢腹板预应力连续刚构桥为例，通过建立杆系有限元模型和实体有限元模型，就2018版桥规中剪力滞效应翼缘有效宽度法对于大跨径波形钢腹板预应力连续刚构桥在悬臂施工阶段和成桥阶段的适用性进行研究。

1 工程背景

某座波形钢腹板预应力混凝土连续刚构桥，跨径布置为83 m+150 m+83 m，桥跨立面如图1所示。箱梁顶板宽12 m，底板宽6.5 m，单箱单室，直腹板，箱梁顶设置2%的单向坡。

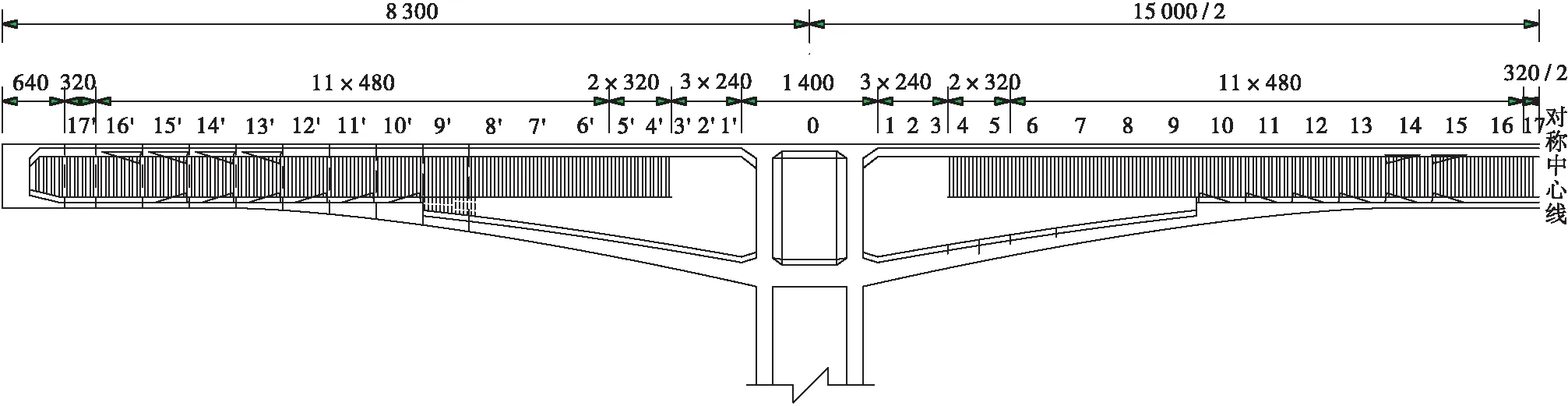
图1 桥跨立面(单位：cm)Figure 1 Vertical view of bridge(Unit:cm)

0号块根部梁高10 m，跨中合龙段至14#块以及边跨现浇段至14#块梁高4.5 m，其余梁段梁高按1.5次抛物线变化。10#块及10#块至13#块和13#块为底板加厚段，实现底板预应力钢束水平布置，消除曲线布置钢束造成的径向力，其余梁段的底板厚按1.5次抛物线变化。本桥除0号块外，还多出3个节段的混凝土梁段，此举不仅能留出空间锚固体内预应力，避免设置体外预应力，而且避免了在受力复杂区设置复杂结构，使结构更加安全可靠。为了保证波形钢腹板不发生剪切屈曲，4#、4#块至9#、9#块设置了外包混凝土和水平横隔板。图2为0号块根部截面，图3为过渡截面，图4为跨中截面。桥墩采用双薄壁墩，尺寸为6.5 m×1.7 m的矩形截面。

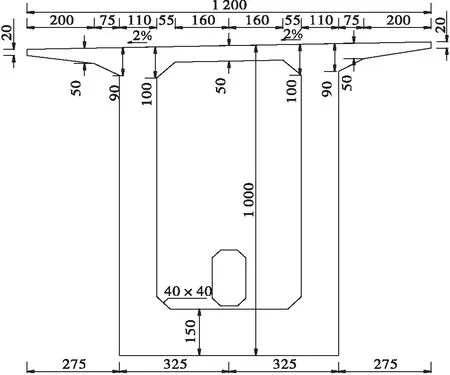
图2 根部截面(单位：cm)Figure 2 Root cross section(Unit:cm)

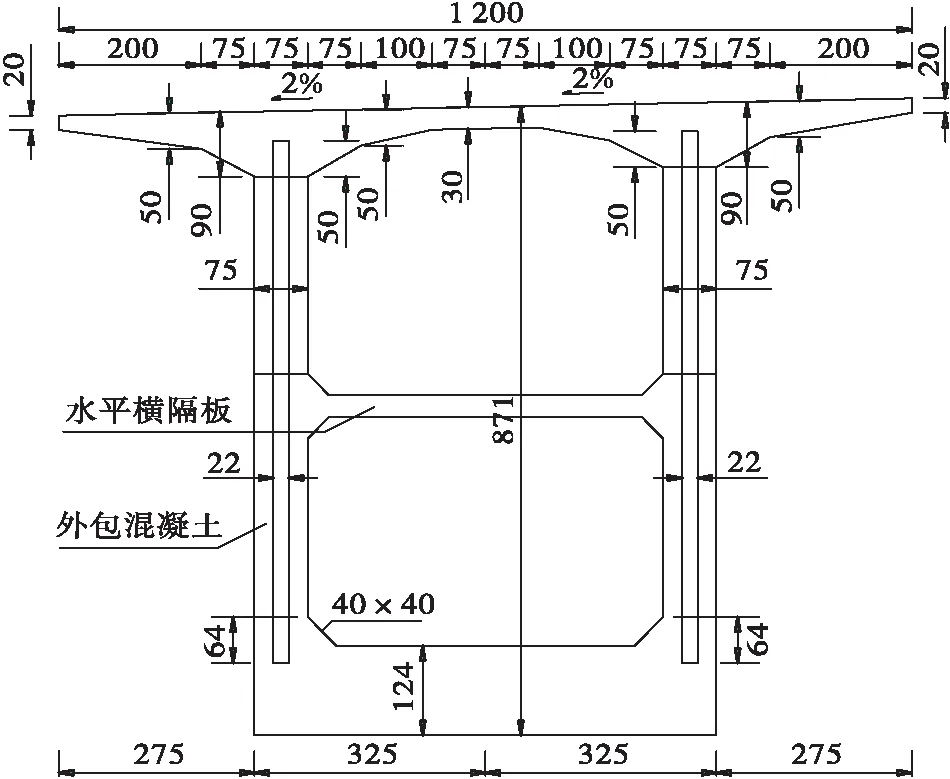
图3 过渡截面(单位：cm)Figure 3 Transition section(Unit:cm)

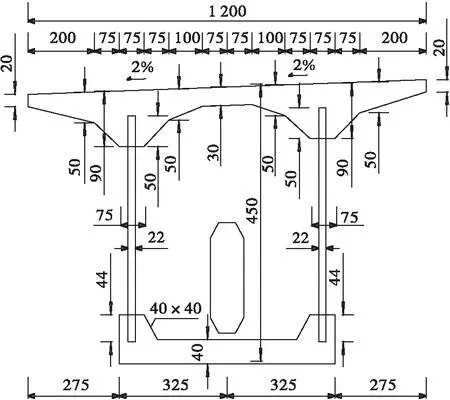
图4 跨中截面(单位：cm)Figure 4 Mid span section(Unit:cm)

上部箱梁采用C60混凝土，桥墩采用C50混凝土，钢板采用Q345qC钢，预应力束采用高强度、低松弛的预应力钢绞线。波形钢腹板与混凝土采用埋入式法连接，如图5所示，波形钢腹板采用1 600型，如图6所示。

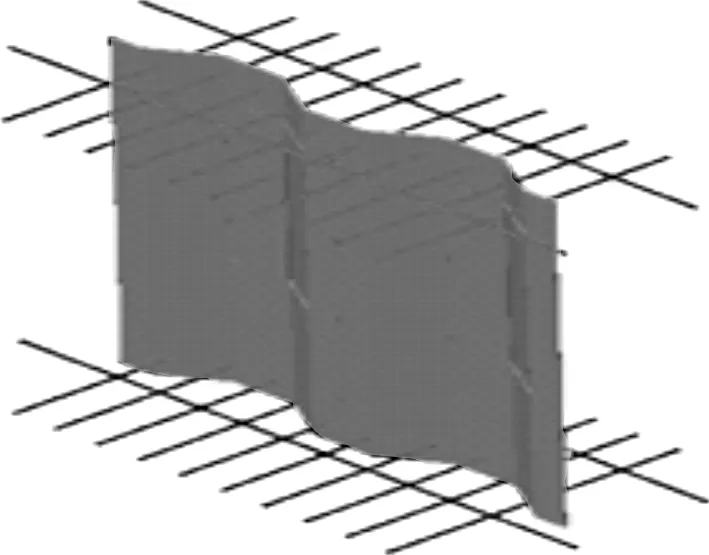
图5 埋入式连接(单位：cm)Figure 5 Embedded connection(Unit:cm)

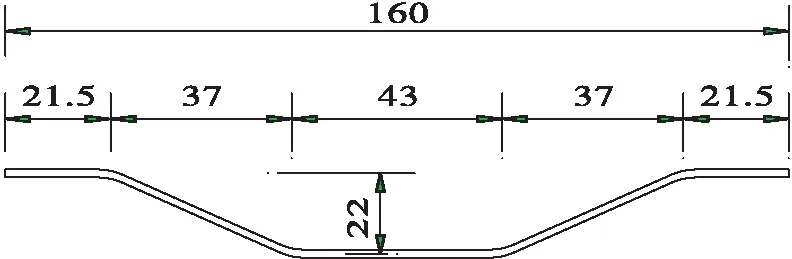
图6 1600型波形钢腹板(单位：cm)Figure 6 1600 corrugated steel web(Unit:cm)

边跨现浇段长6.4 m和0号块长14 m采用支架浇筑，边中跨合龙段长3.2 m段采用吊架浇筑，其余梁段采用挂篮悬臂浇筑。

2 分析方法

目前，关于剪力滞效应的研究方法常采用理论推导、有限元分析、模型梁实验等[10-14]。本文中初等梁理论下的正应力和实际正应力采用有限元计算。分析过程如下：

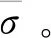
(1)

式中:σN为轴向应力，σM为弯曲应力。

b.用MIDAS FEA 建立实体有限元模型，得出考虑剪力滞效应后截面上的实际正应力分布及峰值应力σmax。

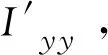
(2)

否则，

(3)

d.用c中的系数γ对(1)中的弯曲应力σM进行折减，得出剪力滞效应翼缘有效宽度法计算下的正应力σ，即:

σ=σN+γσM

(4)

e.将b中的σmax与d中的σ进行对比分析，依据分析结果对剪力滞效翼缘有效宽度法的适用性进行评价。

3 有限元模型

3.1 杆系有限元模型

杆系有限元模型采用MIDAS CIVIL建模，如图7所示，全桥共有117个节点，112个梁单元。

图7 杆系有限元模型Figure 7 Finite element model of bar system

3.2 实体有限元模型

实体有限元模型采用MIDAS FEA建模，为了节约存储空间和计算时间，实体模型沿纵向取1/2桥进行分析，如图8所示。全桥共有77 889个节点，256 436个单元，混凝土采用3D四面体单元，钢腹板采用2D四边形单元，局部如图9所示。

图8 实体有限元模型Figure 8 Solid finite element model

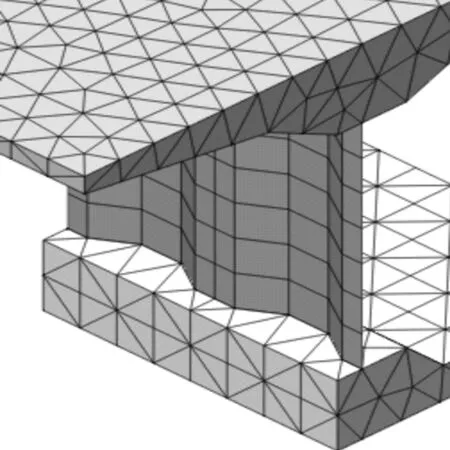
图9 实体模型局部Figure 9 Local representation of entity element model

混凝土顶、底板与波形钢腹板之间的连接假定为完全固结，通过共用节点法实现，这一假定的可靠性已在文献[6]和文献[15]中得到了验证。对于预应力钢束，MIDAS FEA中有对应的“植入式钢筋”功能进行模拟。

4 悬臂施工阶段分析

在悬臂施工过程中，悬臂段的长度是一个动态增长的过程。选取A-A和B-B两个截面，截面位置见图10，对这两个截面从7#块至16#块的施工过程进行分析。

4.1 悬臂梁翼缘有效宽度计算方法

2018版桥规中悬臂梁的翼缘有效宽度计算公式如下：

bmi=ρsbi

(5)

ρs=21.86(bi/li)4-38.01(bi/li)3+

24.57(bi/li)2-7.67(bi/li)+1.27

(6)

式中：bmi为腹板两侧上、下翼缘的有效宽度，i=1,2,3；bi为腹板两侧上、下翼缘的实际宽度，i=1,2,3；本文中bi为翼缘端至波形钢腹板中心的距离；ρs为悬臂梁悬臂段的有效宽度计算系数；li为理论跨径，对于悬臂梁li=1.5l，l为实际悬臂长度，本文中l为悬臂端至薄壁墩外侧的距离。

图10 计算截面位置(单位：cm)Figure 10 Calculating section position(Unit:cm)

4.2 分析结果

a.顶板分析结果。

A-A和B-B截面在施工过程中顶板实际正应力分布如图11所示，图中横向坐标的原点位于截面中心处。本文中应力值负号为压应力，正号为拉应力。在整个悬臂浇筑过程中，A-A和B-B截面的顶板正应力分布不均匀，应力峰值均出现在梁肋附近。

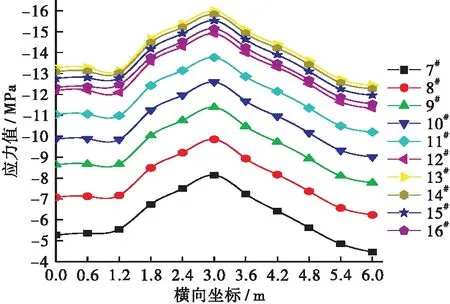
(a) A-A截面

(b) B-B截面

限于篇幅，翼缘的有效宽度和折减系数γ的详细计算过程以及MIDAS CIVIL计算的轴向应力σN、弯曲应力σM没有单独列出。

结合表1、表2和图12、图13可知，A-A截面从7#至9#，B-B截面从7#至11#修正应力值与实际应力值σmax比较接近。但是，当悬臂长度持续增长后，误差值越来越大，同一施工阶段A-A截面的误差大于B-B截面。在整个悬臂施工过程中，A-A截面的误差值介于3.59 %～11.53%；B-B截面的误差值介于0.19%～9.63%。

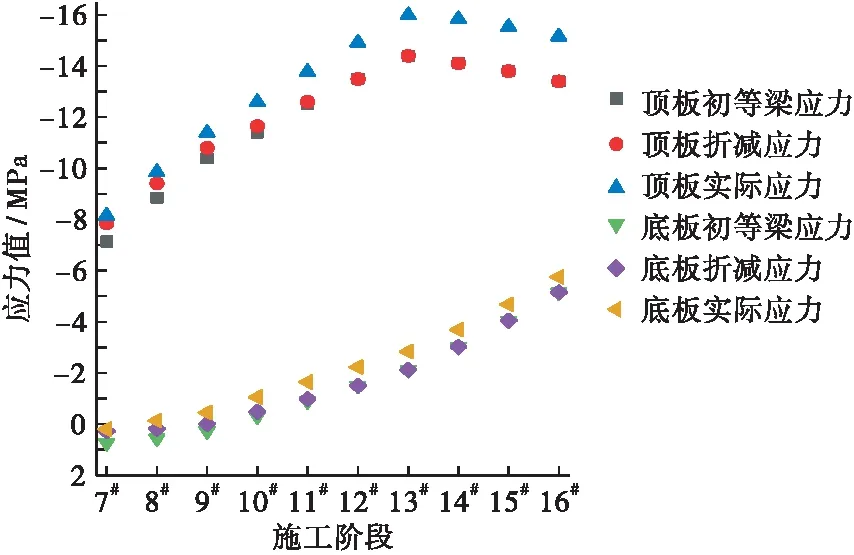
图12 A-A截面三项应力Figure 12 A-A section`s three normal stresses

b.底板分析结果。

A-A和B-B截面施工过程中底板实际正应力分布如图14所示，横向坐标的原点位于截面中心处。A-A截面底板正应力分布不均匀，峰值应力出现在梁肋附近。B-B截面底板正应力分布相对均匀，峰值应力位置靠近底板跨中位置。

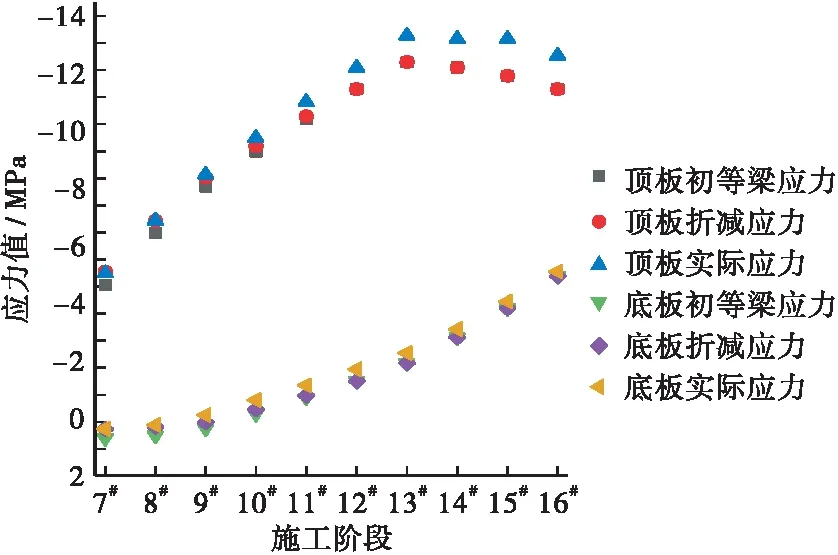
图13 B-B截面三项应力Figure 13 A-A section`s three normal stresses

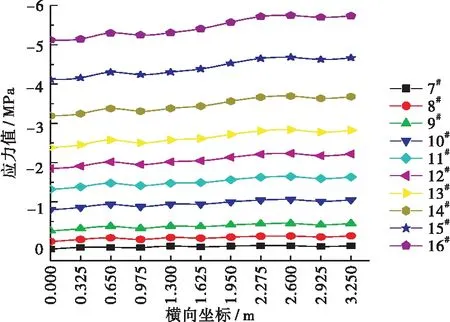
(a) A-A截面

(b) B-B截面

由图12、图13可知，2个截面在短悬臂阶段，底板初等梁应力和实际应力值较小，介于-2～0.7 MPa之间，而误差百分比有异常。2018版桥规规定，对于预应力结构，施工阶段的正应力允许范围为：-21.56～2.62 MPa。短悬臂状态下，底板正应力对结构的影响比较小，异常的误差百分比没有意义，本文不作具体分析。

从其余正常阶段的数据来看，随着悬臂长度增长，误差值逐渐减小；同一施工阶段，B-B截面的误差小于A-A截面。A-A截面的误差值介于10.36%～24.90%；B-B截面的误差值介于2.99 %～14.97%。悬臂施工阶段，剪力滞效应的翼缘有效宽度法对底板的适用性比顶板差。

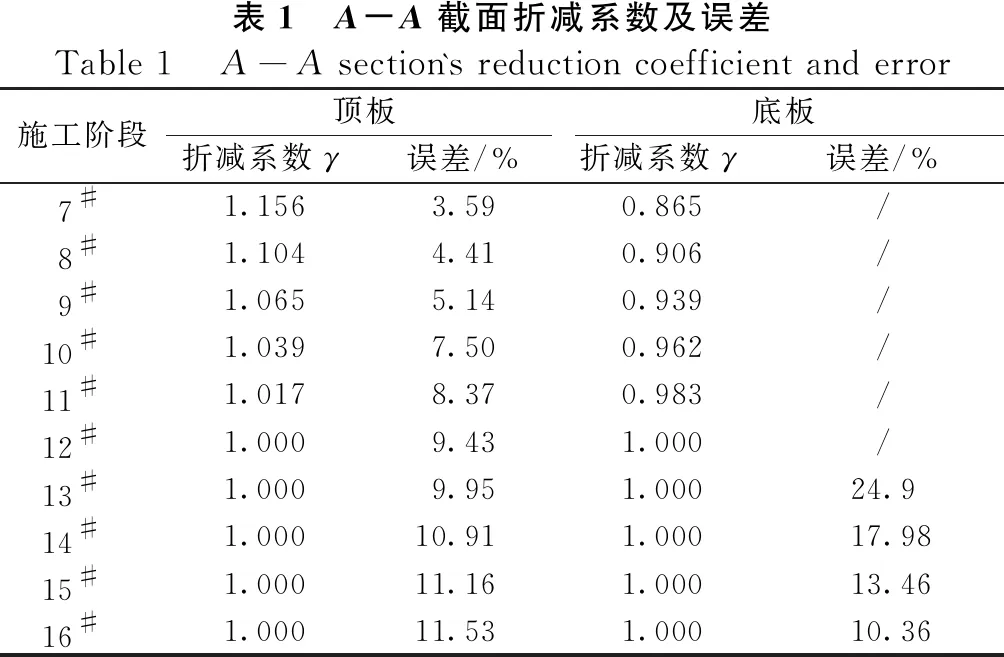
表1 A-A截面折减系数及误差Table 1 A-A section`s reduction coefficient and error施工阶段顶板底板折减系数γ误差/%折减系数γ误差/%7#1.1563.590.865/ 8#1.1044.410.906/ 9#1.0655.140.939/ 10#1.0397.500.962/ 11#1.0178.370.983/12#1.0009.431.000/13#1.0009.951.00024.914#1.00010.911.00017.9815#1.00011.161.00013.4616#1.00011.531.00010.36

表2 B-B截面折减系数及误差Table 2 B-B Section’s reduction coefficient and error施工阶段顶板底板折减系数γ误差/%折减系数γ误差/%7#1.1571.090.864/8#1.1040.190.906/9#1.0651.200.939/10#1.0392.960.962/11#1.0174.480.983/12#1.0006.041.000/13#1.0006.851.00014.9714#1.0007.511.0008.9815#1.0009.631.0005.5616#1.0009.161.0002.99

5 成桥阶段分析

边中跨合龙后，结构的体系发生改变，本文取桥面铺装完成后的阶段进行分析。除A-A、B-B截面外，再增加C-C、D-D、E-E、F-F4个截面进行分析，截面位置如图10所示。

5.1 连续梁中部梁段翼缘有效宽度计算方法

2018版桥规中连续梁中部梁段的翼缘有效宽度计算公式如下：

bmi=ρfbi

(7)

ρf=-6.44(bi/li)4+10.10(bi/li)3-

3.56(bi/li)2-1.44(bi/li)+1.08

(8)

式中：边跨梁段li=0.8l，l本文取边支座中心线与薄壁墩外侧间的距离；中跨梁段li=0.6l，l本文取两个主墩薄壁墩外侧间距离；ρf为连续梁中部梁段翼缘有效宽度计算系数；其余系数同上文。

5.2 分析结果

a.顶板分析结果。

成桥阶段所选取截面的顶板实际正应力分布如图15所示。

根部四个截面A-A～D-D以及边跨截面F-F的顶板正应力分布不均匀，峰值应力出现在梁肋附近；中跨跨中截面E-E的峰值应力出现在顶板端部。结合表3和图16，除F-F截面的误差值为15.91%外，其余截面的误差值介于3.90%～7.67%之间。对于顶板，成桥阶段剪力滞效应翼缘有效宽度法的适用性优于悬臂施工时的长悬臂状态，比短悬臂状态略差。

b.底板分析结果。

成桥阶段所选取截面的底板正应力分布如图15所示。截面A-A、C-C、E-E的底板正应力分布不均匀，截面B-B、D-D、E-E的底板正应力分布相对均匀。结合表3和图16，根部的4个截面A-A～D-D的误差较大，误差值介于9.67%～14.7%，E-E和F-F截面的误差相对较小，误差值分别为7.35%和5.64%。

(a) 顶板

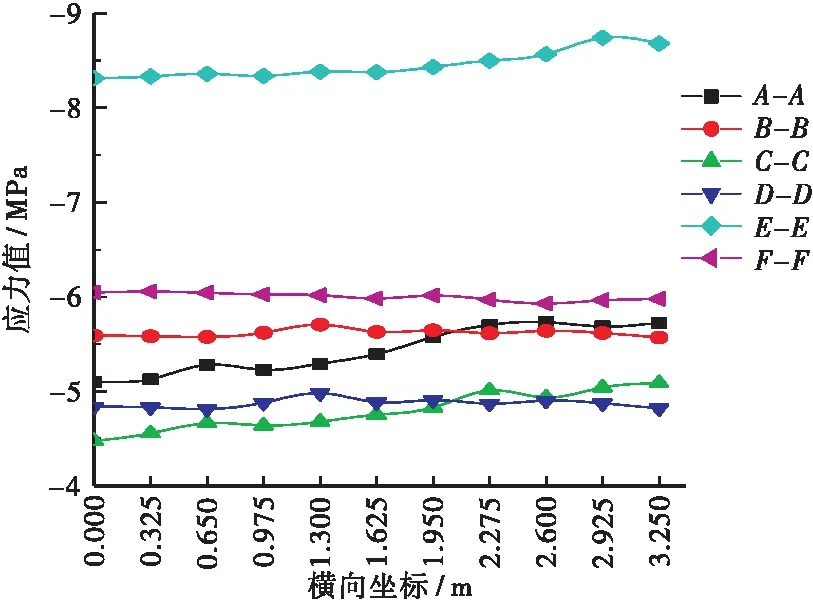
(b) 底板

图16 成桥阶段三项正应力Figure 16 Three normal stresses in the completion stage

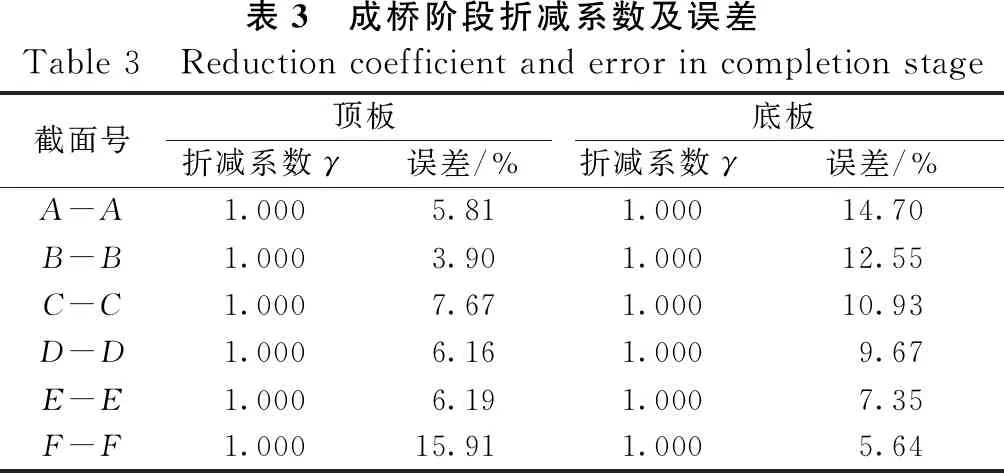
表3 成桥阶段折减系数及误差Table 3 Reduction coefficient and error in completion stage截面号顶板底板折减系数γ误差/%折减系数γ误差/%A-A1.0005.811.00014.70 B-B1.0003.901.00012.55 C-C1.0007.671.00010.93 D-D1.0006.161.0009.67 E-E1.0006.191.0007.35 F-F1.00015.911.0005.64

对于底板，成桥阶段剪力滞效应翼缘有效宽度法的适用性比顶板差，但是总体上比悬臂施工阶段好。

6 适用性分析

从表1～表3中的误差统计结果可以看出，误差值大于5%的截面是很多的。从3个表中的数据看，很多截面的折减系数γ取1是造成误差值较大的直接原因，而折减系数γ取1是因为翼缘有效宽度系数γ趋于1或大于1导致的。实际上，翼缘有效宽度不可能比实际宽度大，即有效宽度系数是不能比1大的。目前规范没有对此作出说明，本文的处理是对于大于1的情况按1考虑。

令悬臂梁的有效宽度系数ρs=1，相应的一个实根近似解为bi/li=0.04，因ρs和bi/li是单调递减的关系，即bi/li≤0.04时，不进行折减。同理，对于连续梁，bi/li≤0.05时，不进行折减。事实上，对于单箱单室的公路桥而言，翼缘实际长度bi一般在3 m左右，连续刚构桥主跨跨径l在100～200 m之间是常用跨径，bi/li≤0.04和0.05的情况是常见的。所以，对于2018版桥规中关于悬臂梁的剪力滞效应翼缘有效宽度法，当bi/li≤0.04时，不适用于悬臂施工时的波形钢腹板连续刚构桥；对于2018版桥规中关于连续梁的剪力滞效应翼缘有效宽度法，当bi/li≤0.05时，不适用于成桥后的波形钢腹板连续刚构桥。

7 结论

对于悬臂施工的预应力波形钢腹板箱形截面连续刚构桥而言：

a.悬臂施工阶段，2018版桥规中关于悬臂梁的剪力滞效应翼缘有效宽度法，随着悬臂长度的增加，顶板的适用性降低，底板反之；顶板的适用性优于底板；在整个悬臂施工过程中，顶板的误差值介于0.19%～11.53%之间，底板的误差值介于2.99%～24.90%之间。

b.成桥阶段，2018版桥规中关于连续梁的剪力滞效应翼缘有效宽度法，顶板的适用性优于底板，顶板的误差值介于3.9%～15.91%之间，底板的误差值介于5.64%～14.7%之间。

c.整体上看，2018版桥规中剪力滞效应翼缘有效宽度法的适用性，成桥阶段优于悬臂施工阶段。

d.对于2018版桥规中关于悬臂梁的剪力滞效应翼缘有效宽度法，当bi/li≤0.04时，不适用于悬臂施工阶段的剪力滞效应计算；对于2018版桥规中关于连续梁的剪力滞效应翼缘有效宽度法，当bi/li≤0.05时，不适用于成桥阶段的剪力滞效应计算。