高振荡积分计算的新型Clenshaw-Curtis-Filon 方法

郭 博 夏金键 曹 铭 吴清华

（湖南科技学院 理学院，湖南 永州 425199）

在工程应用领域经常涉及如下形式的高振荡积分计算问题

若有驻点，则直接转化后的 F(t)将出现奇异性。为了克服这个困难，Xiang 等提出了分区间，利用同胚变换tr+1=g(x)-g(ξ)和插值的方法，其中ξ是驻点[1]。该方法的误差分析建议采用端点处的导数插值方法对函数进行插值如在端点处使用埃米特插值。但该方法的插值公式较复杂，有时计算效果不佳。为此Domínguez等提出了 Filon-Clenshaw-Curtis 方法[2]。该方法先直接利用变换将积分转化为式(2)类型，再将区间分成若干小区间，在包含奇异点小区间内采样阶梯网格进行计算。对于不含奇异点的区间，利用切比雪夫多项式逼近F(t)，再利用正交多项式的性质得出递推公式。但该方法需要选择奇异小区间的长度及阶梯网格的参数。除此之外，还有其他考虑存在驻点的计算方法，如基于Levin 方法，推导出含有驻点时的计算公式。但对于一般振荡因子的高振荡积分计算问题，由于振荡因子的一般性，仍有许多问题值得深入研究[3]。

本文将在已有研究的基础上，对于一般的 g(x)，先利用同胚变换积分，再利用 Filon-Clenshaw-Curtis方法的思想，对被积函数中非振荡的函数在Clenshaw-Curtis 点上插值，再利用递推公式进行计算，最后通过数值算例验证算法的有效性和精度。

1 一般振荡因子的新型Clenshaw-Curtis-Filon 方法

对于没有驻点的情形，直接利用变换转化为标准振荡因子的即可，下面考虑含有驻点的情形。

对于有驻点的情形，不妨假设ξ∈(a,b)为 g(x)的唯一驻点，且g'(ξ)=g''(ξ)=…=g(r)(ξ)=0， g(r+1)(ξ)≠0，首先利用同胚变换tr+1=g(x)-g(ξ)，将式(1)转化为如下形式的积分

2 数值算例

该算例是有1 阶驻点的情形，首先利用同胚变换转化为类似(4)式的情形，具体见式(11)，再利用递推关系式(9)进行计算。当N=16，w=103，104，105，106时，用新方法计算的近似值和绝对误差由表1 给出。

表1 当N=16时计算的近似值和绝对误差

表1 和表2 中的精确值是通过Mathematica 软件的高精度计算获得，从中可以看出算法的计算精度很高，效果较好，且具有随着w 的增大，计算效果越好的特点。对于固定的w，随着展开项数N 的增加，绝对误差逐渐减少，最终快速达到机器精度，计算效果如图1 所示。

图1 w=105时的计算绝对误差图

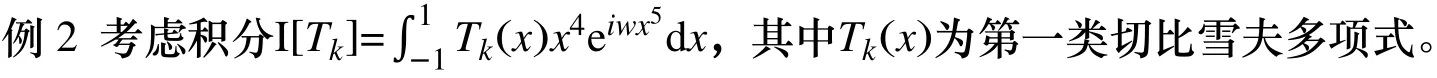
该算例是一个具有更高阶驻点的情形。当w=103时，对于0 到15 阶的切比雪夫多项式，用递推关系式(9)计算相应的高振荡积分，计算的近似值和绝对误差由表2 给出。

表2 当w=103时计算的近似值和绝对误差

从表2 可知，算法的计算精度较高，计算效果较好。

3 结 语

本文设计了一种新型Clenshaw-Curtis-Filon 方法，该方法能计算一般振荡因子的高振荡积分。数值实验验证了方法的有效性和计算精度。该方法成本低，便于实施，对高振荡积分的计算具有一定的价值。