基于Kriging模型的工程土方量计算方法分析

洪成晶

(中国路桥工程有限责任公司，北京100010)

土方量的计算是工程建设施工中重要的一环，直接关系到工程造价，是有效控制工程成本的重要依据[1]。目前土方量的计算方法主要由方格网法、等高线法、断面法以及DTM(数字地面模型)等，众多学者对这些方法进行了详细地研究，如常青[2]对上述四种方法的精度和适用性进行了研究分析，并用实例进行了证明；陈爱梅[3]等基于南方CASS软件平台对上述方法进行了对比分析，并提出了在使用过程中应注意的事项。

本文基于方格网法，针对方格网法的不足，减少外业的工作量，提出一种计算土方量的新方法，并通过具体案例进行分析验证，证明了本文方法的正确性和精确性。

1 方格网法概述

方格网法[4]是工程土方量计算的一种常用方法，其基本原理就是将待测区域划分为多个正方形网格，根据每个网格顶点的原地面高程和设计高程采用平均值法计算每个方形区域的填、挖方量，最后进行汇总，从而得到整个区域的填方和挖方的总量。基本的计算式如下：

(1)

式中:Hij为第i行第j列的方格网的高差；a、b为方格网的边长；n式待测区域的方格数量。

方格网法适用于大面积的土方量计算，尤其是地形变化较小，地势较为平坦的区域。对于地形起伏较大的区域，由于方格网法中假定同一网格线上高程同，最终土方量的计算精度会有所降低。因此在计算地形起伏较大区域的土方量时，往往需要对网格点进行加密，外业的工作量会随之大大增加，不利于工作效率的提高。

为了弥补方格网法的不足，将Kriging模型引入其中。其基本思路为：

(1)在待测区域均匀采集原地面的高程，获取一系列样本点。

(2)利用外业采集的样本点建立Kriging模型，实现对原地面地形的模拟。

(3)根据模拟的地形条件，采用方格网法划分网格并进行土方量的计算。

上述方法的优势在于在采用方格网法计算土方量时，网格顶点处的原地面高程可以由模拟出的地形直接给出，当网格需要加密时，不再需要进行外业测量，大大减少了工作量。

2 Kriging模型

2.1 Kriging模型基本原理

Kriging模型是1951年由南非工程师Krige提出的一种给予随机过程的无偏估计模型[5]，最早用于矿产储量分布的估计。在Giunta[6]、Sacks[7]等学者的推动下，Kriging模型目前已在气象、水文地质、地理信息系统、航空航天的多个领域获得广泛的应用。

Kriging模型是一种插值模型，在已知样本点x=[x1x2…xn]T和对应的n个函数响应值ys=[y1y2…yn]T的情况下，其插值结果由已知样本点的函数值线性加权得到，即：

(2)

因此，只要能给出加权系数ω=[ω1ω2…ωn]T，便可以估计出任一点处的函数响应。为此，Kriging模型引入统计学的假设，即将未知函数看作是某个高斯静态随机过程的具体体现。换言之，对于任意位置x，对应的函数响应y(x)被一个随机函数Y(x)代替，y(x)只是Y(x)可能的结果之一，即：

Y(x)=β0+Z(x)

(3)

式中：β0是未知常数，代表Y(x)的数学期望值；Z(·)是均值为0，方差为σ2的静态随机过程。

在设计空间中，不同未知处的随机变量之间的相关性可以用下式进行描述。

Cov[Z(x),Z(x′)]=σ2R(x,x′)

(4)

其中：R(x,x′)为相关函数，表示不同位置处随机变量之间的相关性。

为使Kriging模型预估值准确，要求下式所示的均方根误差：

(5)

最小，且满足无偏估计的条件。

引入拉格朗日方法，将上述问题转化为下式所示的求最小值问题：

minH(ω,λ)=σ2(1+ωTRω-2ωTrx)-λ(FTω-1)

s.t.FTω-1=0

(6)

式中：R为相关矩阵，由样本点之间的相关函数计算得到，R=(R(xi,xj))i,j∈n×n；rx为相关向量，计算方法为rx=[R(x1,x),R(x2,x),…,R(xn,x)]；F为n维单位列向量，F=[1 1 … 1]∈n。

对式(6)进行求解，可得：

λ=-2σ2(FTR-1F)-1(FTR-1rx-1)

(7)

ω=R-1(rx-F(FTR-1F)-1(FTR-1rx-1))

(8)

并将其带入到式(2)中，可以得到：

(9)

其中:β0可根据最大似然估计得到，其值为：

β0=(FTR-1F)-1FTR-1ys

(10)

2.2 相关函数

相关矩阵R和相关向量rx的建立都与相关函数的选取有关。目前许多学者采用高斯相关函数，主要由以下几类[8]：

(1)高斯函数：

Rk(xi,xj)=exp[-θk|xi-xj|2]

(11)

(2)各项同性高斯指数函数：

Rk(xi,xj)=exp[-θk|xi-xj|p] 1≤p≤2

(12)

(3)各向异性高斯指数函数：

Rk(xi,xj)=exp[-θk|xi-xj|pk] 1≤p≤2,k=1,2,3,…

(13)

式中:θ，p为相关函数参数。

3 土方量计算案例分析

3.1 案例选择

为对本文中提出的方法进行验证，假设有一方形场地，其尺寸为200m×200m，并且该场地内的地形满足式(14)所示的函数关系式。该方形场地的地形如图1所示。

(14)

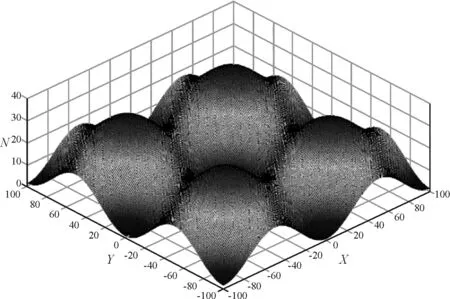
图1 原地面地形

从图1中可以看出，该场地内地形起伏较大，在四个波峰处(坐标分别为(-50,-50)、(-50,50)、(50,-50)、(50,50))原地面标高最大，为32.4m，在(0,0)处原地面标高最小，为0m。据此可以计算出该场地内最大平均坡度约为15°，若采用传统的方格网法进行土方量的计算，则需要对网格进行加密，工作量十分巨大。

3.2 均匀采样与地形模拟

为保证采样点能够均匀分布于场地之中，本文中采用均匀设计法来进行采样点的选取。均匀设计法是方开泰于1978年提出的[8]。首先产生均匀设计表，然后根据均匀性的度量标准如中心偏差、卷积偏差等来产生使用表，即最终的样本点。通过这一系列的过程，使样本点在设计空间内均匀分散。

图2为100个样本点的分布情况，从图中可以看出，样本点在场地内的分布十分均匀，满足均匀性的要求。

根据均匀设计获得的样本点之后，通过式(14)获取样本点处在该方形场地内的标高，然后采用Kriging模型对该场地的地形进行模拟，模拟出的地形如图3所示。在模拟过程中，各采样点之间的相关函数采用各向同性高斯指数函数，取θ=0.1，p=1。

图2 样本点均匀分布情况

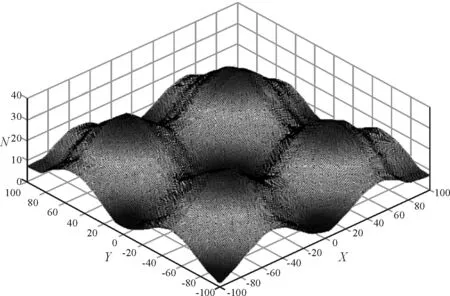
图3 Kriging模型拟合出的地形

对比图1和图3可以发现，Kriging模型能够较好地模拟出地形的起伏特点，模拟效果较好。

3.3 土方量计算结果分析

假设需要对该场地进行整平，整平后标高为15m。由于描述地形的函数已知，可以用积分方法算出填挖方的精确值。表1列出了本文中方法在不同采样点数量下的填挖方计算值。

从表中计算结果可以看出，随着样本点数量的增加，Kriging模型对地形的模拟越精确，最终填方量和挖方量的计算越准确，同时也标明本文中提出的方法的可行性与精确性。当样本点数量为120时，即样本点的平均间距为18.3m时，填方量和挖方量的计算误差均在5 %以内。

比较样本点的平均间距为20m时的计算结果，可以发现根据本文方法计算结果比传统方格网法的计算结果更加精确，与精确解相比，本文方法计算的填方量偏差为5.2 %，挖方量的计算偏差为2.7 %，而传统方格网法计算的填方量偏差和挖方量偏差分别为16.8 %和14.8 %，本文中方法的计算结果远远优于传统方格网法。从表中的数据可以发现，在相同的计算精度下，本文中方法所需的外业工作量远远小于传统方格网法。

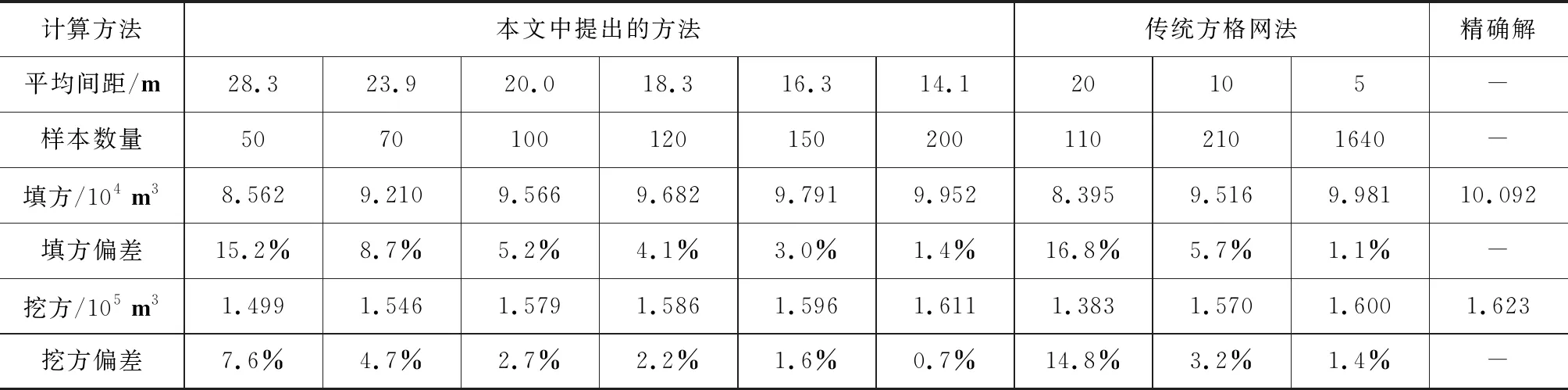
表1 不同样本数量下的计算结果对比

4 结论

本文基于方格网法，引入Kriging模型，提出了一种计算工程土方量的新方法，并用该方法对一起伏较大的地形进行了土方量的计算，主要结论如下：

(1)随着样本数量的增加，土方量的计算精度也就越高，在本文的算例中，当样本数量大于等于120时，与精确解相比，计算误差小于5 %。

(2)与传统的方格网法相比，本文中提出的方法计算精度更高，在相同的计算精度下，所需的外业工作量更少。