基于SPH-FEM耦合方法的泥石流冲击柱形结构物动力响应分析

韩俊辉， 姚昌荣， 余劲松， 匡 睿， 强 斌， 李亚东

(西南交通大学土木工程学院，四川成都 610031)

[通信作者]姚昌荣(1974～)，男，博士，副教授,主要从事桥梁防灾减灾、结构损伤识别及健康监测、桥梁施工控制研究工作。

泥石流是世界范围内常见的自然灾害，多发于山地、丘陵和高原地区[1]。我国正在修建的川藏铁路是继青藏铁路之后又一进藏铁路干线，将西藏纳入国家快速铁路网中，可加速西藏经济发展。川藏铁路地质条件复杂，沿线泥石流灾害频发，而川藏铁路桥梁占比高达13.2 %，桥梁面临的泥石流危害也不容小觑。

常用的泥石流研究方法有野外实测调查法、数值模拟法和水槽试验法等，其中数值模拟法以其较低的成本和研究上的便捷，逐渐成为研究泥石流广泛采用的方法。传统的泥石流数值模拟方法一般为基于网格的方法，但基于网格的方法在处理自由液面、大变形及多相流问题时有着难以捕捉自由液面、网格缠绕及网格需重新划分等不可避免的缺陷，近些年来，无网格方法越来越多的被用来模拟泥石流[2][4]。SPH方法作为无网格方法中较早提出且目前较为成熟的一种方法，越来越受到研究泥石流学者们的重视。

为分析不同横截面形式对泥石流冲击柱体动力响应的影响，本文以川藏铁路某泥石流沟的泥石流流变参数为例，采用非线性动力学数值模拟软件LS-DYNA，基于SPH方法建立泥石流浆体，FEM方法建立柱体，研究泥石流发生概率P分别为10 %、5 %、2 %和1 %条件下各不同截面柱体受泥石流冲击的动力响应。

1 SPH基础理论

1.1 SPH方法简介

SPH方法是一种基于粒子的纯拉格朗日方法，主要用来模拟连续介质。该方法克服了基于网格方法的难以捕捉自由液面、难以处理自由边界及物体发生大变形时网格缠绕等缺点，在模拟流体时具有基于网格方法不可比拟的优势[3]。

SPH方法最早于1977年由Gingold、Monaghan[5]和Lucy[6]提出用来解决天体物理问题，1992年Monaghan[7]首先将SPH方法拓展到不可压缩性自由表面流的模拟中。在计算流体领域中经过二十多年的发展，SPH方法在泥石流的模拟中已较为成熟。赵宏亮[8]采用Python语言基于SPH方法自编了模拟黏性泥石流运动过程的程序；Chen等[9]采用GIS建立的实际地形，基于SPH方法分析了在泥石流沟不同位置设置不同数量的拦挡坝对泥石流运动过程的影响；柳春等[10]采用SPH-FEM耦合的方法模拟了含大块石泥石流冲击拦挡坝的动力响应。

1.2 SPH方法的计算理论

SPH方法将计算域离散为携带物理属性的粒子，通过支持域内粒子核函数近似的形式求得某一粒子的物理属性[11](图1)。

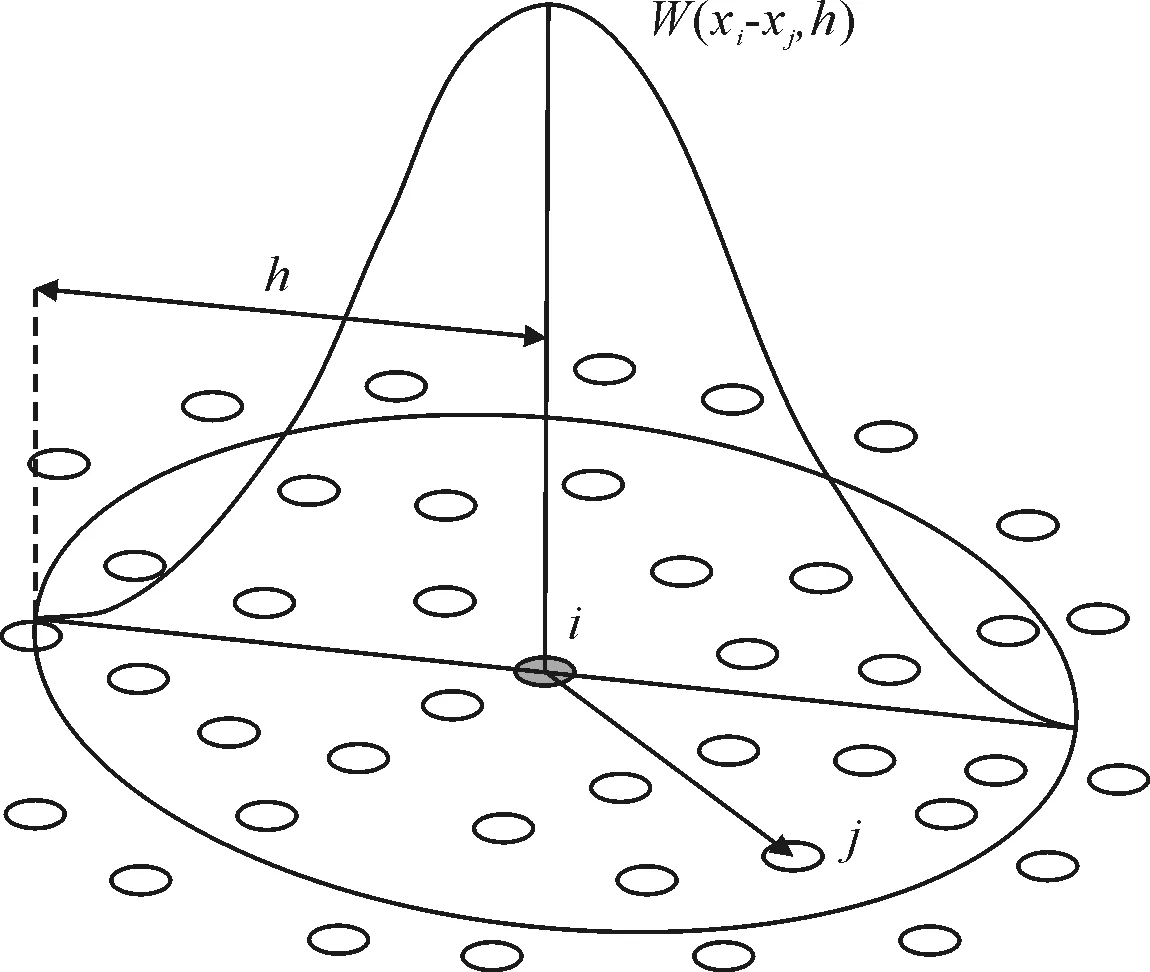
图1 粒子近似示意

(1)

式中：i和j分别代表粒子i和j；x为待求物理属性；N为粒子i支持域内的粒子总数；m为粒子的质量；ρ为粒子的密度；h为支持域半径，又称光滑半径；W(xi-xj,h)为核函数，又称光滑函数、权函数，形式如式(2)。

(2)

式中:d为所求问题的维数。

核函数形式有Bell-Shaped核函数、Gaussian核函数以及三次B-Spline核函数等，本文采用LS-DYNA中默认的三次B-Spline核函数，以θ(x)表示的形式为式(3)。

(3)

在离散的粒子框架下求解控制方程，流体控制方程Navier-Stoke方程的粒子近似形式为式(4)、式(5)[9]。

(4)

(5)

式中：t为时间；v为速度；α、β为坐标方向；p为压力；F为外力，如重力、摩擦力等。

2 建立模型

2.1 流变参数

根据中科院山地所的勘察报告，川藏铁路某泥石流沟泥石流为典型的暴雨型泥石流，其细颗粒黏粒含量较少，高频率条件下泥石流以稀性泥石流为主，低频率条件下则以过渡性泥石流或高容重低粘度的水石流为主。流变参数见表1。

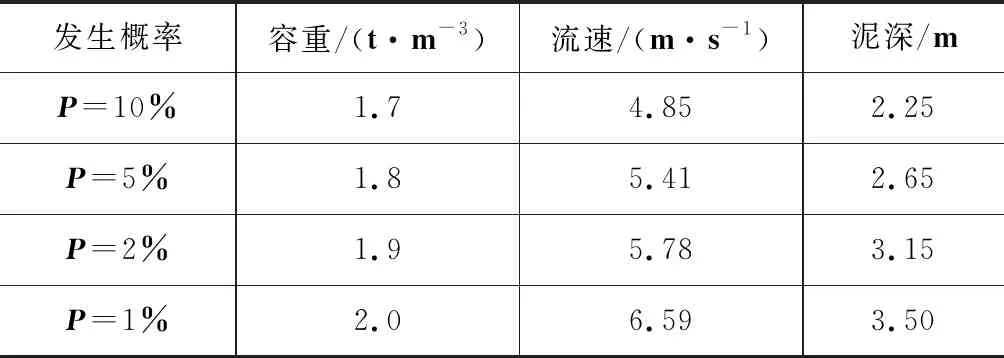
表1 泥石流流变参数

2.2 几何及网格模型

柱体高10m，采用实体单元建模，截面形状按TB10002-2017《铁路桥涵设计规范》[12]和JTGD60-2015《公路桥涵设计通用规范》[13]提供的流水压力计算的5种桥墩截面，分别为圆形、正方形、菱形、矩形和圆端形。柱体迎流宽度均设为1.5m，如图2所示。设置矩形和圆端形截面的目的是研究长宽比对冲击动力响应的影响。

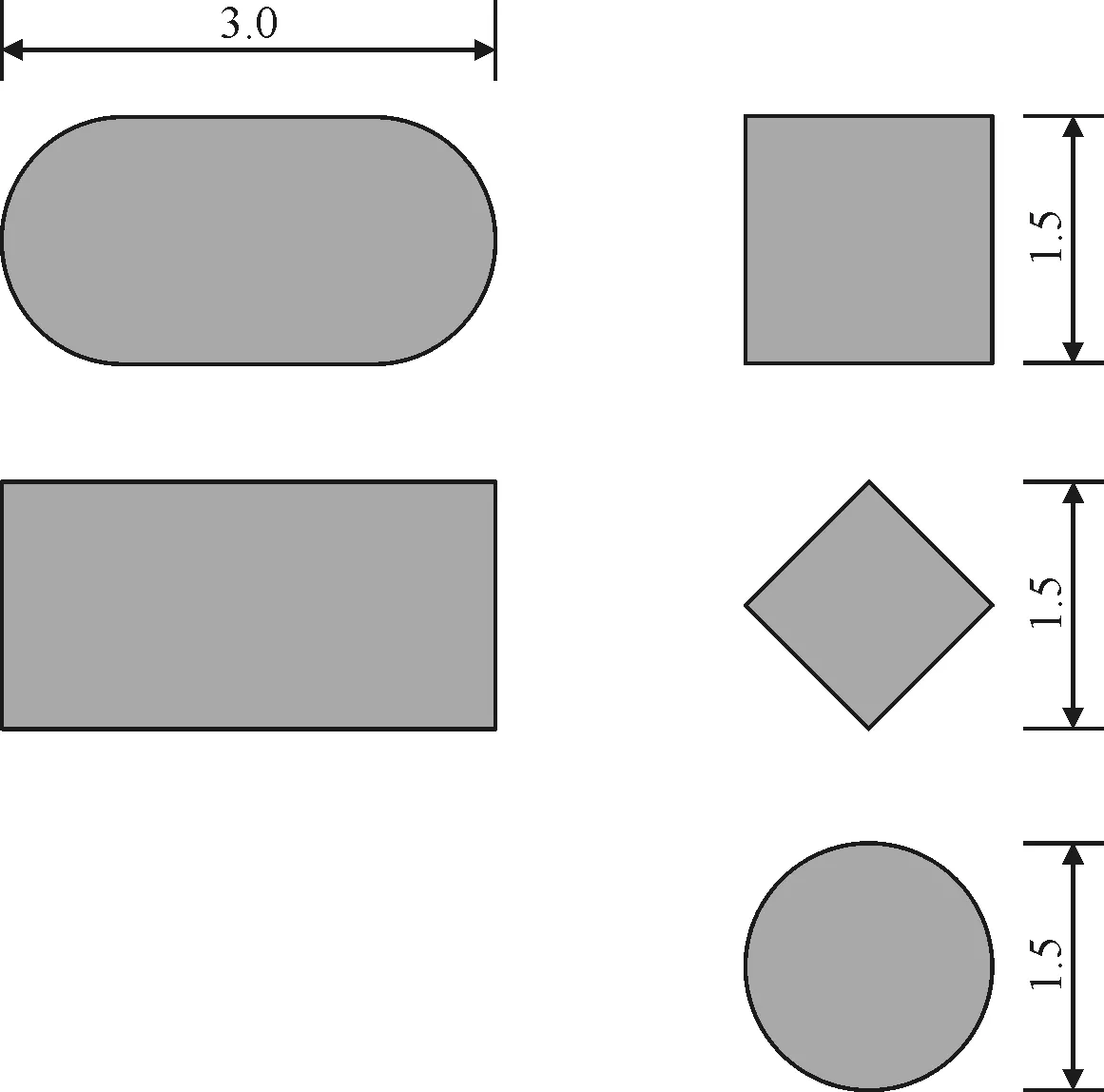
图2 柱体截面形状(单位：m)

在柱体周围建立一个14.2m×12m×10m的空间作为泥石流的流动空间，左侧和下侧用壳单元模拟，在左侧壳壁面右侧0.2m处建立SPH初始位置点，以产生SPH粒子流，如图3所示。

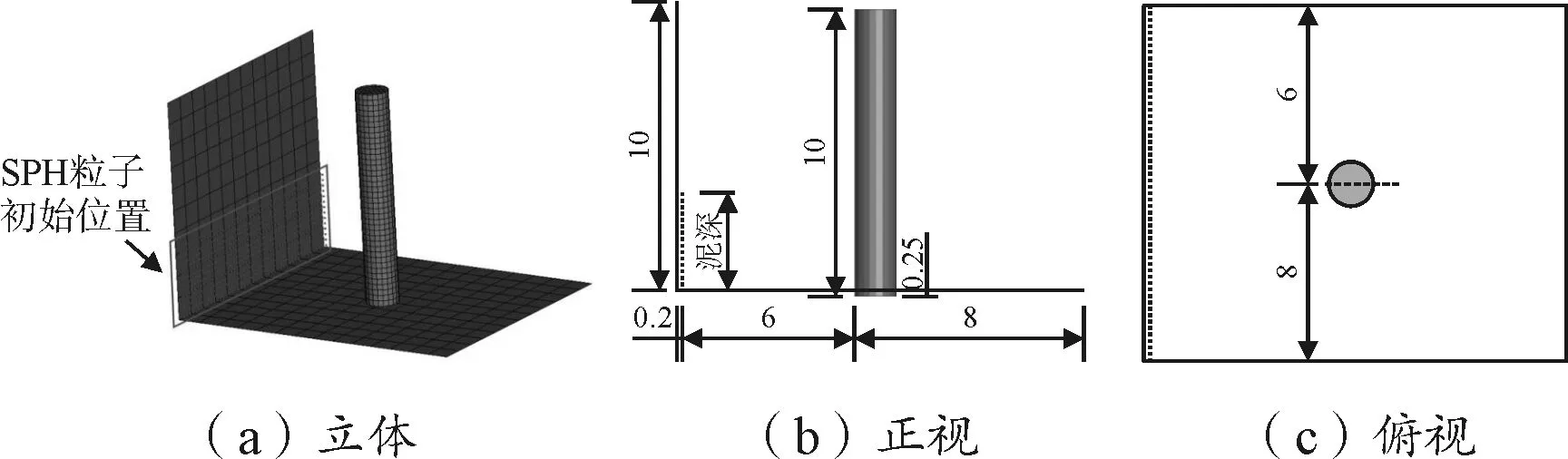
图3 几何模型(单位：m)

2.3 材料模型

因该泥石流沟细颗粒黏粒含量较少，高频率条件下泥石流以稀性泥石流为主，低频率条件下以过渡性泥石流或高容重低粘度的水石流为主，故不考虑泥石流粘度，泥石流材料模型采用*MAT_NULL模型，流变参数见表1。

泥石流的内部压强根据状态方程计算，采用Murnaghan状态方程，计算式为式(6)。

(6)

式中：ρ0为粒子的初始密度；γ为系数, 对流体常取γ=7；B为系数，计算式为式(7)。

(7)

式中：c为人工声速，c≥10vmax，vmax为流体运动过程中的最大速度。

柱体采用混凝土连续盖帽模型[14](*MAT_CSCM_CONCRETE)，该模型是美国联邦公路管理局为研究公路防撞护栏而开发，适用于低速撞击等情形。材料密度取2 400kg/m3，其余参数采用默认值及参考文献[14]，具体参数见表2。

表2 柱体材料参数

左侧和下侧壳单元边界不考虑变形，采用刚体材料模型。

2.4 边界条件

SPH粒子两侧采用LS-DYNA中SPH对称平面边界(*BOUNDARY_SPH_SYMMETRY_PLANE)，如图4所示。该方法为SPH边界处理方法中的虚粒子法，在对称平面处生成镜像粒子，以避免算法造成的SPH粒子向边界聚集问题。此外，为节约计算时间，对SPH粒子设置激活区域，运动出此区域的粒子将失活，不再参与计算，如图5所示。

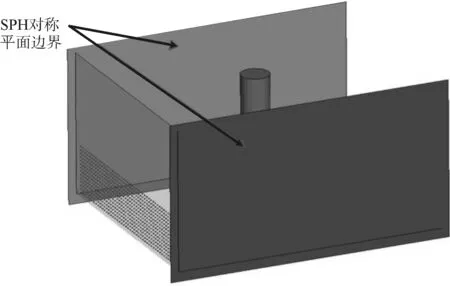
图4 SPH对称边界条件

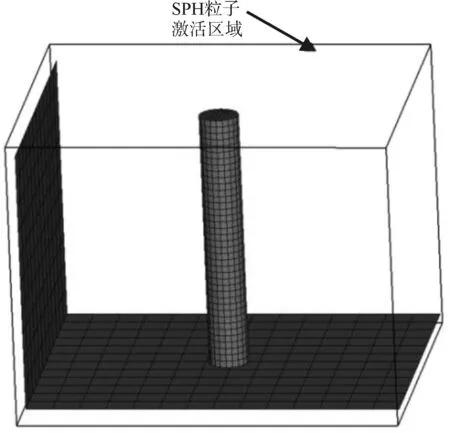
图5 SPH粒子激活区域

柱体边界条件为约束底面节点全部自由度。壳单元在材料模型里约束全部自由度。

泥石流和柱体以及下侧河道采用点面自动接触的方式。泥石流和柱体的摩擦系数取0.12[10]。采用动力松弛方式初始化柱体模型，以消除重力导致的柱体初始振荡；对柱体进行刚性类型沙漏控制，对泥石流进行粘性类型沙漏控制。

3 计算结果

3.1 冲击过程

冲击过程以发生概率P=10%的泥石流冲击圆形柱体为例，如图6所示。t=0.95s时泥石流前端到达柱体，开始对柱体产生冲击，由于泥石流前端上层泥石流在重力作用下重力势能转化为动能，所以泥石流前端速度较大；t=2.60s时泥石流冲击爬高，持续冲击柱体，在柱体的背流侧形成无流区；t=7.65s时，随着泥石流冲击的继续进行，柱体背流区会逐渐淤积，冲击已基本稳定。

图6 冲击过程

3.2 冲击力

3.2.1 不同截面形状对冲击力的影响

泥石流发生概率P为10 %时，五种截面柱体所受来流方向冲击力大小呈增大趋势，如图7所示。初始冲击时，正方形柱体和矩形柱体所受冲击力大小基本相同，圆形柱体、圆端形柱体和菱形柱体所受冲击力基本相同；随着冲击的进行，矩形柱体所受冲击力略大于正方形柱体，均大于其它三种柱体；圆形柱体、菱形柱体和圆端形柱体所受冲击力有微小的差值，所受冲击力从小到大顺序冲击过程中首先依次为圆形柱体、菱形柱体和圆端形柱体，三种截面柱体中，菱形柱体冲击力最后稳定，最终稳定时菱形柱体冲击力略大于圆端形柱体。为了消除随机噪声，对柱体冲击力采用移动平均法处理[15]，时间窗口取1s。

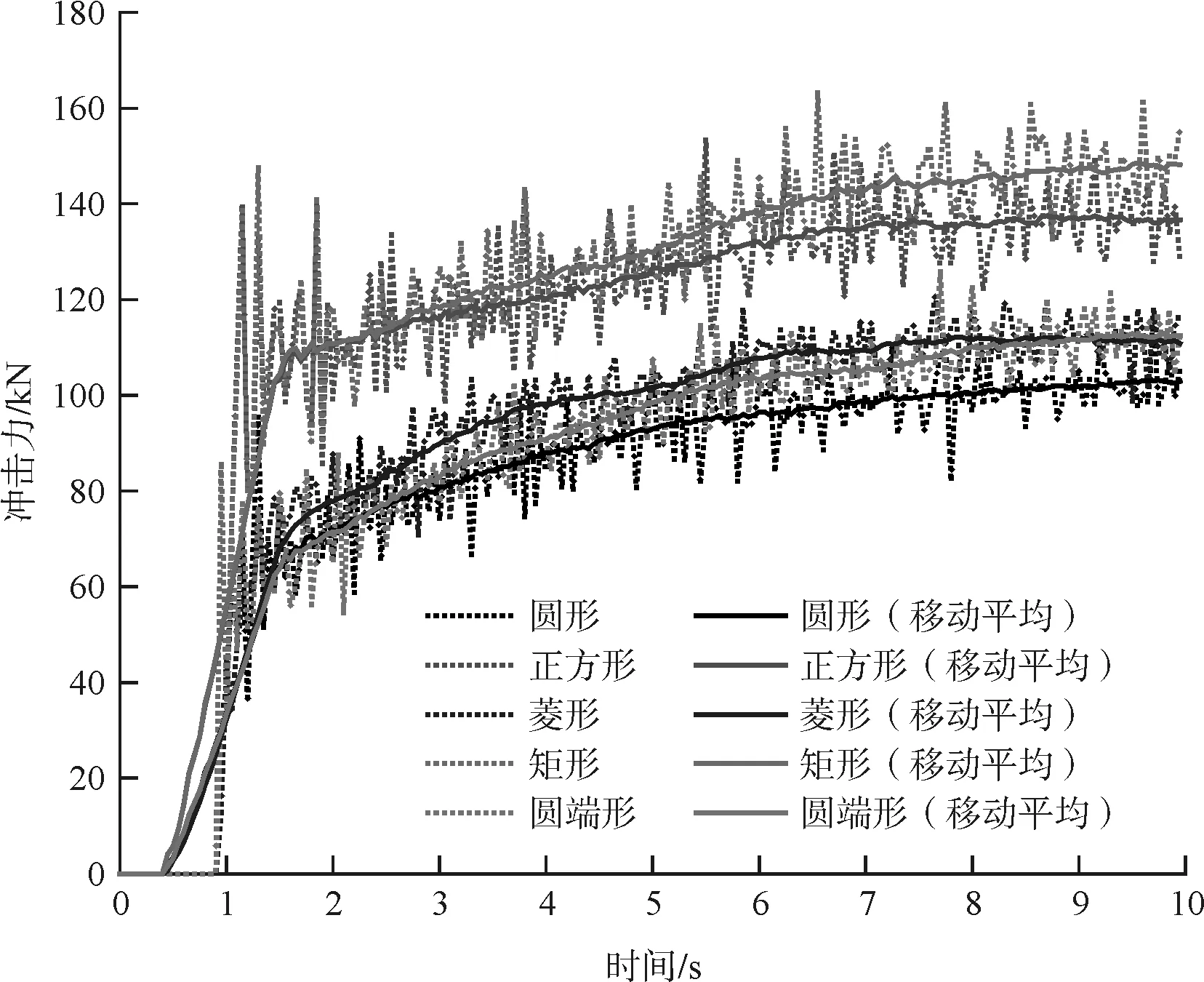
图7 泥石流发生概率P=10%条件下冲击力

对移动平均处理后的冲击力最大值进行分析，见表3。从圆端形柱体所受冲击力大于圆形柱体，矩形柱体所受冲击力大于正方形柱体可以得出：相同迎流面下，长宽比对柱体所受冲击力有一定的影响，截面长宽比越大，柱体所受冲击力越大。这是因为随着长宽比的增大，柱体侧面受到的泥石流摩擦力增大，并且与背流侧无流区淤积等多种因素有关。从正方形柱体和矩形柱体所受冲击力大于圆形柱体、圆端形柱体和菱形柱体可以得出：圆形迎流面和菱形迎流面有助于减小冲击力。这与规范给出的圆形柱体所受泥石流冲击力系数较小相一致。

以圆形柱体为基准，泥石流发生概率P=10%条件下，各截面柱体所受来流方向冲击力的移动平均最大值与圆形柱体的对比见表3。由计算可知，矩形柱体所受冲击力相较圆形柱体增加最大，为44.0 %，菱形柱体增加最小，为8.8 %。本文分析所用菱形柱体和圆端形柱体的泥石流冲击力移动平均最大值始终相近，但圆端形柱体所受冲击力受截面长宽比的影响，调整圆端形柱体横截面的长宽比可使圆端形柱体所受冲击力发生变化。

表3 冲击力最大值(移动平均)对比

3.2.2 不同发生概率泥石流对冲击力的影响

分析各截面柱体在不同发生概率泥石流条件下的冲击力，并采用移动平均法计算得到其最大冲击力，如图8所示。总体来看，不同发生概率泥石流冲击力，均是矩形、正方形截面柱最大，其余三种截面最大冲击力接近。以泥石流发生概率P=10%为基准，各截面柱体所受来流方向冲击力的移动平均最大值与P=10%条件下的对比见表4。由表4可知，P=5%条件下，各截面柱体所受冲击力增加40 %～50 %左右；P=2 %条件下，各截面柱体所受冲击力增加100 %～110 %左右；P=1%条件下，各截面柱体所受冲击力增加190 %～210 %左右。

图8 不同概率条件下最大冲击力大小对比

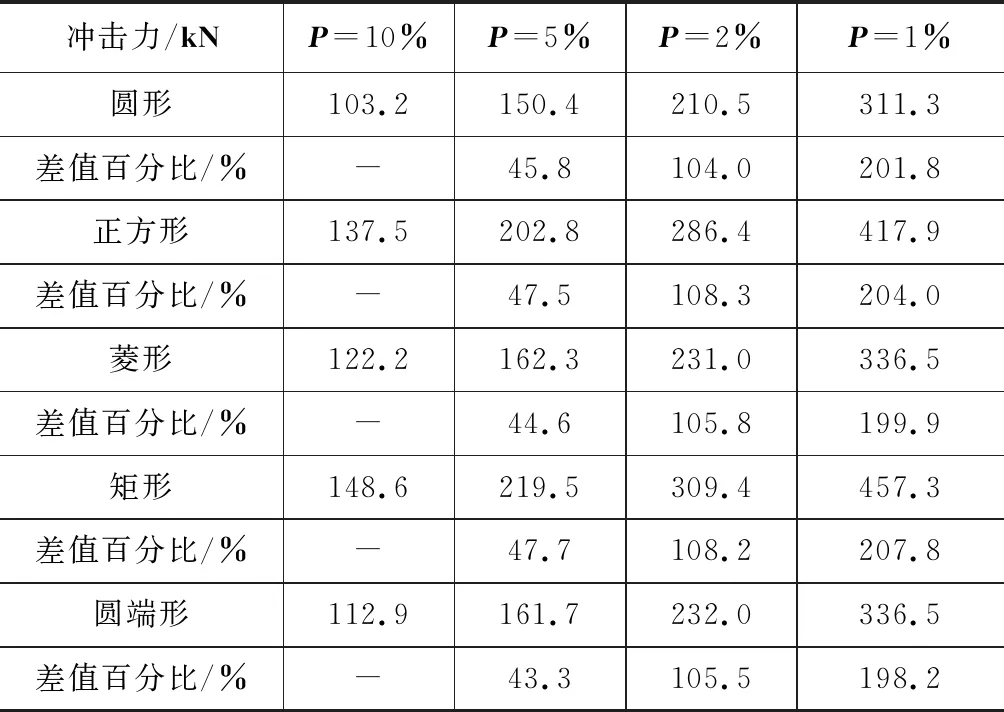
表4 不同概率条件下最大冲击力比较

3.3 柱顶水平位移

泥石流发生概率P=10%条件下菱形柱体水平位移最大，其次依次为正方形柱体、圆形柱体、圆端形柱体和矩形柱体，见图9。柱顶水平位移与其截面的惯性矩及所受水平力的大小和分布有关。本文所选择的5种截面形式，圆形、正方形、菱形、矩形、圆端形的截面惯性矩比值为1.0∶1.69∶0.42∶3.38∶2.70。菱形的截面惯性矩最小，且其所受水平力比圆形还大，因此其柱顶的水平位移最大。随着泥石流发生概率的减小，由于泥石流的容重、速度均增大，因此各截面柱的冲击力增大，导致柱顶水平位移增大，如表5所示。

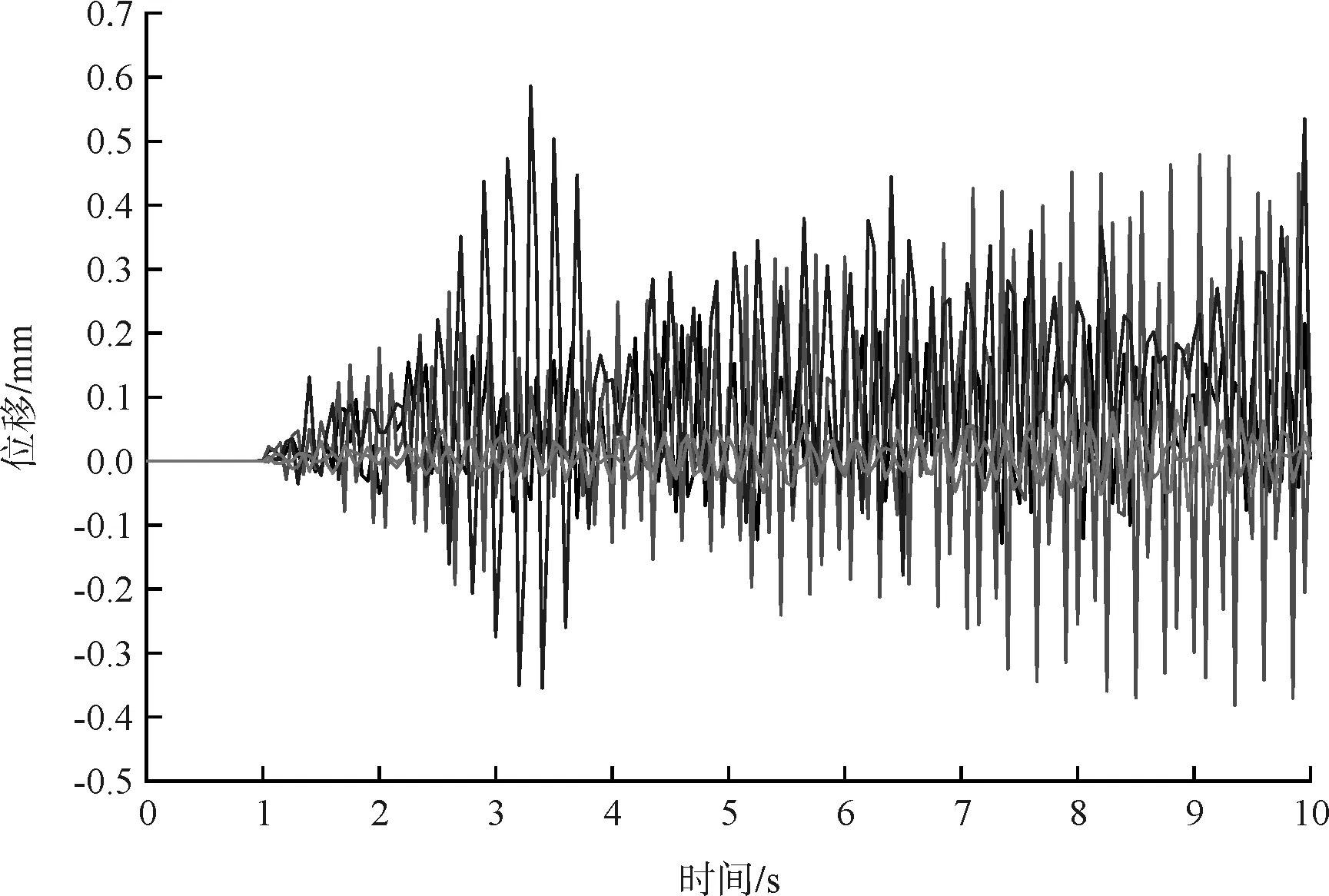
图9 P=10%条件下柱顶关键点位移时程

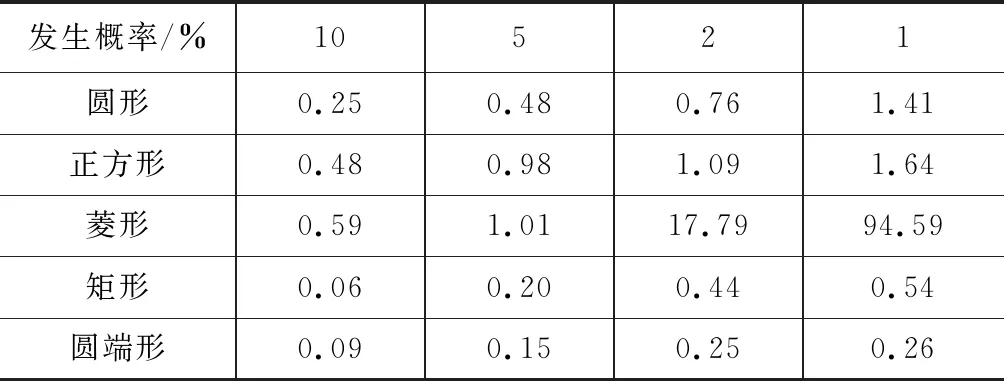
表5 柱顶最大水平位移mm

但是当P=2%、P=1%时，菱形截面柱体的位移急剧增大，且在新的位置来回振动，如图10所示。主要是由于菱形截面柱的刚度最小，在较大泥石流的冲击下，菱形截面柱体混凝土出现了大面积的损伤，柱体受力性能变差，使得柱体不能维持原来的平衡。

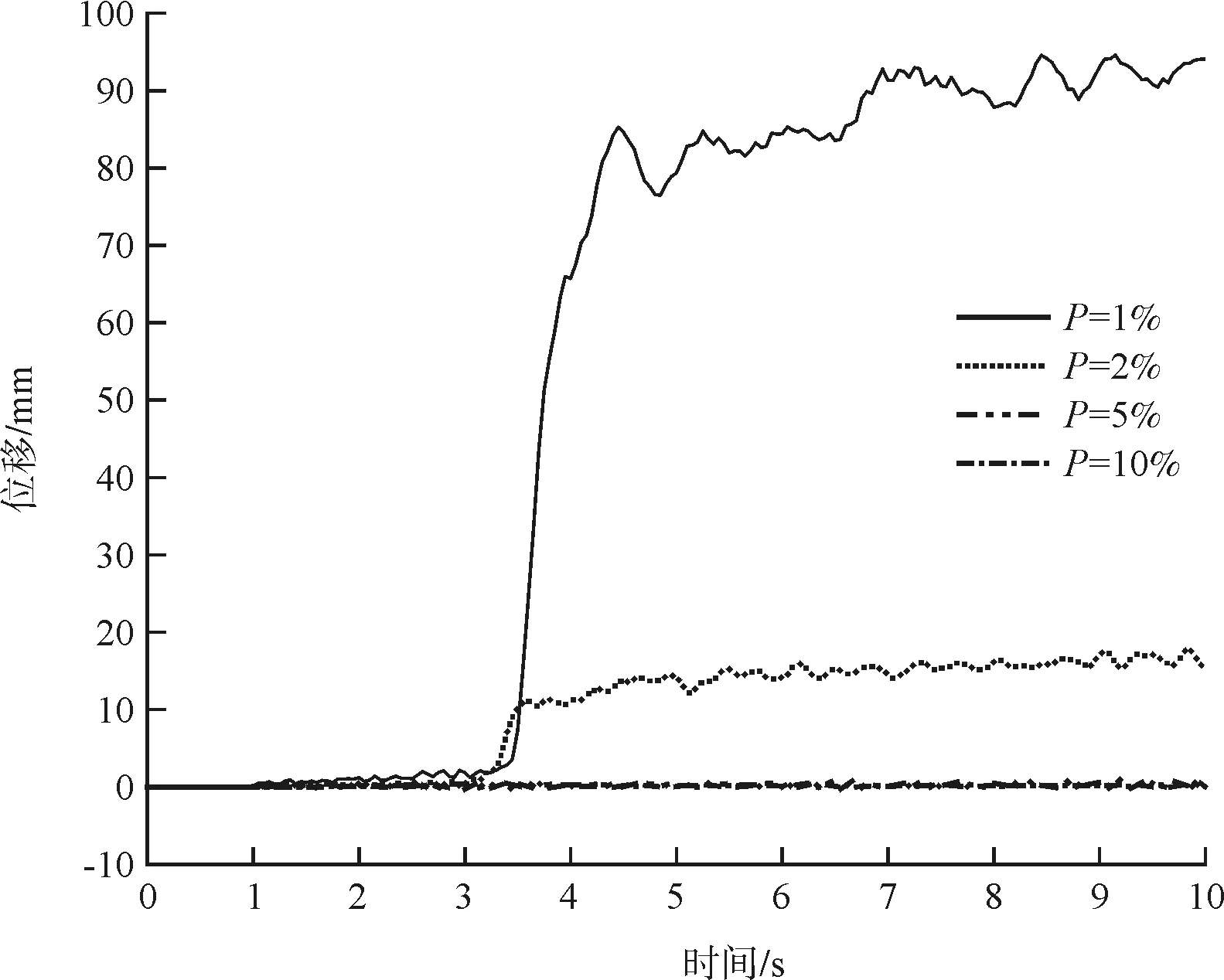
图10 菱形柱体柱顶关键点水平位移时程

4 结论

SPH-FEM耦合的方法能够很好地模拟泥石流冲击柱体时迎流侧冲击爬高、背流侧无流区域以及背流区泥石流淤积等冲击过程。

(1)相同发生概率泥石流冲击下，冲击稳定后矩形柱体所受冲击力最大；柱体横截面长宽比对冲击力有一定的影响，长宽比越大，所受冲击力也越大。

(2)不同发生概率泥石流条件下，由于泥石流的容重、速度均增加，导致冲击力均有不同程度的增加。

(3)同等条件下，菱形截面柱由于其刚度最小，导致其柱顶水平位移大于其它几种截面柱，其受力性能最差，也最容易发生损毁，在结构设计中应避免选择这种截面形式。

在本文的研究中仍存在一些局限：在采用SPH方法模拟泥石流浆体时，未考虑泥石流浆体的粘性；对泥石流建模时只考虑了泥石流浆体，未考虑泥石流中的粗颗粒和大块石；对柱体底面的约束过于理想化等。这些需要继续研究。