关于挡土墙边坡支护设计建模的探讨

林之航

（福州市规划设计研究院集团有限公司，福建 福州 350100）

目前，我国正处于基础建设高速发展期，边坡工程设计是工程技术人员必须掌握的技能。一般来说基础设施建设项目对工期要求都比较严格，这就对设计人员的工作效率就提出了较高的要求，在保证具有足够安全的条件下，如何快速地进行边坡支护设计是所有工程师都较为关心的问题。而建模计算是初步设计的首要步骤，合理的模型尺寸将大大的缩减边坡整体稳定性计算的速度。因此，本文对建模过程中影响稳定性计算的因素进行了研究。

1 影响稳定性计算的因素

为了研究建模计算中对稳定性安全系数的影响因素，采用理正岩土6.5PB2软件对挡土墙支护的边坡整体稳定性进行了一系列的类比计算，基础土层计算参数详见表1。

1.1 土柱误差取值的影响

影响稳定性安全系数的计算结果其实有很多。本文利用一工程实例的常规建模计算，发现挡土墙支护边坡在整体稳定性计算中存在的问题。计算模型详见图1（图中A是指建模时墙后所取的水平距离，B是指坡脚前所取的水平距离，C是指坡脚以下所取的竖直深度，3个字母全文所表达的意思均相同），计算结果详见表2。该计算参照了设计人员的常规操作。首先为了提高计算速度，选择一定的土柱误差来计算，此次计算土柱误差取0.5 m。为了便于比较分析，图1中的B值取10 m、C值取15 m且为定值。同时，由于墙前土在设计中的作用经常被作为安全储备来考虑，故这里对墙前土层对稳定性安全系数的影响暂不做考虑。从计算结果中发现填土面若为水平，随着A值得变化，起初边坡整体稳定性安全系数并没有变化，而且滑动面和圆心也没有任何变化，当A值为19.5 m和20 m时，稳定性安全系数明显变小，而后当A值达到20.5 m后又恢复到了之前的计算值且滑动面和圆心也恢复到了之前的位置。

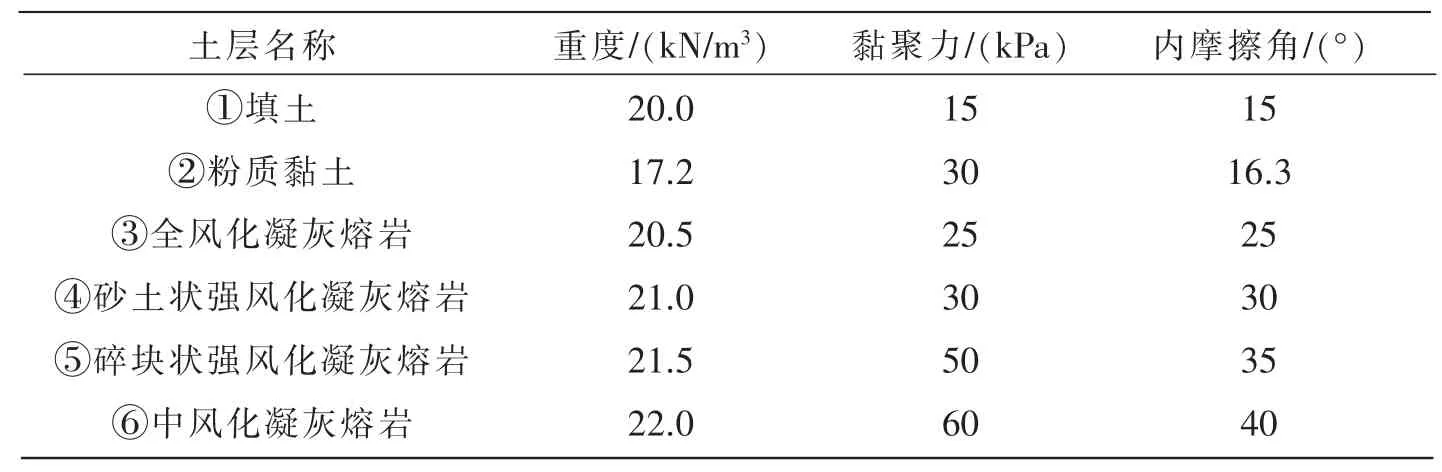
表1 基础计算参数表

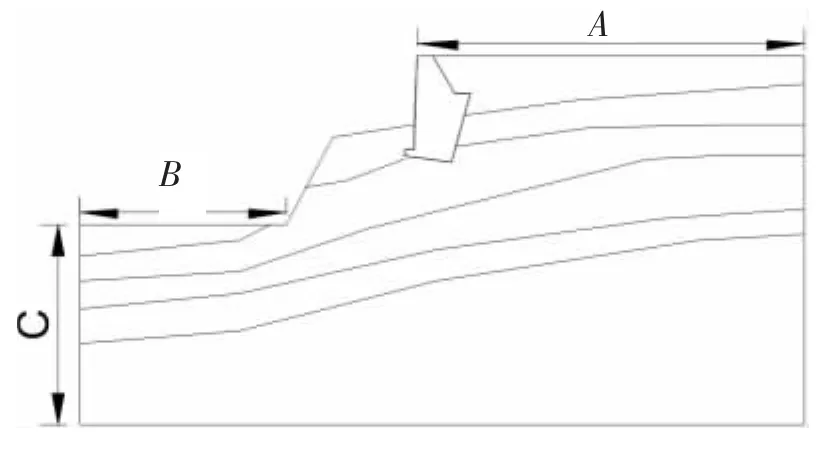
图1 挡土墙支护边坡稳定性计算示意图

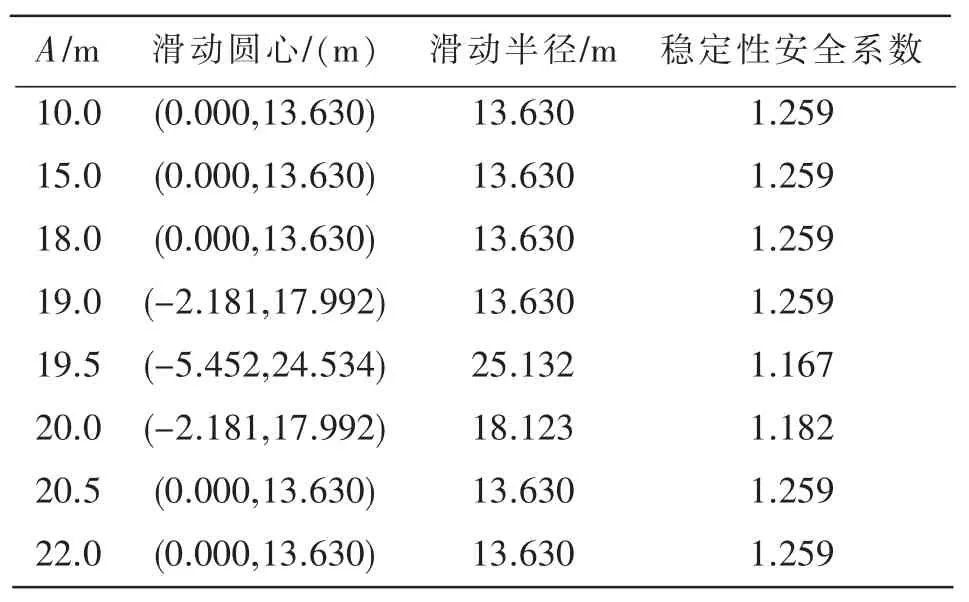
表2 边坡稳定性计算表（土柱误差取0.5）

产生该变化的主要原因是计算中取了土柱误差为0.5 m。当取土柱误差为0进行计算时，发现实际上A值取19.5和20时，若土柱误差取0，计算所得的结果和A值取其他数值时是相同。该计算结果说明在建模时，由于忽略土柱误差计算所得的稳定性安全系数差值可达到0.09，这将会对边坡整体稳定性的判定产生影响，设计人员不能为了节省计算时间，计算中直接忽略土柱误差所带来的影响。

规范中要求支护后一般工况下坡体稳定性安全系数要超过1.35，若所仅作稳定性判定，计算所得的稳定性安全系数超过1.35较多时，忽略土柱误差对计算结果不会产生较大的影响，但如若计算结果接近1.35时，应该要进行精确的计算。

1.2 填土面倾角变化的影响

1）稳定性安全系数的变化规律

挡墙后填土面往往并不是水平的，为了研究填土面坡角的变化对稳定性安全系数的影响，本文对填土面与水平面夹角为7°、10°、15°、20°时，不同的A值情况下边坡稳定性安全系数进行了计算，计算模型见图2，计算结果可以参见图3。从图3中可以发现，当填土坡角为7°、10°、15°时，边坡稳定性安全系数随着A值得改变，变化并不大，变化量基本都在0.01左右，这对一般的计算结果并没有太大的影响，一般不会对边坡整体稳定性的判定产生影响。

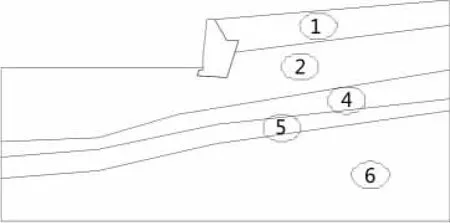
图2 填土面倾角为7°时的计算模型

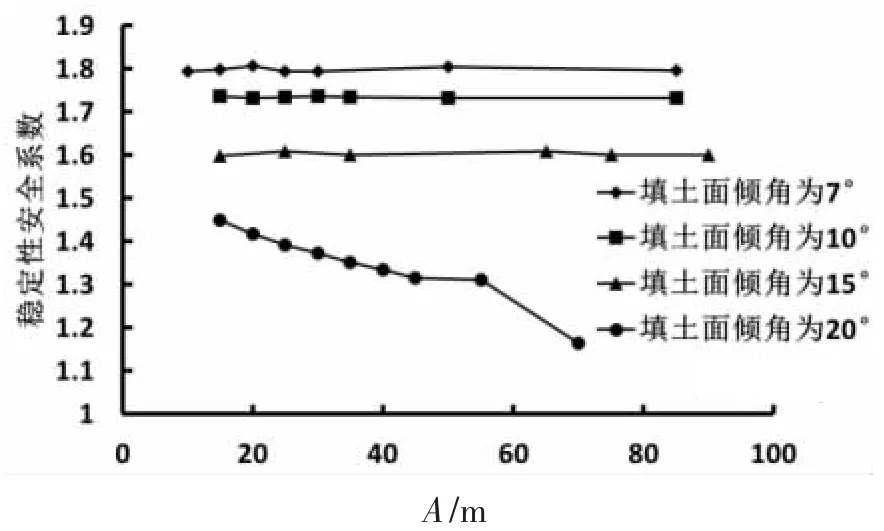
图3 A值与边坡稳定性安全系数关系曲线

但是，当坡角达到20°时，随着A值的不断增大，计算所得的稳定性安全系数不断的变小。而且下降速度在A值超过55后明显加快。这说明当填土面坡角较大时，建模时对A值就需要有所考虑。为此针对坡角为20°情况，本文进行了进一步的分析计算，发现若填土坡面后存在一个水平平台时，计算所得的稳定性安全系数就不再有大的变化。从定性的角度来看，建模时若填土面倾角较大时，要将这个土坡包含进来。

从上述的结果发现填土土坡坡脚大于15°后才对边坡稳定性安全系数的计算产生较大的影响，由于计算中填土参数取值为内摩擦角15°，黏聚力为15 kPa。刚好和填土的内摩擦角相等。为了研究填料内摩擦角是否存在边坡稳定性计算影响因素的阈值，同时对黏聚力为15 kPa，内摩擦角为20°的填土材料在不同坡角和不同A值情况下的稳定性安全系数进行了计算。计算结果如图4所示。

从图4中可以发现，当填土坡角为7°和15°时，边坡整体稳定性安全系数仍旧没有随着A值的改变而产生较大的变化。当填土面倾角达到20°时，边坡整体稳定性安全系数，随着A值的增大而不断的减小，这和内摩擦角取15°时的计算结果所显示出来的规律相同。

同时，从计算结果中可以发现，内摩擦角取值从15°变为20°时，边坡的稳定性安全系数几乎是没有变化的。而黏聚力、重度的变化对稳定性安全系数的影响和内摩擦角的基本相似，如图5和图6。当黏聚力取10 kPa，填土坡角为7°和15°时，边坡整体稳定性安全系数仍旧没有随着A值的改变而产生较大的变化。当填土面倾角达到20°时，边坡整体稳定性安全系数，随着A值的增大而不断的减小。同样的规律也出现在重度取16 kN/m3的类比计算结果上。

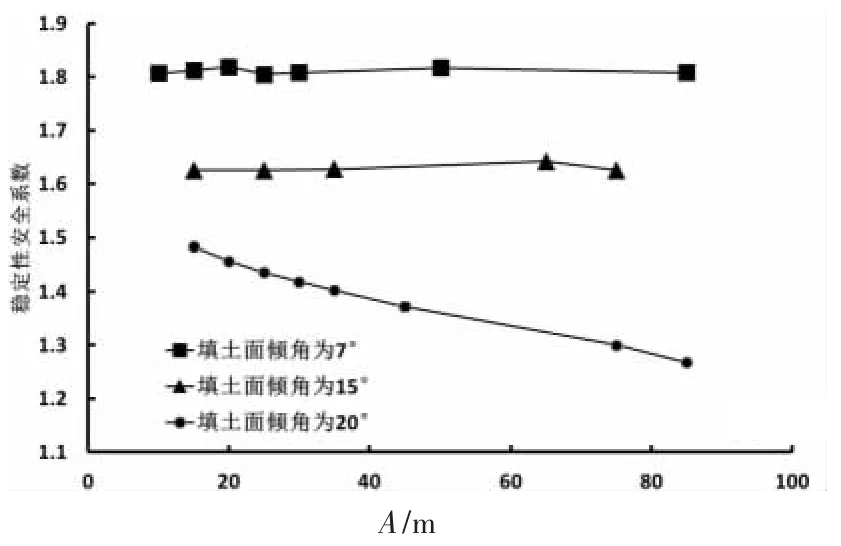
图4 A值与边坡稳定性安全系数关系曲线(填土内摩擦角为20°时)

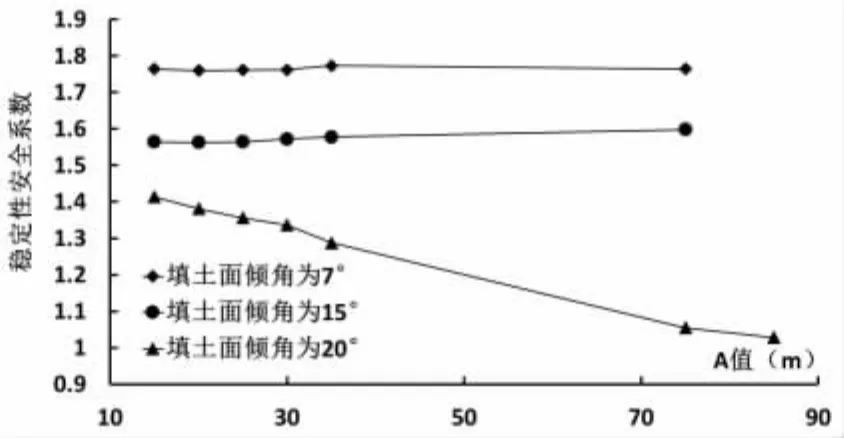
图5 A值与边坡稳定性安全系数关系曲线(填土黏聚力为10kPa时)

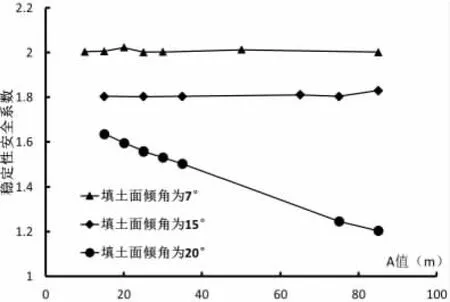
图6 A值与边坡稳定性安全系数关系曲线(填土重度为16kN/m3时)

从以上的计算结果可以发现，对稳定性安全系数变化规律产生影响的主要因素是填土面倾角的大小。为此，本文进一步对坡角为 16°、17°、18°、19°的边坡整体稳定性进行了计算。计算结果如图7所示。

从图7中可以看出坡角为16°时，A值的变化并对稳定性安全系数没有太大的影响，而坡角为18°和19°时，A值的变化对稳定性安全系数的影响较大，基本上随着A值得增大而不断的变小。当坡角为17°时，先是随着A值的增大，稳定性安全系数基本没有变化，当A值增大到45m时，稳定性安全系数开始随着A值得增大而减小。

2）滑动面变化规律

上述分析主要针对稳定性安全系数的变化，本小节主要是利用上述的计算成果来分析滑动面的变化规律。限于篇幅，仅列出图3中计算结果所对应的滑动面。如图8所示。

为保持图形清晰，便于表达。图8中列出的是坡角为 7°、10°、15°时，A 值取 15 及 85计算得出的边坡滑动圆弧的位置。以及坡角为20°时，A值取15及25计算得出的边坡最危险滑动圆弧的位置。从图中可以看出当填土面倾角为 7°、10°、15°时，A 的取值虽然相差70，但滑动面的位置基本没有太大的变化，相应的稳定性安全系数也基本没有变化。而当坡角为20°时，A值虽然只相差10，但其最危险滑动面的位置却发生了较大的改变，其相应的稳定性安全系数也有较大的变化。

从计算中还发现当所取的A值对稳定性安全系数有较为明显的影响时，其计算所得的最危险滑动面往往会超出所建立的模型区域，如图9所示。图是填土面倾角为17°时的滑动圆弧，图中数字所代表的是A值的大小，滑动面依次是A值取15、20、25、30、35、40时计算所得的最危险滑动面。在填土面倾角为18°和19°时，计算所得最危险滑动面也呈现出相同的规律。

图7 A值与边坡稳定性安全系数关系曲线（填土面倾角为 16°～19°时）

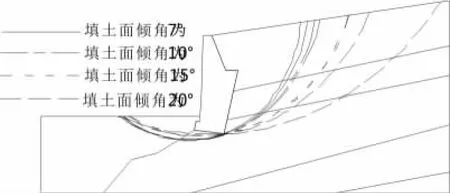
图8 滑动圆弧随A值变化示意图

2 结论

1）采用理正建模计算土体稳定性时，若忽略土柱误差，当稳定性安全系数接近1.35时，可能会对边坡稳定性的判定产生影响。

2）若墙后填土面不是水平的，当倾角达到17度时，所建的模型中，墙后的水平距离的大小将对稳定性安全系数有较大的影响。随着A值的增大，稳定性安全系数不断地减小。

3）当倾角超过一定的角度后（在计算实例中为17°），若随着A值的增大，稳定性安全系数不断地减小，此时计算所得的最危险滑动面往往会超出所建立的模型区域。

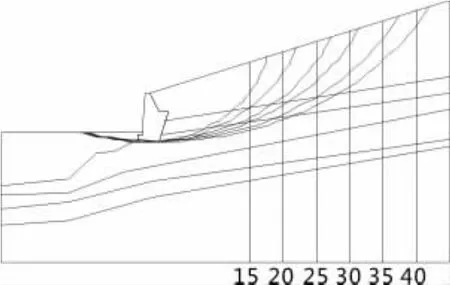
图9 滑动圆弧超出建模区域示意图