例谈线段2倍关系的证明策略

苏明海 苟述珍

[摘要]平面几何作为初中课程内容四大板块之一，一直是中考考查的重点，分析线段关系是解决平面几何问题的必备能力.文章通过对一道例题的分析与求解，谈谈线段2倍关系的证明策略

[关键词]2倍;线段关系;证明策略

作者简介：苏明海（1968-），本科学历，中学高级教师，重庆市骨千教师，重庆教育学会教育管理常务理事，从教31年，一直从事初中数学教学工作和教学管理工作，论文《初中数学目标教学有效途径和方法》获全国目标教学论文评比一等奖;苟述珍（1992-），硕士研究生，中学二级教师从事中学数学教学工作

《义务教育数学课程标准（2011年版）》将初中课程内容分为四个板块，图形与几何”作为其中之一，足见其分量.平面几何在发展学生的逻辑思维，培养学生的推理能力方面有着非常重要的作用，是初中数学教学的重点内容之一，也是全国各省市中考必考内容线段2倍关系是平面几何的考查热点，但学生在问题解决上的表现差强人意则源于题目本身难度，另则源于学生方法和思维的局限性.笔者希望以本文总结线段2倍关系的证明策略，拓宽解题思路，增强学生灵活应变的能力.

例题呈现

（2019重庆模拟）已知平行四边形ABCD中，DE⊥BC于E，点F是DE上点，满足BA⊥BF，连接CF

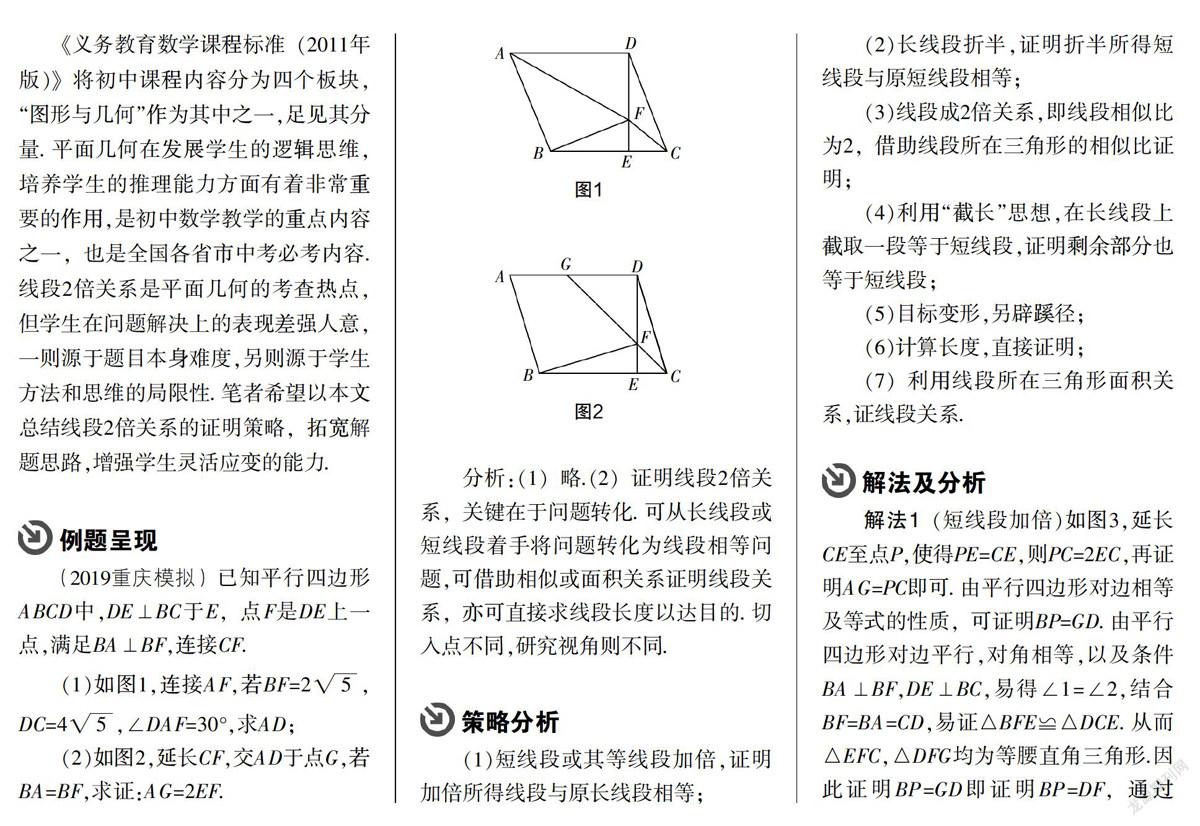
（1）如图1，连接AF，若BF=2V5DC=4V5，∠DAF=30°，求AD

（2）如图2，延长CF，交AD于点G，若BA=BF，求证：AC=2EF

分析：（1）略.（2）证明线段2倍关系，关键在于问题转化.可从长线段或短线段着手将问题转化为线段相等问题，可借助相似或面积关系证明线段关系，亦可直接求线段长度以达目的.切入点不同，研究视角则不同.

策略分析

（1）短线段或其等线段加倍，证明加倍所得线段与原长线段相等

（2）长线段折半，证明折半所得短线段与原短线段相等;

（3）线段成2倍关系，即线段相似比为2，借助线段所在三角形的相似比证明

（4）利用“截长”思想，在长线段上截取一段等于短线段，证明剩余部分也等于短线段

（5）日标变形，另辟蹊径6）计算长度，直接证明;

（7）利用线段所在三角形面积关系，证线段关系.

解法及分析

解法1（短线段加倍）如图3，延长CE至点P，使得PE=CE，则PC=2EC，再证明AC=PC即可.由平行四边形对边相等及等式的性质，可证明BP=CD.由平行四边形对边平行，对角相等，以及条件BA⊥BF，DE⊥BC，易得∠1=∠2，结合BF=BA=CD，易证△BFE≌△DCE.从而△EFC，△DFG均为等腰直角三角形.因此证明BP=CD即证明BP=DF，通过△BPF≌△DFC可解.

解法1通过将短线段加倍，然后证明加倍后所得线段PC与原长线段AG相等，结合图3中阴影部分的旋转全等结构，以及平行四边形的性质为问题转化提供途径.线段2倍关系是a+b=c，即两条短线段之和等于长线段的特殊形式

短线段加倍的实质是“补短”，AB=BF，BA⊥BF，隐含了等腰直角的背景和旋转全等的结构，因为EF=EC，构造2EC即构造2EF，因此有如下解法2.

解法2（短线段的等线段加倍）如

图4，延长EF到点の，使得EF=EQ，则FQ=2EF=2EC，因此证明AG=FQ即可.而证明AG=FQ，可通过A4G，PQ分别所在三角形全等得证，即如图5，△ABG≌△FBQ;也可借助DG=DF，将问题转化为证明DA=DQ，此问题可通过证明△DAQ为等腰三角形来解决，如图6;或通过证明△BAD≌△BQD来解决，如图7，详细过程不再赘述

解法2和解法1的实质为同一方法均以加倍的方式将证明线段2倍关系问题转化为证明线段相等的问题，结合图形背景，便有通过图形全等证线段相等，即图5;通过等腰三角形及等式的基本性质证线段相等，即图6;通过全等及等式的基本性质证线段相等，即图7.解法1将短线段自身直接加倍，解法2则是将短线段的等线段加倍，均为直接加倍.在解题过程中，结合题目背景还可间接加倍，如利用中位线的性质，短线段作为中位线，其所对第三边即为其2倍.直角三角形斜边中线定理，含30°的直角三角形边之间关系定理，也是2倍线段的生长根基.

解法3（长线段折半）如图8，连接BD，BG，由解法1知，BE⊥DE，BE=DE则∠BDE=45°，而△GDF为等腰直角三角形，易得BD为GF的垂直平分线，因此BC=BF，而BF=BA，故△ABG为等腰三角形，长线段AC作为等腰三角形的底边，对其折半，自然联想“三线合一”，过点B作BH⊥AG，则H為AG中点，AH=HG=AC，借助△ABH≌△CDE，从而得证.

解法3将长线段折半，证明一半与短线段相等的方式也是证明线段2倍关系的常用方法.若长线段是等腰三角形的底边，作“三线合一”是常用思路，当然，亦可直接取长线段的中点.

解法4（相似）如图9，连接AF，根据平行四边形对角相等，可得∠BAD=∠DCB，而△ABF，△EFC，△GDF为等腰直角三角形，因此∠BAF=∠ECF=∠EFC=∠DCF=45°，故∠GAF=∠FCD，∠AGF=∠CFD，因此△AGF～△CFD，所AGGAV2，则AG=V2CF=CFFD2EC，从而得证.

线段的倍数关系即为线段的比例关系，由比例联想相似，这是借助相似解决倍数关系的出发点

解法5（等式的基本性质）如图10在AC上截取AM=EC，连接BM.根据平行四边形的性质，知AB=CD，∠A=∠DCE，因此截取AM=EC，即有△AMB≌△CED再证明MC=EC即可.由解法1知DE⊥BE且DE=BE，易得四边形MBED为正方形，根据MD=ED，GD=FD，结合等式的性质，显然MG=EFE因此AG=AM+MG=EC+EF=2EC，得证.

正如前文所说，线段2倍关系是a+b=c即两条短线段之和等于长线段的特殊形式，因此可用解决a+b=c的方法来解决此问题，解法1的实质是“补短”，解法5的实质则为“截长”，在长线段AG上先截取一段等于短线段EC，再证明剩余部分MG也等于短线段EC，是一般方法在特殊背景下的应用

解法6（日标变形）证明AG=2EC即证明A4C=V2EC.如图1，过点B作V2BN⊥BC交FG的延长线于点N，连接AN，则△NBC为等腰直角三角形，结合BA⊥BF且BA=BF，得“手拉手”型全等，即△ANB≌△FCB，则AN=FC，同时进而可推出∠NAG=∠NCGA=45°，△ANG为等腰直角三角形，因此M=CFC=V2EC，则AG=2EC，得证.

任何线段关系的证明问题，都可以将目标式子进行等价变形，证明变形后的式子即可.变形方式应结合题目背景及条件而定，比如解法6依据图中暗含的多处45°，易构或证明V2倍，因此做如上变形，变形后的式子可给学生新的解题构图方向，从而另辟蹊径，解决问题

解法7（计算长度）如图12，由解法1知△EFC，△DFG均为等腰直角三角形，不妨设EC=EF=a，DC=DF=b，则DE=BE=n+b，因此BC=BE+EC=a+b+a=2a+b根据平行四边形对边相等，故AD=BC=2a+b，所以AG=AD-DG=（2a+b）-b=2o=2EC，得证.

解法7借助条件中线段之间的关系，直接求出线段AG，EC的长度，从而证明线段2倍关系.不仅是线段2倍关系的问题，任何线段和差倍分问题，只要能将线段长度求出，或者用同一字母进行表示，均可得以解决

解法8（利用面积）如图13，连接BD，则S。8m=SBE，由解法3知BD为CF的垂直平分线，因此Smc=Smr，故SABeSBE+S2me，即S=S2+S3，由解法1的分析知S，=S，所以S，=2S3，而△ABG与△CDE等高，面积之比等于底之比，从而得到AG-2EC通常，依据等高的两个三角形面积之比等于底之比，或者等底的两个角形面积之比等于高之比，将线段的倍数问题转化为面积的倍数问题，从而启发学生新的解题思路，解法8即是如此.

结语

线段2倍关系问题是平面几何的考査热点，学生经常因为方法的局限性，致使解題受阻，因此建立方法体系很有必要.除上述方法之外，在直角三角形中可通过证明锐角为30°，从而证明斜边为短直角边的2倍，也可通过证明三角形为直角三角形，从而证明斜边是斜边上的中线的2倍.笔者希望学生通过数学知识和数学方法的学习，数学思想的领悟以及态度、情感的熏陶逐渐形成正确的价值观念、必备品格和关键能力.折半、加倍以及一般形式的“截长补短”是解决此类问题的通法，教学中教师应用好课堂这个主渠道，特别加以引导，结合教学内容落实四基，培养四能，促进学生数学学科核心素养的形成和发展.