考虑分布参数不确定的换热器封头结构优化研究*

彭 翔，徐小青，李吉泉，姜少飞

(1.浙江工业大学 机械工程学院，浙江 杭州 310014； 2.浙江大学 流体动力与机电系统国家重点实验室，浙江 杭州 310027)

0 引 言

板翅式换热器由封头、导流片、翅片、隔板等结构组成，具有体积小、重量轻、传热效率高、可同时处理多种冷热流体等优点，广泛应用于空气分离、航空航天和交通运输等行业。其中，换热器封头主要作用是将进入换热器的冷热流体均匀分散到多层翅片组成的流道区域，封头流量分配均匀性是影响翅片区域换热效率的关键因素[1-3]。

国内外学者开展了一系列封头结构优化设计方面的研究工作，通过改变封头内部流体流动状态，进而改善封头出口的流动均匀性。王伟等人[4]研究了封头结构对换热性能的影响，结果表明封头结构对换热器内流量分配和温度分布均匀有很大影响；YANG H等人[5]定量评价了多通道换热器中流动不均匀性的影响，通过对比常规封头、打孔挡板封头和Quasi-S型封头的性能，发现了Quasi-S型封头的流动均匀性最好，能有效提升换热性能；CHIN W M[6]基于代理模型和流体动力学分析，以出口处液相绝对质量流率差最小为优化目标，确定了分配效果最佳的封头结构参数值。

目前，封头结构优化设计的相关研究都假定所有设计变量为确定性变量。但在实际工程应用中，由于制造误差、工况波动等因素影响，封头结构与工况变量均为不确定性变量。且对于小批量制造的大型板翅式换热器封头结构，由于制造样本少、测量误差等影响，设计变量的分布参数和分布类型往往也是不确定的。结构和工况变量不确定性对封头内部流动不均匀性和压降均有严重的影响[7]，进而影响换热器的总换热效率。

针对该问题，本文提出一种考虑分布参数不确定的换热器封头结构优化设计方法。笔者首先进行封头结构变量不确定来源分析，确定分布参数不确定性的表达函数；然后基于预测区间准则和遗传算法，构建封头结构变量与封头流动不均匀度的自适应Kriging近似模型；最后建立换热器封头结构优化设计函数，实现以流动不均匀度最低为优化目标的封头结构变量不确定性优化设计，获取最佳封头结构尺寸值，实现考虑分布参数不确定的换热器封头结构优化设计。

1 问题描述

常见的换热器封头类型包括：瓜皮式封头、打孔挡板封头以及S弯改进型封头[8，9]等。瓜皮式封头由输送流体的总管和分配流体的壳体组成。为了改进换热器的换热效果，很多学者在传统瓜皮式封头内部加上打孔挡板，以提高封头内部流体分配的均匀性。

笔者使用的打孔挡板封头二维模型如图1所示。

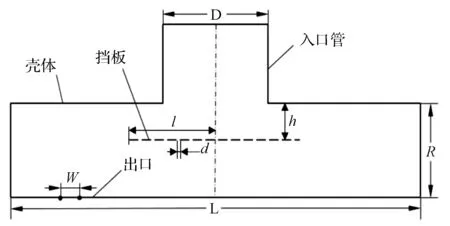
图1 使用的打孔挡板封头二维模型

图1中，封头长度L、入口管直径D、封头瓜皮结构半径R、出口尺寸W与文献[10]一致，分别为L=452 mm、R=77 mm、D=100 mm、W=12 mm。分析挡板孔径d、挡板安装高度h和挡板长度l3个结构参数不确定性对封头性能的影响。

为了保证挡板孔在挡板上均匀分布、且中心线出有挡板孔，当封头出口数n为奇数时，挡板孔数量设置为2n+1；当封头出口数n为偶数时，挡板孔数量设置为2n；挡板孔间距根据挡板孔数量、挡板孔径、挡板长度，以挡板孔在挡板上均匀分布为原则，进行自动分布确定。

由于制造误差、安装误差等因素影响，挡板结构尺寸实际值与设计值间存在误差。

为了充分考虑各种不确定性来源，笔者把设计变量及其分布参数的不确定性统一量化表征为正态分布，根据3σ法则确定挡板孔径d、挡板安装高度h和挡板长度l3个结构参数的均值和标准差。

结构变量不确定性信息如表1所示。

表1 结构变量不确定性信息

各不确定性结构变量的分布参数之一(均值)也是个不确定性变量，分布参数不确定性信息如表2所示。

通过CFD仿真计算可得出不同封头结构下，封头每个出口处的质量流率qi，采用质量流率qi的标准差S表示封头出口处质量流量分配的均匀性。不均匀度S值越小，进入各层翅片的流体流量分配越均匀，翅片区域的换热效率越高。

因此，以不均匀度S最小为设计目标，其表达式如下(为了简化后面构建数学代理模型，本文计算将输出得到的标准差统一放大105倍):

(1)

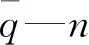
2 自适应Kriging代理模型构建

2.1 基于CFD仿真分析的封头采样点获取

挡板孔径d、挡板安装高度h和挡板长度l分别取分布均匀的5个水平，按照L25(53)正交表生成初步试验方案；为验证后续近似模型的准确度，笔者随机选择25组样本中的5组数据作为误差分析样本，这样由20组试验样本数据构建初始的代理模型，由剩下的5组样本数据检验初始模型的准确度。

换热器封头结构的试验方案如表3所示。

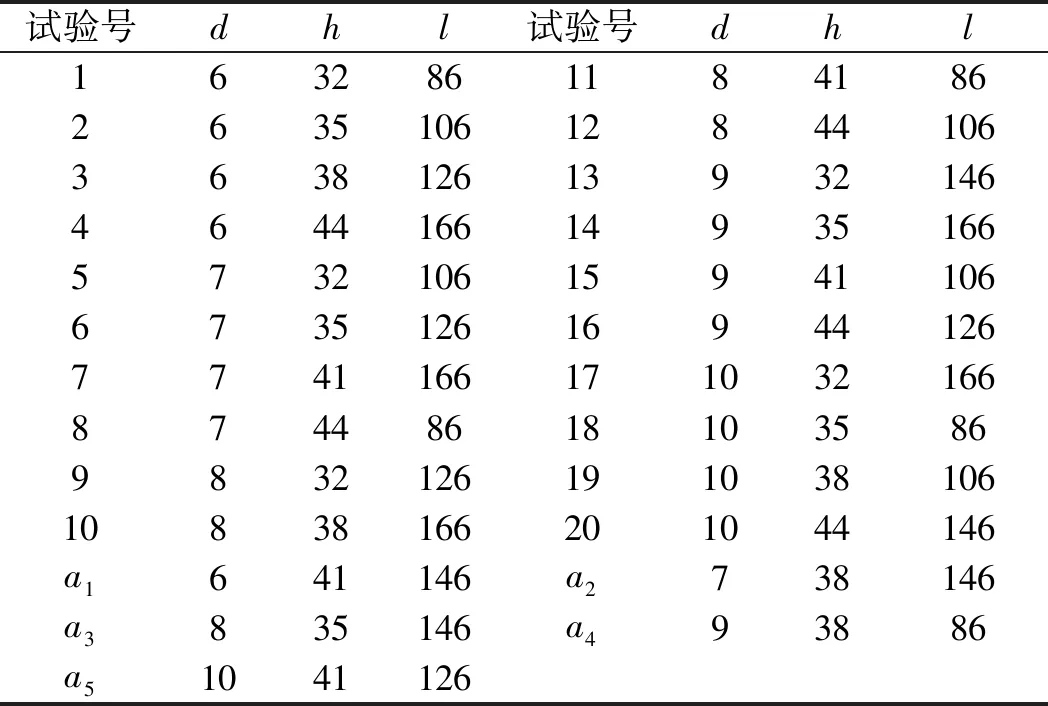
表3 换热器封头结构的试验方案

笔者基于以上25组试验设计点采样，进行打孔挡板封头内部流体仿真分析。第5实验组的封头内部流体速度分布云图如图2所示。

图2 第5实验组的封头内部流体速度分布云图

图2中，来自封头入口管道的流体，经过挡板分流，使得流速分布趋于均匀，有效减弱了射流区对封头的冲蚀；大流量的流体先进去封头腔体冲击挡板得到缓冲，然后进入到打孔挡板封头的11个出口通道。经过挡板对流场的重新分配，使流体流速分布逐步趋于均匀，换热器换热效果良好。

笔者按照封头结构的试验方案修改模型，划分网格并进行仿真计算，读取进出口的质量流率。

各采样点处不均匀度S计算结果如表4所示。

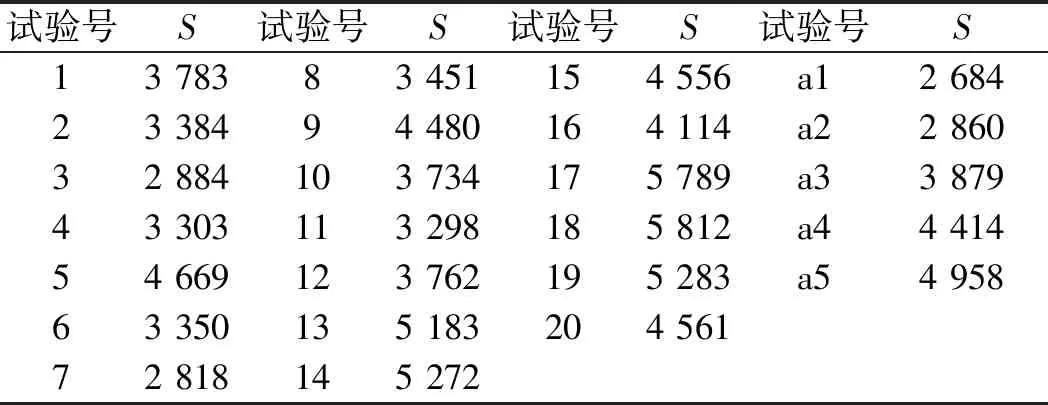
表4 各采样点处不均匀度S计算结果

2.2 初始Kriging代理模型的构建

笔者利用MATLAB软件中的Dace工具箱建立初始的Kriging代理模型，根据Fluent仿真分析获取的25组模型采样数据，计算不同孔径d、挡板安装高度h和挡板长度l对应的流体不均匀度S的预测均值以及预测方差；构建的初始Kriging模型的最大均方根在1.5×10-4左右。

为了充分验证最终模型的准确性，笔者同时将采样数据导入Isight软件，将前20组样本点利用“Approximation Models”模块生成近似模型；选用R2作为评判标准，R2越接近1预测模型的可信度越高，以5组样本点a1～a5用作误差分析，计算得到R2=0.943。

2.3 基于预测区间准则和遗传算法的Kriging代理模型优化

初始代理模型构建完成后，需要增加样本点以更新模型，提高Kriging代理模型的精度。笔者基于预测区间最大化准则和遗传算法相结合的方法，对封头初始模型进行优化。

优化步骤主要分为：

(1)根据初始模型的性能预测均值YS，采用基于遗传算法和非线性规划的函数寻优算法进行求解。非线性寻优利用当前染色体值采用函数“fmincon”寻找目标函数的局部最优值；遗传算法相关参数设置为：种群规模为100、最大进化代数为30、3个设计变量的字串长度均为1、交叉概率为0.6、最终变异概率为0.01。当种群进化到30代时，封头流量不均匀度S收敛到2 130，计算得到的最优输入变量值分别为d=6 mm，h=39.9 mm，l=166 mm；

(2)新增采样点的获取。基于预测区间最大化准则分别获取第k+1个采样点dk+1、hk+1和lk+1，并且在新的k+1个采样点处计算新的标准差Γk+1。

第k个采样点的模型和k+1个采样点两个模型之间的误差函数记为：

(2)

式中：H—模型误差；Γk—前k个采样点构建的近似模型的标准差；Γk+1—k+1个采样点构建的近似模型的标准差。

当两次采样更新的代理模型误差函数的期望值低于设定值ε=0.001时，迭代终止；

在初始Kriging模型基础上，笔者在迭代中逐步增加新的样本点来提高模型的拟合精度。

封头最终Kriging代理模型如图3所示(包括56组采样点)。

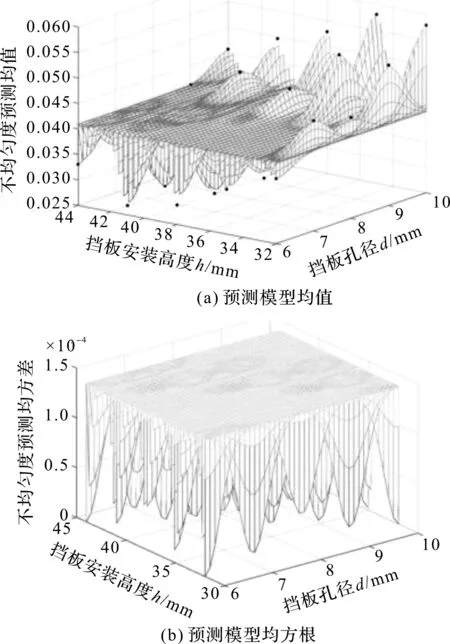
图3 封头最终Kriging代理模型

随着新的采样点的增加，可见最终的代理模型流体不均匀度S的最大均方误差已经小于0.8×10-4，证明构建的封头Kriging代理模型可以代替封头的真实模型，可进行后续结构不确定性优化设计；

同时，为了进一步验证代理模型的有效性，笔者将这56组采样数据导入Isight；其中，选取46组采样点重新构建Kriging模型，剩下10组采样点进行误差分析；

依然选用R2作为评判标准，计算得到R2=0.971，比初始Kriging模型的R2=0.943更接近于1。因此，笔者将这个代理模型作为最终优化的Kriging代理模型。

3 基于Isight的换热器封头结构不确定性优化设计

3.1 不确定性优化设计流程

本文先确定出各个设计变量的取值范围，通过L25(35)正交表生成25组试验方案，构建Kriging初始代理模型，后经过非线性规划遗传算法和预测区间准则方法增加新的样本点，最终获得56组样本数据，将这些样本点数据整理成规范的文本文档，导入Isight优化软件，进行封头结构参数尺寸的优化选择；利用Isight中“Optimization”模块的NLPQL梯度优化算法进行优化选择。

NLPQL算法将目标函数以二阶泰勒级数展开，并把约束条件线性化，通过求解二次规划得到下一个设计点，然后根据两个可供选择的优化函数执行一次线性搜索；其中，Hessian矩阵由BFGS公式更新。

具体的优化流程如下：

首先将“Approximation Models”模块的信息传递到“Optimization”模块，选择NLPQL算法并保持默认配置参数；然后设置输入变量的上下限和优化目标，将封头优化问题用以下的线性规划模型表示：

Min S

s.t.dmin≤d≤dmax

hmin≤h≤hmax

lmin≤l≤lmax

(3)

式中：S—不均匀度；d，dmin，dmax—孔径的设计值、最小值和最大值；h，hmin，hmax—挡板安装高度的设计值、最小值和最大值；l，lmin，lmax—挡板长度的设计值、最小值和最大值。

输入变量为封头结构尺寸d、h和l，优化目标为封头流体分配不均匀度S最小，运行优化模块得出最优结果。

封头结构尺寸优化流程如图4所示。

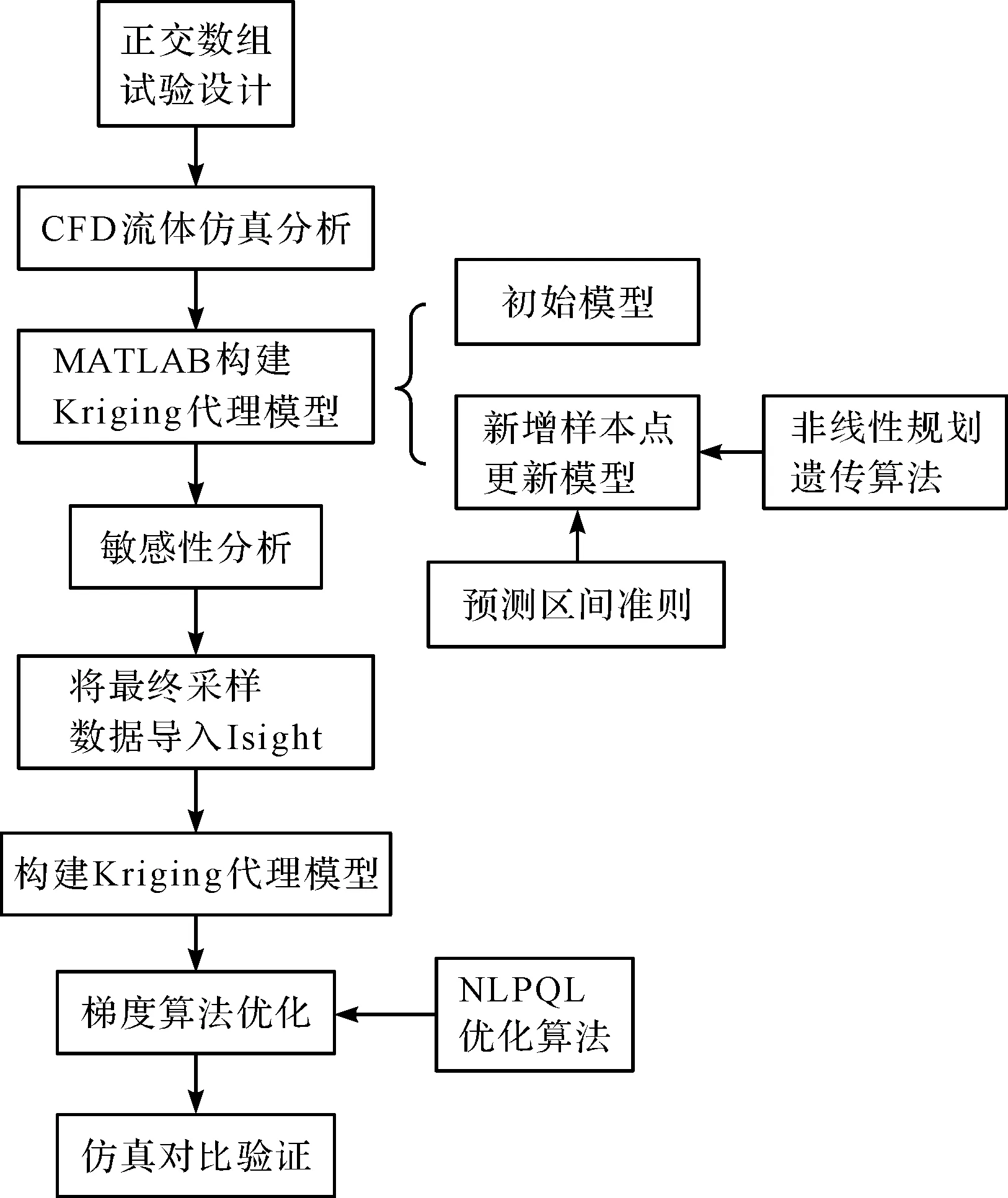
图4 封头结构尺寸优化流程

3.2 试验及结果分析

经过49次迭代计算后，当孔径d=6.742 7 mm，挡板安装高度h=39.361 mm，挡板长度l=146.8 mm时，打孔挡板封头具有最佳分配效果，其流体分配不均匀度为S=0.025 30。

笔者对优化结果中的封头结构参数尺寸进行处理，取孔径为6.74 mm，挡板安装高度为39.36 mm，挡板长度为146.8 mm，挡板孔间距5.75 mm。

最佳打孔挡板封头结构的二维尺寸如图5所示。

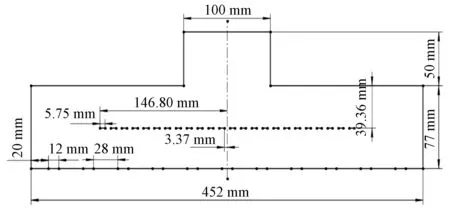
图5 最佳打孔挡板封头结构的二维尺寸

最佳尺寸的打孔挡板封头流体速度云图如图6所示。

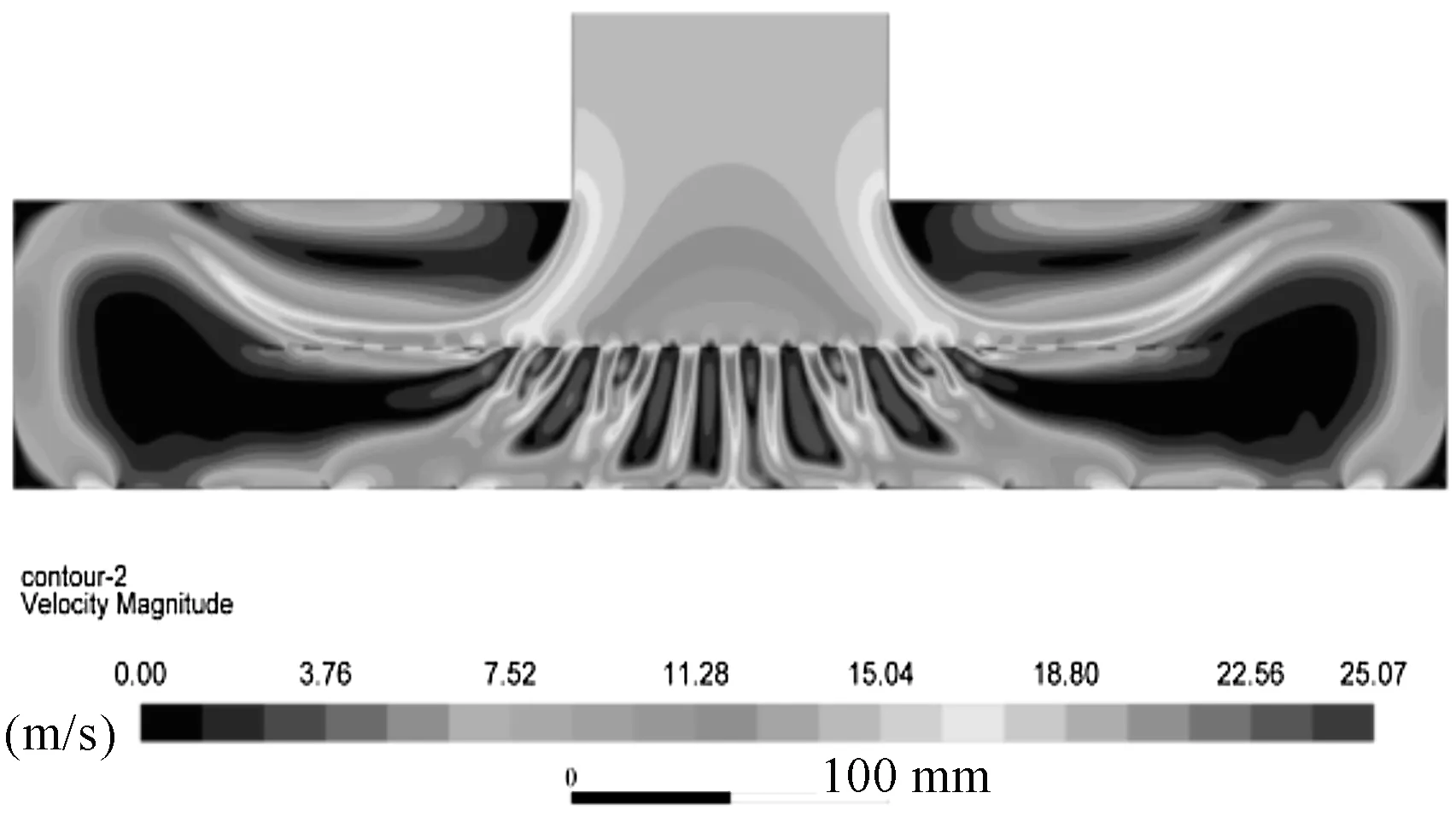
图6 最佳尺寸的打孔挡板封头流体速度云图

图6中，计算得到的封头流体分配不均匀度S=0.025 16。

综上可知：由仿真确定的最佳封头的不均匀度值与优化结果的预测值S=0.025 30极其相近；同时由速度云图可知，封头出口速度比较均匀；由此验证了本文优化方法的有效性以及优化结果的准确性。

4 结束语

本研究提出了考虑分布参数不确定性的换热器封头结构优化设计方法；首先确定了打孔挡板封头的孔径、挡板安装高度、挡板长度等结构变量，及其分布参数的不确定性表达函数；其次基于预测区间准则和遗传算法，建立了翅片结构变量与流动不均匀性的高精度Kriging近似模型；最后构建了面向流动不均匀度最低的封头结构变量不确定性优化设计函数，在Isight中建立了优化仿真程序，实现了封头结构变量的优化设计。

CFD仿真结果表明，经优化后封头出口速度更均匀，由此验证了方法的有效性以及优化结果的准确性。