高斯型径向基函数的切比雪夫配点法
郭玄玄,王福章
(淮北师范大学 数学科学学院,安徽 淮北 235000)
高斯型径向基函数方法属于配点型无网格法,该法相对于基于网格划分的传统有限元法,仅需区域配点信息即可对所求问题进行数值模拟,具有无需网格划分、原理简单、易编程和谱收敛性等优点[1-4].高斯型径向基函数方法的特点在于直接借助于1 组区域离散点作为配点来构造微分方程边值问题数值解的近似函数,近年来吸引了许多数学界和力学界专家进行深入研究.
目前,对高斯型径向基函数的研究比较多.张志雄等[5]用Gaussian 径向基函数对多个标志点的图像配准来解决图像局部弹性变换问题;John等[6]用Gaussian 径向基函数求近似导数和微分方程;黎鸣[7]用Gaussian 径向基函数网络建立潜在剖面模型;袁桂霞等[8]提出了一种基于 Gaussian径向基函数的复制-移动篡改检测算法;柳丹等[9]提出了基于Gaussian 径向基的子区域优化温度场重建算法;孔宪仁等[10]用改进Gaussian 径向基函数响应面方法修正蜂窝板模型;Zheng 等[11]用Gaussian 径向基函数研究了地下水的非稳定流问题.尽管高斯型径向基函数在实际问题的数值模拟中应用比较多,但针对高斯型径向基函数精度的改进工作却鲜见报道.
本文考虑椭圆型偏微分方程边值问题,在数值模拟过程中,利用切比雪夫节点代替传统的均匀配点,与传统高斯型径向基函数方法和理论解的结果进行对比研究,并分析了基于切比雪夫节点的高斯型径向基函数对椭圆型偏微分方程边值问题的数值结果的影响.
1 高斯型径向基函数配点法
为了简要说明高斯型径向基函数配点法的基本思路,以二维平面区域2Ω ⊂R 上的椭圆型偏微分方程的边值问题为例,即
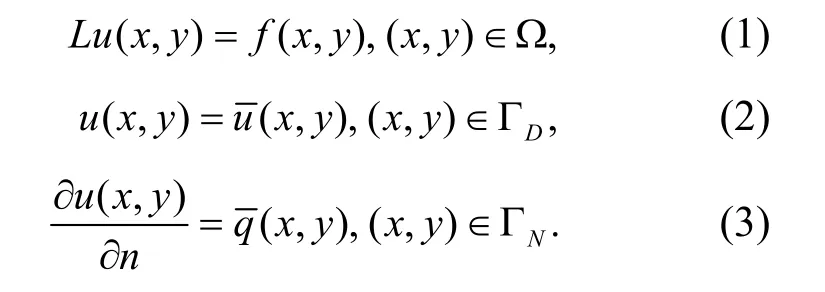

2 切比雪夫配点
众所周知,传统的高斯型径向基函数配点法在数值模拟过程中所用的配点采用的是所考虑物理区域中的均匀布点,如图1 所示.

图1 传统均匀布点
为了改进传统配点型无网格法的数值模拟精度,本文引入了切比雪夫配点法,其基本思路是引入定义在区间( -1, 1)上的切比雪夫节点作为计算过程中的配点,增加区间端点 -1 和1,构成闭区间[ -1, 1]的配点,具体如图2 所示.

对任意区间[ a , b] ,可用式(7)进行仿射变换.


图2 切比雪夫节点
3 数值求解

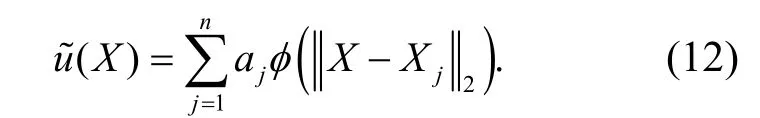
进一步地,对应点处的法向数值解可由式(12)求法向导数得到.
4 算例分析
为便于研究,笔者进行了大量数值实验,本文以下述椭圆型偏微分方程边值问题为例:

传统配点型无网格方法选取的均匀边界配点数N =609,因为切比雪夫节点生成的配点是非均匀分布的,所以只能选取与均匀分布近似的配点数N =616,但所考虑计算点总数相同,均为40 401 个.均匀配点数值模拟误差如图3 所示.
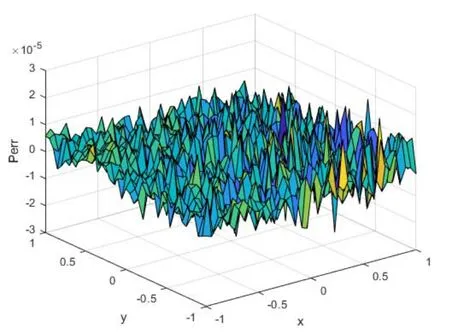
图3 基于均匀配点的高斯型径向基函数所得计算误差
图3 表明,点( -1, 1)和(1, 1)附近的误差较大,而其他点处的误差非常小,所有计算点处的平均相对误差为 Perr= 3.99 × 10-6.切比雪夫配点法所得误差如图4 所示.
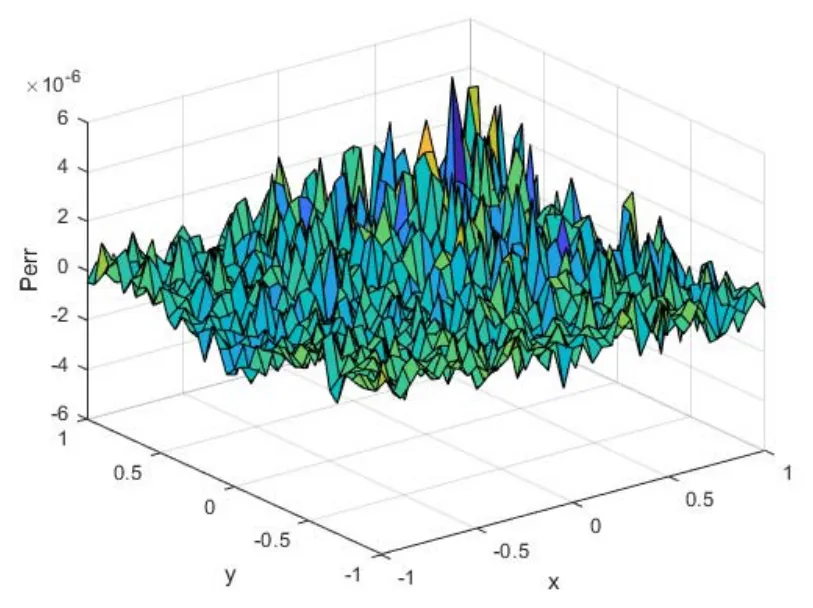
图4 基于非均匀配点法所得计算误差
图 4 表明,点( -1, 1)和(1, 1)附近的误差仍然较大,但比传统高斯型径向基函数的计算结果提高了精度,所有计算点处的平均相对误差为Perr= 3.43 × 10-7.综上,传统的高斯型径向基函数法在所考虑物理区域边界角点附近数值模拟精度较低,基于切比雪夫节点的径向基函数配点法不仅可在边界处提高计算精度,还提高了所有物理区域上的计算精度.
5 结论
为了提高高斯型径向基函数法数值模拟偏微分方程边值问题的精度,本文给出一种将传统径向基函数配点法和切比雪夫节点相结合的数值方法,对椭圆型微分方程的边值问题进行了高精度数值模拟.在 Matlab 工具中的数值模拟实验表明,切比雪夫节点结合高斯型径向基函数的方法能得到更精确的计算结果,且其误差明显减小.

