考虑弃风成本和深度调峰成本的弃风临界值计算

蔡振华，李立雄

(1. 湖南城市学院 机械与电气工程学院，湖南 益阳 413000；2. 智慧城市能源感知与边缘计算湖南省重点实验室，湖南 益阳 413000)

现代电力系统中，电力调峰的电源种类繁多，2018 年，国内累计总发电量7 111.8 TWh，其中火电机组发电量占总发电量的 66.5%；新能源发电总量为634.2 TWh，风电机组发电量占新能源发电总量的 57.7%[1].在传统发电与新能源协同调峰的过程中，火电机组与风电机组分别在各自电源种类中的占比最大，因此，在调峰经济性研究中，考虑两者的协同调峰效应具有重要意义.

风电机组装机容量大规模增加的同时，也带来了许多问题.风电波动性、间歇性和逆调峰特性，使得现有火电机组的调峰难以满足要求.如：当风电处于最大出力阶段时，系统管理人员为了最大限度地利用低成本风电，选择将火电机组停机.该方法虽能降低火电机组的发电成本，却忽略了较大程度地依赖风力发电，其随机性可能导致大规模的系统停电事故，给系统的安全运行带来了较大的风险.因此，采用风电机组与火电机组协同调峰的调度方式在兼顾节省调度成本和增加供电可靠性方面无疑是最佳选择.

根据节能调度规定[2]，电网公司应根据各类火电机组的技术经济特点，按照系统的电力电量平衡需求，优先安排发电成本低、调节能力好的火电机组发电，同时避免常规火电机组的频繁启停，使其尽量高效运行.此项规定使得系统检修人员在已有火电机组装机容量的基础上，不断改造机组，增加火电机组的发电能力，即对火电机组进行灵活性改造，使得机组具备深度调峰能力，以此减少火电机组的启停成本.

火电机组的深度调峰要求灵活性改造后的机组仍然具有低于其常规最小出力的运行能力，一般可分为稳燃不投油深度调峰和投油深度调峰 2种.深度调峰运行阶段的成本除了包含运行煤耗成本外，还包含其他附加成本.例如：稳燃不投油深度调峰成本包括机组损耗成本，而投油深度调峰成本除了机组损耗成本外，还包括投油损耗成本和环境成本.由于深度调峰成本呈现非线性特征，为了研究方便，工程人员常根据相关的线性化理论将机组的深度调峰成本划分为不同的档次，即将深度调峰阶段的成本经线性化处理为机组出力与相应单位调峰成本的乘积形式.为简化计算，本文采用同样的计算方式.

一般来说，制定短期发电调度计划以日内负荷曲线为主，考虑风电在内的负荷曲线通常采用等效负荷曲线.等效负荷曲线是指负荷曲线减去相应时段的风电出力曲线得到的等值曲线.当系统的常规调峰最小出力高于等效负荷曲线时，系统为了有效利用“低成本”风电，避免大规模弃风，火电机组将运行于深度调峰状态.文献[3]针对风电出力的不确定性，采用情景削减技术，降低了调峰运行计算的复杂性.文献[4]在电源侧深度调峰的基础上，提出调峰出力率与调峰成本 2个新指标来评估省级电网的调峰形势.文献[5]考虑火电机组的灵活性改造，以 Benders 分解算法求解调度问题，算例表明所构建的模型能在提升电力系统经济性的同时促进风电的消纳.文献[6]提出一种调峰分摊补偿方法，采用K-means 方法对机组进行合理分类并进行分摊，引入调峰能力实现系数并进行修正，结果表明建立的模型能激励更多的机组参与调峰服务.文献[7]提出一种考虑调峰约束的评估风电消纳能力方法，并给出促进风电消纳的相关建议，该方法及建议对电力部门相关政策的制定具有重要的实际意义.文献[8]在市场机制下建立考虑深度调峰的市场出清模型，实现低谷时段火电与可再生能源的发电权交易，将难以解决的爬坡约束考虑在内.文献[9]提出改进等效电量函数法，克服传统方法中易丢失时序信息的缺点，成功求解了辅助新能源与常规能源协调规划的问题，并进一步提出2 个描述调峰性能的指标.文献[10]针对风电并网时调峰能力的不足，提出采用以 WSR 系统方法论对用户参与风电并网调峰进行研究的方法，建立了合理的系统模型.

虽然已有不少有关深度调峰问题的研究，但现实中的深度调峰成本与风电弃风成本的协同优化，以及最优弃风量计算的问题仍有待解决.本文旨在构建以常规调峰成本、深度调峰成本和弃风成本的总和最小为目标的机组组合综合优化调度模型，并对一个10 机测试系统进行求解，与已有的各种模型算例结果进行比较，以验证所提出模型的有效性和实用性.

1 综合优化模型关键指标

1.1 常规调峰最小出力

系统常规调峰最小出力是区分火电机组常规调峰和深度调峰的重要指标，在综合模型求解过程中，常规调峰最小出力取系统内所有火电机组出力的最小值之和.在系统调峰过程中，不同调峰能力的机组将采取不一样的调峰措施以满足系统成本经济性需求.当某时段的等效负荷低于常规调峰最小出力，不具备深度调峰能力的部分机组，将采取直接停机方案；而具备深度调峰能力的火电机组，首先在深度调峰区段进行负荷分配，若该分配方案仍低于最低深度调峰机组的调峰下限值，则该机组才采取停机方案.采取这类调峰措施的主要原因是火电机组的深度调峰成本较机组的开停机成本更加经济.

1.2 非常规调峰容量

任何时段，若存在系统常规调峰容量下限大于净负荷，则非常规调峰负荷为常规调峰裕度的绝对值；否则，非常规调峰负荷为0.

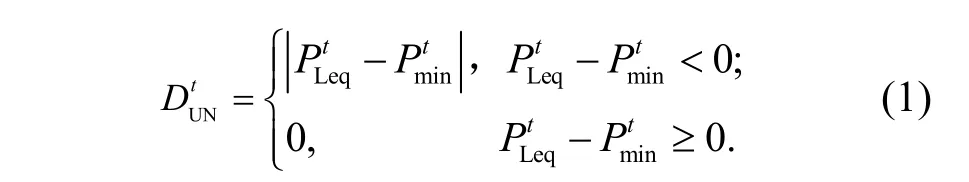
在实际工程中，还需考虑含风电机组系统的调峰平衡情况，其相关调峰指标和调峰曲线如图1 所示.由图1 可知，要使等效负荷曲线位于最小出力之上，避免增加开停机成本，一方面可以将常规调峰最小出力往下平移，即可以对相关机组进行灵活性改造，增加机组的深度调峰能力来平衡负荷；另一方面，可以采用弃风的方法，减少风电机组的出力，使得等效负荷曲线向上平移来平衡负荷.

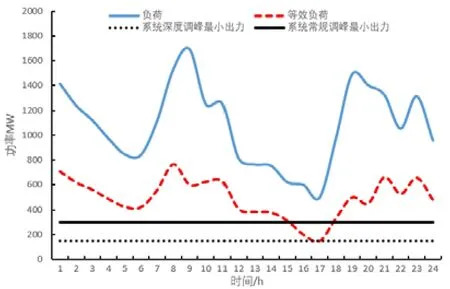
图1 系统调峰曲线

2 机组组合综合优化模型

传统机组组合问题的求解是经典优化调度模型的典型代表，它是指在满足负荷、爬坡等约束条件下，合理安排机组的开/停机顺序与出力，以使系统发电成本最小.该问题的主要求解过程包括开/停机方案求解和最优负荷分配方案求解2个方面.最优负荷分配方案一般是以等微增率准则来确定火电机组的出力，在传统调度方式下，未考虑到风电并网引起的弃风成本问题和深度调峰带来的隐形效益，因此经典调度模型的求解有较大的局限性.为了将深度调峰成本和弃风成本考虑在内，本文建立了如式(2)的综合优化模型.

若只考虑式(2)的第1 项，不计及机组的深度调峰能力，同时考虑风电完全消纳，则建立的模型为常规调度模型.

若考虑式(2)的第1 项和第2 项，计及机组的深度调峰能力，即将机组的单位深度调峰成本考虑在内，且考虑风电完全消纳，则所建立的模型为未弃风深度调峰调度模型.该模型表示当系统等效负荷低于式(1)中已开机机组的可调节容量下限时，机组仍然不停机，维持在机组深度阶段运行，直至系统负荷低于部分机组深度调峰下限时，这些机组才采用停机方案.该模型表明机组能运行在深度调峰阶段，可有效减少机组的停机成本和开机成本.

若考虑式(2)的第1 项和第2 项，计及机组的深度调峰能力，但考虑完全弃风，则所建立的模型为全弃风条件下的深度调峰调度模型.该模型虽然能有效利用火电机组可控的调峰能力，避免风电出力的波动性和间歇性引起系统频率变化等问题，却未能利用风电的低成本特性.

若将式(2)的第1 项、第2 项和第3 项均考虑在内，即建立考虑弃风成本和深度调峰成本的综合优化模型，此时，因模型综合考虑了弃风所引起的弃风成本和深度调峰所产生的成本，所以能合理利用低成本的风力发电.在该模型中，若考虑风电利用率低的情况，系统弃风越多，弃风成本就越高，从而会产生较高的综合运行成本；若风电利用率较高，系统弃风越少，但为了满足系统等效负荷的需求，火力发电成本也会越高，总的综合运行成本也就越高.因此，该模型的求解存在一个使得综合模型的成本最优和弃风量最优的折中解.显然，该问题的求解对系统调度人员的决策具有重要的实际意义.

3 算例分析

为了验证本文所提模型的有效性，测试系统的机组数目N 取10，机组进行灵活性改造前的具体参数见文献[11].为与国内机组情况一致，10个机组参数中的量纲进行了换算，机组爬坡率取相应机组最大出力的 3%，预留的调峰上备用容量按尖峰负荷的10%考虑.考虑到机组灵活性改造的效益问题，本文对所有机组的容量进行了改造，为了简化计算，并未考虑机组灵活性改造的前期投资成本.机组的深度调峰容量和调峰成本如表1 所示.

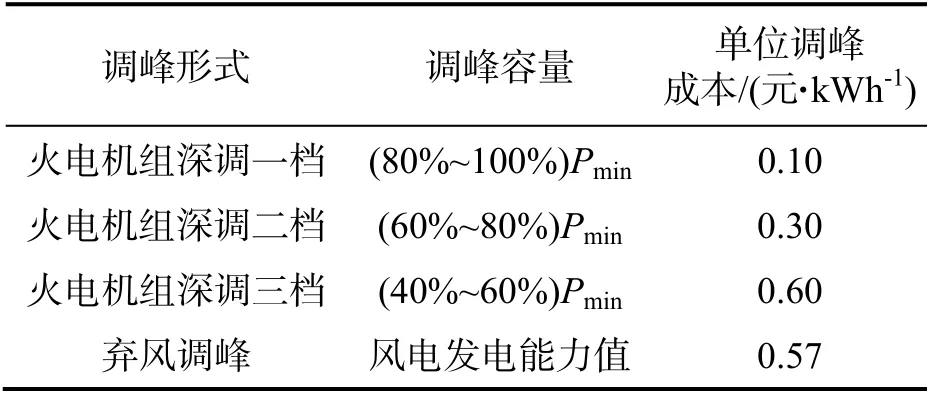
表1 深度调峰容量和调峰成本

测试系统的调度周期T 取24 h，每1 h 设为一个调度时间段，系统24 h 负荷值和风电最大发电能力值分别如表2～表3 所示.

表2 系统24 h 负荷值

系统负荷值与相应时刻风电出力预测值之差为系统净负荷值.系统常规最小出力取 10 个机组最小出力之和，即440 MW.当系统等效负荷值与系统常规最小出力之差为正时，属于常规调峰阶段；当该差值为负时，可以采用非常规调峰方法或常规调峰的停机方式处理.系统非常规调峰裕度值如表4 所示.

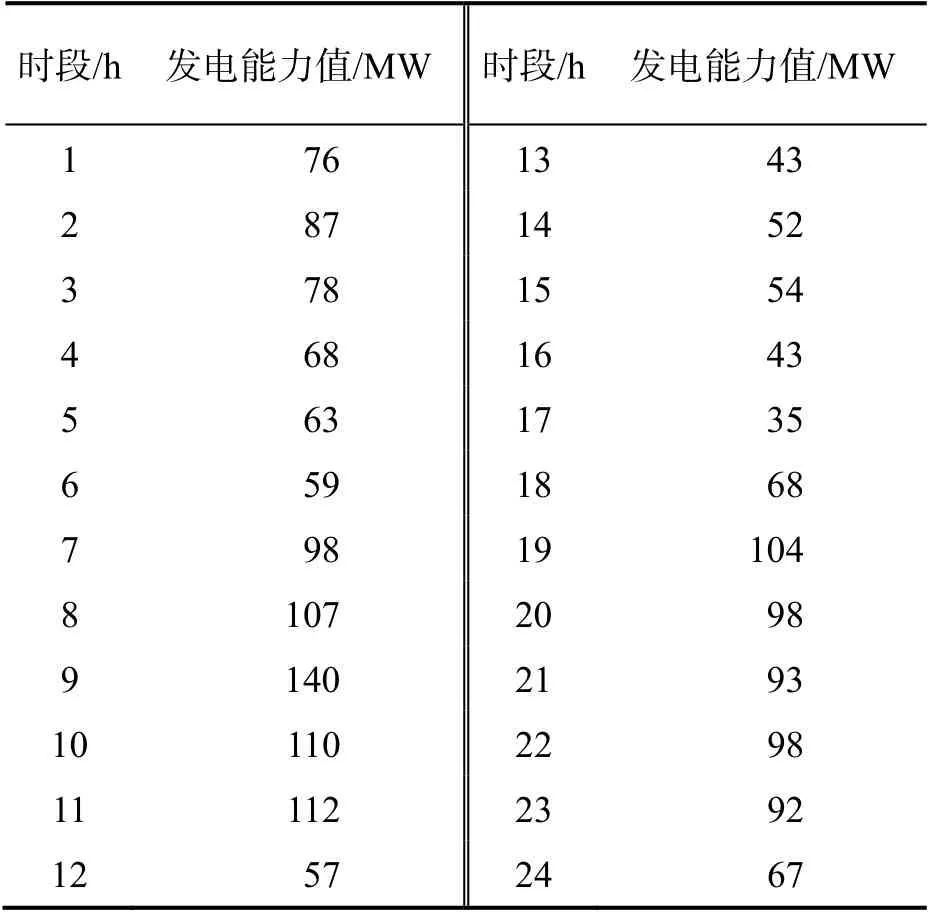
表3 24 h 风电最大发电能力值

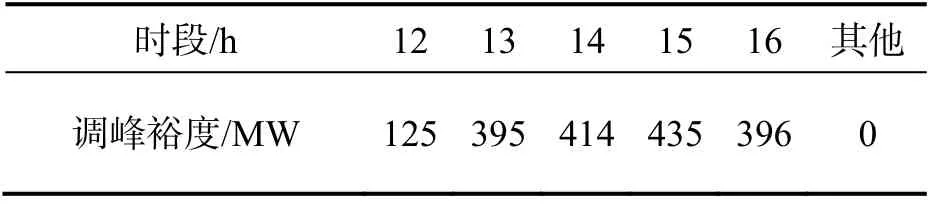
表4 系统非常规调峰裕度

考虑到问题求解的复杂性，为了简化求解该混合整数非线性规划问题，本文采用Yalmip 工具箱并调用Cplex 软件，分别对机组常规调度模型、未弃风深度调峰调度模型和全弃风深度调峰调度模型进行求解，最后求得的最优成本和相应弃风量如表5 所示，各模型下12～16 h 的弃风量和相应弃风成本如表6 所示.

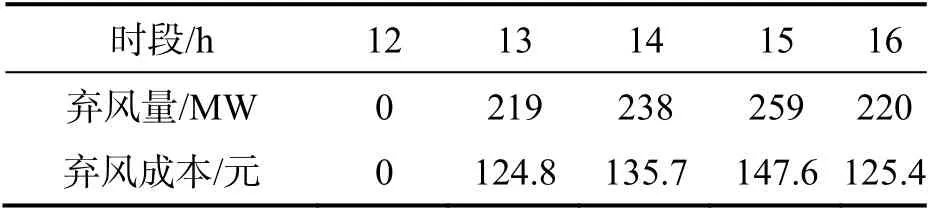
表5 最优弃风量和弃风成本

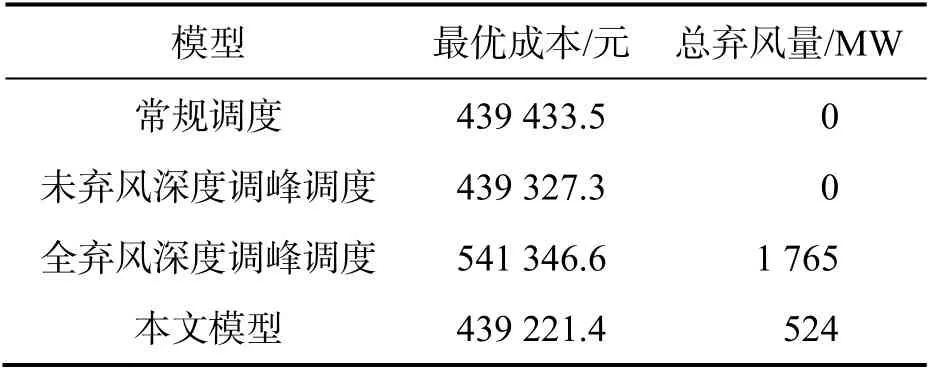
表6 各模型求解结果对比

由表6 可知，本文所建模型较常规调度模型的最优成本降低了 212.1 元，这主要是由于深度调峰较常规调峰更有利于节省成本.同时，本文模型较未弃风深度调峰调度模型和全弃风深度调峰调度模型的最优成本也分别降低了 105.9 元和102 125.2 元.导致成本降低的主要原因是：1)本文模型的单位弃风成本在深度调峰成本的二档和三档之间，首先采用一、二档深度调峰相对于弃风更有利于节省成本；2)全弃风深度调峰调度模型的系统负荷值较本文模型的等效负荷值大，这会导致其成本增加.因此，在考虑调峰时，应综合考虑调峰成本与弃风成本的影响.

通过本文模型计算出的一个调度周期内的综合弃风临界值为53.03%，即在本文所给基础数据的前提下，将936 MW(各时段最优弃风量见表5)的风电弃除更为合理.对火力发电厂而言，仅考虑非常规调峰裕度大于176 MW 时段，若平均调峰深度大于 42.9%，采用弃风方案有利于节省成本；反之，则采用深度调峰方案更具经济性.

4 结语

为了有效利用火电机组的深度调峰能力，本文综合考虑弃风成本和深度调峰成本，建立了机组组合综合优化调度模型，并分别对常规调度模型、未弃风深度调峰调度模型和全弃风深度调峰调度模型进行求解.结果表明，本文所建模型能有效降低调度周期内的调峰成本.此外，该模型下的最优弃风临界值求解结果表明：当非常规调峰裕度值高于该时段的弃风临界值时，高于临界值的部分功率采用弃风调峰，低于临界值的部分功率采用深度调峰，更有利于节省成本；而非常规调峰裕度值低于该时段的弃风临界值时，采用深度调峰更有利于节省成本.