公路弯道横断面超高值的理论推导

肖 明

(湖南城市学院 土木工程学院，湖南 益阳 413000)

公路弯道中，为了抵消汽车在圆曲线上行驶时产生的离心力，设计时将弯道部分的横断面做成外侧高、内侧低的单向横坡形式，称为超高.超高数值和超高渐变率的选取将影响行车的安全和舒适性.国内外对超高的研究比较多，孙爱民等[1]从原理上对超高过程进行了说明，设计过程中要考虑安全、经济、美学等因素；毛爱民[2]建立了圆曲线半径和超高横坡值ih的二次抛物线关系式，分析了平曲线超高横坡 ih、横向力系数 μ与安全性、舒适性的关系，提出了几点超高设计的建议；邵毅明等[3]以“路-人-车”仿真模型为手段，以超高率p 和行驶速度v 为试验变量，通过仿真试验，得到了超高对汽车转弯操舵矩和侧倾摆动的影响；熊峰等[4]研究了中美两国规范在平曲线超高方式上的特点，对目前国内超高缓和段设置方法的适用性做出了评价，并对其提出了改善建议；王磊[5]，杨永前等[6]以S 形曲线路段为例，详细分析了S 形曲线上超高过渡的过程，优化了S 形曲线的设置；刘琦[7]研究了纵坡对超高横坡的影响，讨论了纵坡、超高渐变率与排水不良路段长度的关系；张航等[8]构造可靠度函数，讨论了车速v、曲线半径R、横向力系数μ 与超高可靠性的关系.总体而言，宏观角度的超高研究较多，而具体的超高设计过程讨论较少.本文从超高值的理论公式推导出发，对超高过程中各桩号超高值的计算进行了研究，全面地展示了超高设计的过程.

1 超高旋转方式

根据公路超高特点，现代公路线形设计的无中央分隔带超高过渡方式归纳起来有 3 种(假定路线为左转弯)：绕路面内侧硬路肩边缘旋转进行超高过渡；绕路面中线旋转进行超高过渡；绕路面外侧硬路肩边缘旋转进行超高过渡，见图1.

图1 无中央分隔带公路超高过渡方式

有中央分隔带公路的超高过渡方式归纳起来同样有 3 种(假定路线为左转弯)：绕中央分隔带外侧边缘旋转进行超高过渡；绕中央分隔带中心旋转进行超高过渡；绕各自行车道中心旋转进行超高过渡，见图2.

图2 有中央分隔带公路超高过渡方式

本文主要推导无中央分隔带公路绕内侧边线和有中央分隔带公路绕中分带边缘旋转的超高计算公式.

2 无中央分隔带公路绕路面内侧边缘旋转超高值计算

图3 绕路面内侧边缘超高旋转过程3D 示意

为了更清晰地体现各几何量之间的关系，建立路面超高计算模型，见图 3.其中，hx，h′x和 h″x分别代表距直缓点(ZH 点)x 距离处，外侧路基边缘、中线、内侧路基边缘与设计高程(路基边缘定义为设计高程点)的差；B 为路面宽(含硬路肩)，bJ为土路肩宽度，b 为加宽值；ZH 和HY 分别代表直缓点和缓圆点；iG为路拱横坡，iJ为土路肩横坡；l0为由土路肩横坡iJ旋转到路拱横坡iG的提肩段，长度为1 m(此时，超高渐变率为1%)；x为超高计算任意位置距直缓点的距离，x0为外侧路面超高由-iG旋转为 iG时的过渡长度；Lc为超高过渡段长度；ih为圆曲线超高横坡，ix为任意位置的横断面超高值.

2.1 圆曲线段超高值

当超高位置位于圆曲线上时，提取圆曲线段的横断面图，见图4.其中，N1(路基边缘)为超高设计基准点；N2为超高旋转轴的位置.

图4 圆曲线段横断面

根据几何关系得到路基外缘、中线、内缘的圆曲线段超高值：

汇总超高值如表1 所示.

表1 无中间带公路圆曲线段超高值

2.2 过渡段超高值

超高过渡绕路面内侧边缘旋转时，首先，将外侧绕中线抬高到与内侧相同坡度；然后，再绕内侧硬路肩边缘旋转.当超高位置位于过渡段上时，调整图3 视角到前半部分，当计算x≤x0外缘、中线、内缘的超高值时，分别采用图5～图7 进行计算；当计算x＞x0外缘、中线、内缘的超高值时，分别采用图8～图10 进行计算.

图5 位于过渡段上时外缘超高计算示意(x≤x0)

图6 位于过渡段上时中线超高计算示意(x≤x0)

图7 位于过渡段上时内缘超高计算示意(x≤x0)

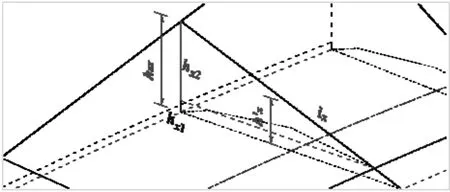
图8 位于过渡段上时外缘超高计算示意(x＞x0)

汇总超高值如表2 所示.

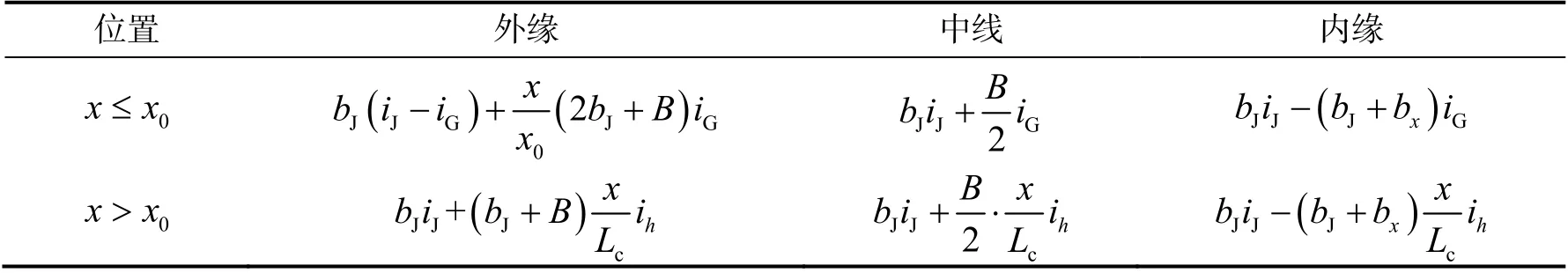
表2 无中间带公路过渡段超高值

从以上分析中可以发现：内缘的超高值和路面宽度没有关系；超高值和路面宽度正相关.

3 绕中央分隔带外侧边缘旋转超高值计算

图11 绕中央分隔带边缘超高旋转过程3D 示意

图12 有中央分隔带公路标准横断面

对于有中央分隔带的公路，通常是指高速公路和一级公路，常用的超高方式为绕中央分隔带外侧边缘旋转.为了更清晰地体现各几何量之间的关系，建立路面超高计算模型和标准横断面图，见图11 和图12.其中，hCx和hFx分别代表距直缓点x 距离处标准横断面C 点和F 点的超高值；B 为路面宽，b1，b2为左右路缘带宽，bJ1为硬路肩宽，bJ2为土路肩宽；ZH 和HY 分别代表直缓点和缓圆点；iG为路拱横坡，iJ为土路肩横坡；l0为由土路肩横坡iJ旋转到路拱横坡iG的提肩段，长度1 m；x 为超高计算任意位置距直缓点的距离；Lc为超高过渡段长度；ih为圆曲线超高横坡，ix

为任意x 位置超高值；bx为x 位置路面加宽值.

3.1 外侧C 点超高值

外侧C 点超高值计算示意见图13.

图13 外侧C 点超高值计算示意

在纵向(行车方向)，根据外侧超高三角形比例关系，有

3.2 内侧F 点超高值

内侧F 点超高值计算示意见图14.

图14 内侧F 点超高值计算示意

在纵向(行车方向)，根据外侧超高三角形比例关系，有

由式(14)和式(15)得到

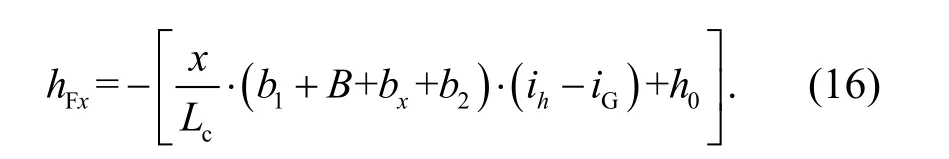
在横向(垂直行车方向)，根据断面三角形比例关系，F 点超高值为

内外侧F 点的超高值见表3.

表3 有中间带公路过渡段超高值

从表3 计算公式中可以发现，整个超高值和路面的宽度(含加宽值)成正比例的关系.

4 案例计算

4.1 工程概况

桃江县省道牛鸬线(S541)某弯道，设计速度40 km/h，路基宽8.5 m，路面宽7.0 m，土路肩宽0.75 m，路面和土路肩横坡分别为2%和3%.平曲线半径R 为220 m，缓和曲线LS为70 m，交点桩号为 K1+414.623，路线偏角 α 为 37°13′46.1″，弯道加宽值b 为0.8 m.

4.2 超高计算

依据《公路路线设计规范》[9]，对于一般地区公路设计，最大超高ih,max可取到8%，由半径(R)、超高(ih)和最大超高(ih,max)之间的关系，当设计速度为40 km/h、半径为220 m 时，超高值ih取4%.用表1 中公式计算的“理论值”与公路设计软件计算的“软件值”如表4 所示，两者大小基本相等.

5 结论

1)不同桩号超高值的大小和超高渐变率及超高过渡方式相关；

表4 弯道路基外缘、中线、路基内缘超高值

2)绕行车道边缘(含硬路肩)旋转的超高过渡方式，相对于其他超高过渡方式而言，在施工过程中，更容易控制路基和路面的设计标高；

3)对于较宽路面公路的设计，最大超高值不能取得过大，否则两侧路面高差较大，不利于路面排水和慢速车辆的行车安全，应充分考虑利用“部分横向力系数+超高”的方式来平衡车辆的离心力；

4)超高值的3D 计算图示，为公路设计人员正确理解超高过程提供了一个思路.