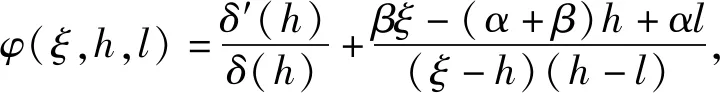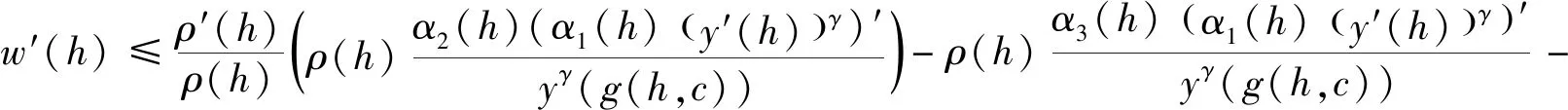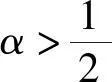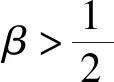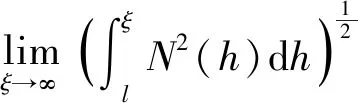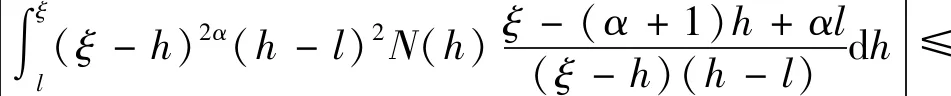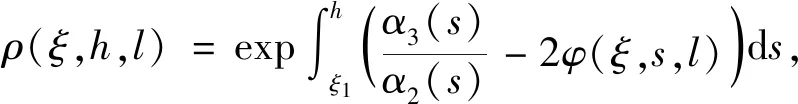具有阻尼和分布偏差变元的三阶中立型微分方程解的振动性与渐近性*
王雅坤, 孟凡伟
(曲阜师范大学数学科学学院,273165,山东省曲阜市)
0 引 言
本文研究了具有阻尼和分布偏差变元的三阶中立型微分方程解的振动性和渐近性质,其形式如下

(*)

本文中我们总有以下的假设成立:
(A1)ξ0>0是常数,+=(0,∞).
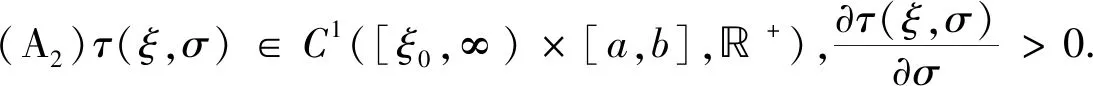
(A3)F(ξ,s,x)∈C([ξ0,∞)×[c,d]×(-∞,∞),),q(ξ,s)∈C([ξ0,∞)×[c,d],+),当x≠0时满足

(A5)η(s)∈C([c,d],)是严格增的,且方程(*)的积分是Riemann-Stieltijes积分.
我们关注Lx≥ξ0时,x∈C3[Lx,∞)具有性质α2(ξ)(α1(ξ)(y′(ξ))γ)′∈C1[Lx,∞)和α1(ξ)(y′(ξ))γ∈C2[Lx,∞)的方程(*)的解x(ξ). 并且解x(ξ)在L>Lx时,满足条件 sup{x(ξ):ξ≥L}>0. 通常情况下,若方程(*) 的非平凡解既不是最终为正也不是最终为负时,称为振动解,否则是非振动的. 如果一个方程的所有解都是振动的,则称其为振动方程.
1921年,Fite首次研究了具有偏差变元(DA)微分方程的振动性和非振动性[1],之后,这项工作迅速发展. 此外,微分方程的渐近性质也引起了学者们的广泛关注. 感兴趣的读者可以阅读文献[2-7]了解在何种条件下方程的解趋于0. 与此同时,时滞方程仍然是热门话题,读者可以阅读文献[8]第11章中有关时滞微分方程的应用.
随着工程和自然科学的发展,三阶中立型时滞(TOND)微分方程的振动结论被重视. 有关各种中立型时滞微分方程或者中立型时滞时标方程的研究越来越复杂化. 一般来说,系数的正则情况与非正则情况之间的差异会影响某些解的分类,并会根据不同的情形得到不同结果. 例如,文献[9,10]分别考虑了同一个方程的正则与非正则情况. 此外,丰富的方程类型使三阶中立型微分方程的研究更加有趣. 中立项可以分为线性项的,非线性项的(如文献[11]),分布项的(如文献[6,7,10]),方程还可以是混合变元的(如文献[12,13])或有阻尼项的(如文献[6,14])等.
我们的启发来自Senel和Utku[2]研究的三阶中立时标方程
Yang[14]考虑在y(ξ)=x(ξ)+B(ξ)g(x(τ))时的三阶时标方程
{r(ξ)φ([a(ξ)y△(ξ)]△)}△+b(ξ)φ([a(ξ)y△(ξ)]△)+P(ξ)F(φ(x[δ(ξ)])=0.
Martin Bohner[15]研究的三阶非线性阻尼时滞微分方程
(α2(ξ)(α1(ξ)(x′(ξ))γ)′)′+p(ξ)(x′(ξ))γ+q(ξ)f(x(g(ξ)))=0.


我们目标是在正则条件下得到具有DDA和阻尼TOND微分方程的新的振动判据,其研究方法来源于Meng和Xu[16]研究的Riccati型函数与函数类F*. 为了进一步的理解,读者可参考文献[17-19]等.
1 预备引理
这一部分的引理将被应用于第2部分主要结论的证明中.
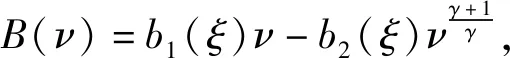
(1.1)
引理1.2 设(A1)-(A5)成立. 令x(ξ)是方程(*)的最终正解,则存在足够大的常数ξ1≥ξ0,当ξ≥ξ1时,y(ξ)必为如下二者情况之一:
(1)y(ξ)>0,y′(ξ)>0,(α1(ξ)(y′(ξ))γ)′>0;
(2)y(ξ)>0,y′(ξ)<0,(α1(ξ)(y′(ξ))γ)′>0.

由方程(*),(A3)和(A5),有
(α2(ξ)(α1(ξ)(y′(ξ))γ)′)′+α3(ξ)(α1(ξ)(y′(ξ))γ)′=
(1.2)
z(ξ)((α2(ξ)(α1(ξ)(y′(ξ))γ)′)′+α3(ξ)(α1(ξ)(y′(ξ))γ)′)=
(z(ξ)α2(ξ)(α1(ξ)(y′(ξ))γ)′)′<0,
(1.3)
这意味着z(ξ)α2(ξ)(α1(ξ)(y′(ξ))γ)′是递减的且最终定号. 又因为z(ξ)>0和α2(ξ)>0,所以有(α1(ξ)(y′(ξ))γ)′>0 或(α1(ξ)(y′(ξ))γ)′<0成立. 我们断言(α1(ξ)(y′(ξ))γ)′>0成立. 否则,(α1(ξ)(y′(ξ))γ)′<0. 由(1.3)式,存在ξ2>ξ1,当ξ>ξ2时,对正的常数M1,使得
z(ξ)α2(ξ)(α1(ξ)(y′(ξ))γ)′ (1.4) 成立. 对(1.4)式从ξ2到ξ积分得 (1.5) 利用(A1),若取ξ→∞,则α1(ξ)(y′(ξ))γ<0,这说明y′(ξ)<0成立. 又因为(α1(ξ)(y′(ξ))γ)′<0,所以存在ξ3>ξ2,当ξ>ξ3时,对于正的常数M2,有 α1(ξ)(y′(ξ))γ<α1(ξ3)(y′(ξ3))γ=:-M2 (1.6) 成立. 再次对(1.6)式从ξ3到ξ做积分,可得 由(A1),若取ξ→∞,则y(ξ)<0,这与y(ξ)>x(ξ)>0矛盾. 因此,(α1(ξ)(y′(ξ))γ)′>0. 下面证明y′(ξ)最终定号. 因为(α1(ξ)(y′(ξ))γ)′>0,所以α1(ξ)(y′(ξ))γ是递增和最终定号的. 利用α1(ξ)>0和γ是正奇数之比,得y′(ξ)最终定号. 因此,易得y(ξ)是满足情况(1)或(2)的. 证毕. (1.7) (z(ξ)α2(ξ)(α1(ξ)(y′(ξ))γ)′)′=z(ξ)((α2(ξ)(α1(ξ)(y′(ξ))γ)′)′+ (1.8) 对(1.8)式自ξ到∞积分,由m (1.9) 对(1.9)式自ξ到∞积分可得 (1.10) 在这一部分中,我们将建立方程(*)的新振动判据,为了简便,引入以下标记 定理2.1 设(A1)-(A5)和(1.7)成立. 若对任给l≥ξ0,存在δ(h)∈C1([ξ0,∞),+)和ρ(ξ)∈C1([ξ0,∞),+),在满足和时,使得 (2.1) 若y(ξ)满足(1),则 (2.2) 联立(*)与(2.2),得 (2.3) 又y(ξ)满足(1),故y′(ξ)>0且(α1(ξ)(y′(ξ))γ)′>0. 由(2.3),易得(α2(ξ)(α1(ξ)(y′(ξ))γ)′)′<0,且 (2.4) 也就是说, (2.5) 又因为g(ξ,s)≤ξ,所以 (2.6) 下面,对h≥ξ1时,定义广义Riccati型函数 (2.7) 显然,w(h)>0. 对w(h)微分得 由(2.3),(2.4),(2.6)和(2.7)计算知 (2.8) 对不等式(2.8)两边同乘函数δ2(h)(ξ-h)2α(h-l)2β,再从l到ξ积分得 (2.9) 且由分部积分计算可知 利用上述等式和不等式(2.9)得 (2.10) 因此, (2.11) 对该不等式取上极限得 该不等式与(2.1)矛盾. 若y(ξ)满足(2),由引理1.3,方程(*)的解趋于0. (2.12) 则对下面方程的所有解或者是振动的或者趋于0. (2.13) 证明首先,计算一个特殊积分 (2.14) (2.15) 利用(2.12)和(2.15),由于G(h)>0和ρ(h)>0成立,有 (2.16) 上述不等式满足定理2.1,也就是说,(2.13)式是振动或趋于0的. 证毕. (2.17) 则(2.13)式的解振动或趋于0. 选择γ=β=1,δ(h)=1,ρ(h)=G(h),有下面的推论. (2.18) 则(2.13)式的解振动或趋于0的. 证明方法与推论2.1类似,(2.14)仍成立,并额外给出以下几个特殊积分 于是 (2.19) 接下来,注意到G(h)中γ=1,计算知 (2.20) (2.21) 由(2.18)和(2.21),易得 因此,在β=1时,由定理2.1有(2.13)的解是振动或趋于0的. 证毕. 选择γ=α=1,δ(h)=1,ρ(h)=G(h). 则(2.13)的解是振动或趋于0的. 下面,对(2.7)式中Riccati型函数选择特殊的ρ(ξ),可以得到比之前更简洁的新定理. 定理2.2 设(A1)-(A5)和(1.7)成立. 对任给l≥ξ0,存在δ(h)∈C1([ξ0,∞),+)及足够大常数ξ1>ξ0,当满足和h>ξ1时,使得 (2.22)

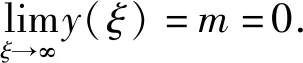

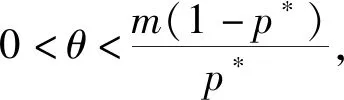

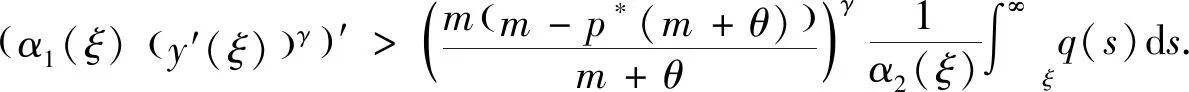
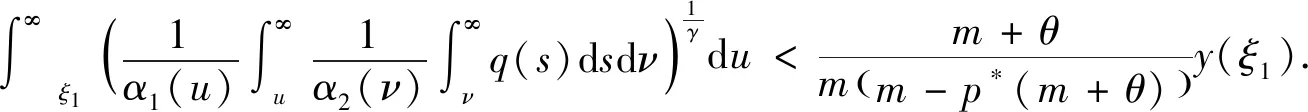
2 主要结论