基于非平稳时间序列的VAR模型实证分析*
刘玉娇, 吕玉华
(曲阜师范大学数学科学学院,273165,山东省曲阜市)
0 引 言
向量自回归模型(Vector Autoregression Model)早在1980年时就由Christopher引入到计量经济学中,由Christopher等对使用单个变量的自回归模型(AR模型)作出改进,提出可以使用多变量的向量自回归模型的观点.与在经济背景下建立模型的情况不同,VAR模型以数据统计性质为基础,把研究的经济系统中的每一个变量依次作为所有变量的滞后变量的函数来构造模型的.Dong等通过研究发现非平稳时间序列建模过程存在不规范问题.Jaime在对时间序列进行协整检验时发现AR模型不能很好地解决问题.张卫平提出在模型中引入两个变量作为额外信息,并基于VAR模型对通货膨胀进行预测,得到的绝大部分向量自回归模型均优于单变量的AR模型.Jean等提出建立VAR模型对变量的长期和短期关系的因果性做出判断和预测,自此VAR模型已经得到较为广泛的应用.王光栋,叶仁荪基于协整检验和VAR模型的建立对资本的投入与就业增长的关系进行实证分析对变量的短期和长期影响关系做出判断.Duo[10]从根本上解释了向量自回归模型本质,增强了它在计量经济学中的重要意义.董梅通过建立VAR模型分析出市场上各因素对居民消费价格指数的影响,并利用脉冲响应得出了CPI对自身反应较为敏感的重要结论.陈雨童等考虑在多变量情况下建立相关的VAR预测模型,对外汇储备的规模进行预测.郑桂玲等[11]引入向量误差修正模型(VEC)充分解释了居民收入对旅游消费的动态影响.章亚芬借助居民消费价格指数和货币供给量作为主要的宏观经济因素来分析它们与股票价格指数的影响关系,建模过程完整分析全面,但仅考虑了股票市场而忽略金融市场的其他部分可能会使所得结果较为片面.基于上述相关文献做出的研究,本文将采用向量自回归模型做实证分析.
针对近年来结构性就业矛盾、资本恶性循环带来的持续产能过剩和消费不足问题的出现,未来中国的经济能否继续保持快速的增长受到高度关注.依据中国1952—2008年的经济数据,根据协整理论和向量自回归的方法,对中国资本形成总额、从业人员人数与国内生产总值的因果性进行实证分析,并使用ECM模型变量之间的关系修正和评价.本文不仅采用多变量进行实证分析,利用协整检验建立VAR模型,同时还利用误差修正模型(VEC)对变量间的短期关系进行修正,对变量之间的关系预测有重要的意义.
1 VAR模型的建立
1.1 时间序列平稳化
1.1.1 非平稳时间序列的预处理
综合考虑数据可行性和国内经济金融现状等问题,本文采用的指标为1952—2008年国内生产总值(GDP),从业人员(E)及国内资本形成总额(GCF)的时间序列数据.由于这3个变量的时间序列有明显的趋势性,为非平稳时间序列,所以将变量取对数,得到数据的对数序列走势如图1所示,该图显示,时间序列经过对数变换后有截距项和趋势项,虽然趋势性有所减弱,但仍为非平稳序列.

图1 国民生产总值、从业人员、资本形成总额对数序列走势图
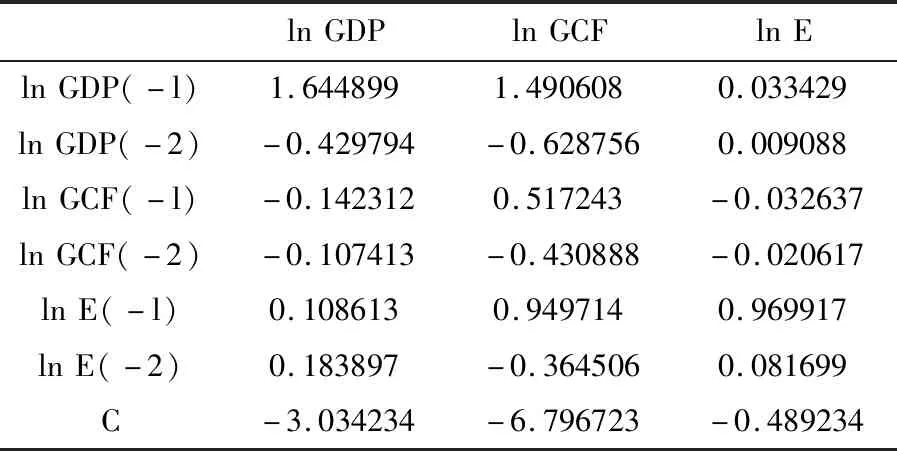
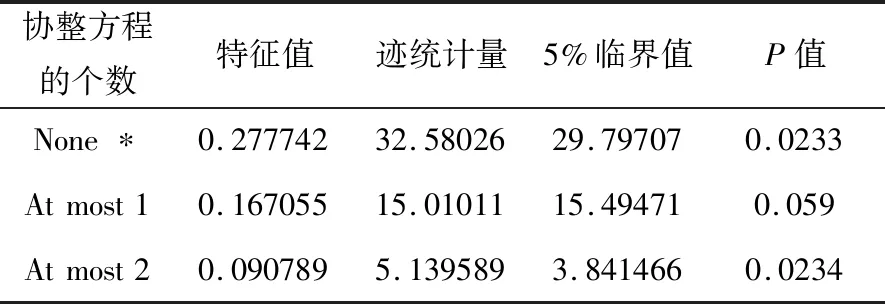
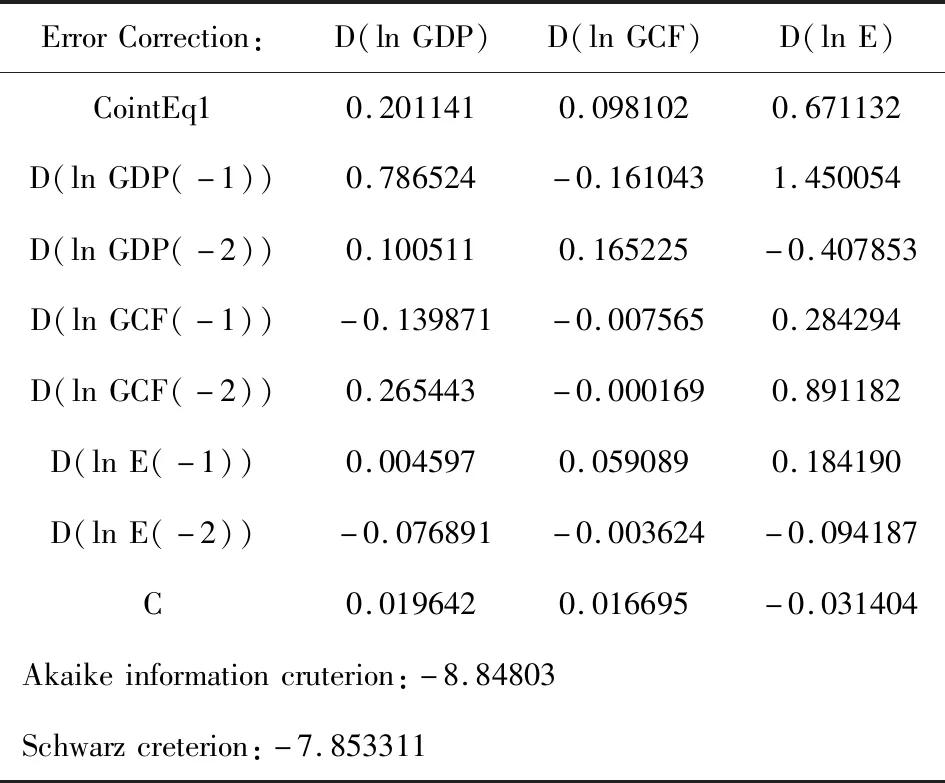
做ln GDP关于ln E和ln GCF的最小二乘回归,回归结果表明,R2的值为0.994366接近1,回归方程的拟合优度较高,但DW(Durbin-Watson)统计量值偏低,小于R2,根据Granger和Newbold经验性规则:当DW 1.1.2 ADF单位根检验 为了验证误差项是否存在自相关,采用ADF单位根检验方法.如果序列不平稳,则对序列进行一阶差分后再检验序列平稳性.给定原假设:时间序列存在单位根.平稳性检验的结果如表1所示. 表1 各变量的平稳性检验结果 表1中观察到ln GDP、ln E、ln GCF的ADF检验t统计量值均大于1%、5%和10%水平下的临界值,故不拒绝原假设,ln GDP、ln E、ln GCF都存在单位根,时间序列都是不平稳的.对变量进行一阶差分,3个变量时间序列的ADF统计量t值均小于临界值,故拒绝原假设,表明一阶差分后3个变量的时间序列不存在单位根,故这3个变量序列是一阶单整时间序列. 时间序列全部是一阶单整时间序列,如果变量间存在格兰杰因果关系,则符合建立模型的基本条件.首先进行格兰杰因果检验(Granger因果检验). 格兰杰因果检验也被称为外生性的Wald检验,事先假设有关变量y和x的预测信息全部包含在变量序列中,格兰杰因果检验对应的回归方程 (1) (2) 其中假设白噪声σ1t,σ2t不相关.给出两个方程的零假设 H00:β1=β2=…=βq=0; H01:δ1=δ2=…=δm=0. 通过方程可能得出如下结论: (1)x是y的单向因果原因.如果式(1)中的滞后项x的系数βj的估计显著不为0,式(2)中滞后项y的系数δj的估计显著为0,则称x是导致y变化的原因. (2)y是x的单向因果原因.如果式(2)中滞后项y的系数δj的估计显著不为0,式(1)中的滞后项x的系数βj的估计显著为0,则称y是导致x变化的原因. (3)当x和y的滞后项系数都显著为0时,两者无因果关系. (4)当x和y的滞后项系数都显著不为0时,两者互为因果关系. 将本文给出的3个变量分别作为内生变量进行Granger因果检验,结果如表2所示. 表2 Granger滞后2阶检验结果 对变量从业人员(E)、国内生产总值(GDP)和国内资本形成总额(GCF)的数据分析结果显示,在5%的显著性水平下,F值超过临界值Fα或P值小于0.05则拒绝原假设表明变量间存在格兰杰因果关系.结果显示E是GCF的格兰杰原因,GDP是GCF的格兰杰原因,GCF是GDP的格兰杰原因,即两者具有双向的格兰杰因果关系.即从业人员数量会对资本形成总额造成显著影响,同时也观察到资本形成总额与国内生产总值相互间的影响显著. 1.3.1 建立模型 根据时间序列变量建立VAR模型从而判断变量之间的相互关系.首先需要判断模型的最小滞后期.结果如表3所示,表的第1列表示各个指标的选择的滞后阶数,给出滞后长度判断准则统计量 LR、FPE、AIC、SC和HQ,带*最多的就可以确定是最小滞后期的一行,判断出该模型滞后2阶,与原模型的估计是相符的,故可以写出VAR模型.具体结果见表4. 表3 最小滞后长度的选择 表4给出了模型的参数估计,表的每一列代表VAR模型中每一内生变量的方程,对应数值为待估系数,得到VAR模型的估计为 表4 VAR模型估计 1.3.2 VAR模型的稳定性检验 得到模型的估计式后需要对模型的有效性进行检验.首先检验残差是否服从正态分布,表5结果显示在1%显著性水平下的J-B统计量检验值大于临界值,P值大于0.01,不拒绝原假设,即残差服从正态分布. 表5 残差正态分布检验 对向量自回归模型做滞后期为2的VAR(2)的多项式逆根检验,如表6所示,结果表明根的模长全部小于1,对应的单位根全部落在单位圆中,该VAR模型通过了逆根检验. 表6 逆根检验表 经过检验可知该滞后二阶的向量自回归模型的残差序列服从正态分布,且全部单位根都在单位圆里,故而有足够的理由认为VAR模型的建立基本正确,认为该模型具有稳定性. 1.3.3 Johansen协整检验 本文所研究的变量关系为多变量关系,所以需要采用多变量协整关系的检验方法—极大似然法检验,也称为Johansen协整检验.协整具有十分重要的经济意义,尤其是在包含多个变量的复杂模型中,每个变量都有其各自的长期波动规律,若存在协整关系,则证明这些变量之间存在一个长期稳定的均衡关系. 给出假设: H0:有0个协整关系; H1:有r个协整关系. 协整检验结果如表7显示,原假设None代表原假设为“至多有0个协整关系”,在5%的显著性水平下,迹统计量32.58026大于临界值29.79707,P值小于0.05,不接受原假设,认为存在协整关系;当原假设为“最多存在一个协整关系”时,在5%的显著性水平下,迹统计量15.01011小于临界值29.79707,P值大于0.05,接受原假设,认为最多存在一个协整关系,检验结束.通过该协整检验可判断出该模型存在一个协整关系,变量之间存在长期均衡关系. 表7 协整检验 在解决实际问题时,为观察整个VAR模型在被某一扰动项冲击时造成的全部影响,需要用脉冲响应函数来分析扰动项的影响是如何传送到各个变量的. 首先给出引入滞后算子形式的VAR模型 B(L)yt=εt,t=1,2,…,T, 其中B(L)=Ik-B1L-B2L2-…-BnLn是滞后算子多项式. 由于VAR(n)是可逆的,故有 yt=D(L)εt, 其中D(L)=B(L)-1=D0+D1L+D2L2+…,且D0=Ik(k阶单位阵). 第i个方程为 (3) 采用脉冲响应函数进行脉冲研究,最终得到如下脉冲响应函数图2. 图2 脉冲响应函数图 3个脉冲响应函数图各自代表ln GDP、ln E、ln GCF在分别受到ln GDP、ln E、ln GCF的扰动项冲击时的变化趋势.以国内生产总值ln GDP的脉冲响应函数为例,从第1期开始ln GDP对自身的标准差信息有较强的反应,国内生产总值增加约0.06,到第2期反应增强为0.08;ln GCF对ln GDP的影响第1期为零,从第2期开始有一个负向的影响并逐渐增强;ln E对ln GDP的影响几乎为零.通过观察可以发现一个变量往往会对其自身的标准差信息立刻产生较强的反应. 方差分解是把向量自回归模型中的一个变量的方差分解到系统的各个扰动项上去,通过显示每个扰动项对各变量影响的相对程度来把握各个变量之间的影响关系.方差分解的基本思想是:由式(3)可知,右边括号内是第j扰动项uj从过去无限远至现在时点对第i内生变量yi影响的总和.在E(εj)=0,εj无序列相关的假设下,对其求方差,可得 它是把第j个扰动项从过去无限远至现在时点对第i个内生变量yi影响的总和,利用方差加以评价的结果. 令Cov(εt)=E(εtεt′)=Σ,则yit的方差为 t=1,2,…,T. 其中RVCj→i(∞)表示到达无限远时间的第j个变量在扰动项冲击下的方差对y的方差贡献率.各变量方差贡献率如表8所示. 表8 方差分解 由方差分解图可知,ln GDP对其自身的贡献率,达到100%,到第10期下降到53.92%,ln E和ln GCF对ln GDP的贡献率呈上升趋势,到第10期为止由0分别增加到11.71%和34.37%;ln E的自身方差贡献率极大且较稳定,约占自身信息的90%,ln GDP和ln GCF对其贡献率较小且呈现稳定状态;ln GDP和ln GCF对其方差贡献率较小,几乎可以忽略不计.ln GCF对其自身的方差贡献率第1期为45.07%,而ln GDP对ln GCF的贡献率为54.93%,比它本身的贡献率还要大,这与之前的Granger检验的分析结果相一致,ln E对ln GCF的贡献率第1期为0,后期有小幅度上升趋势. 通过对非平稳时间序列的协整性检验,基本确定了变量之间的长期均衡关系.要想建立短期动态模型,需要在协整关系确定的基础上构建误差修正项从而调整VAR模型以增强短期关系的稳定性,该调整过程即误差修正模型的建立过程.该模型的目的在于提高VAR模型的精度,弥补长期静态模型的不足. VAR模型可以写为 yt=A1yt-1+A2yt-2+…Apyt-p+εt,t=1,2,…,T. 将该式进行协整变化可得 (4) 如果yt存在协整关系,则式(4)可写为 误差修正结果如表9所示: 表9 VEC参数估计检验 表9给出误差修正模型的参数估计结果和检验结果.参数含义与前述VAR模型相似,其中,AIC统计量和SC统计量代表模型的拟合程度,统计量的数值越小拟合程度越好.AIC=-8.847803,SC=-7.853311,数值较小说明该模型拟合效果较好,VEC模型较为稳定. 本文针对非平稳时间序列建立向量自回归模型,通过Granger因果检验法,研究了我国国内生产总值,从业人员数量和资本形成总额之间的相互关系.检验发现从业人员数量是资本形成总额的格兰杰原因,资本形成总额与国内生产总值之间互为格兰杰因果关系.再进一步通过Johanson协整检验,脉冲响应和方差分解法,并利用误差修正模型得出结论:(1)GDP与从业人员数量和资本形成总额之间存在存在协整关系,从长期均衡角度来看,他们之间的作用会逐渐趋于稳定;(2)从业人员数量对GDP有促进作用,GDP对资本形成总额的增长有促进作用,而资本形成总额对GDP有反向作用不利于GDP的增长,与实际情况有所不同,故可能存在其他变量的干扰,有待进一步分析. GDP的增长能够反映经济发展现状良好,国民收入增加,消费能力的提高和进步,它反映了我国的经济实力和市场规模现状.因此提高人才市场活跃度,增强我国综合国力对实现中华民族伟大复兴具有重要的经济意义.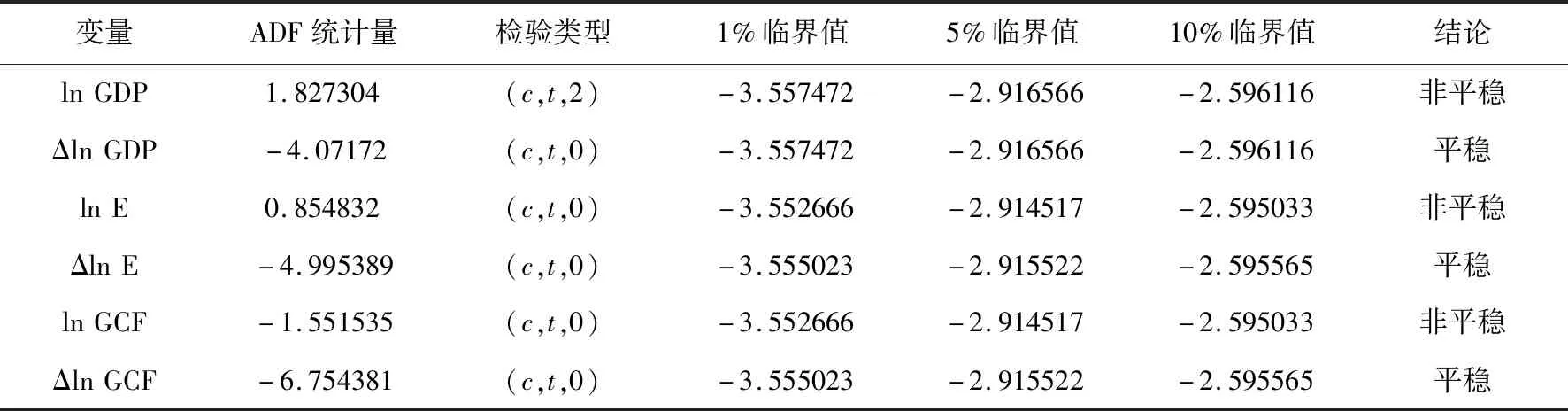
1.2 Granger因果检验


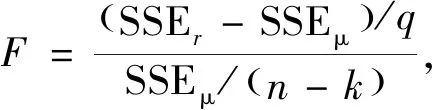

1.3 VAR模型的建立与Johansen协整检验




2 脉冲响应与方差分解
2.1 脉冲响应


2.2 方差分解


3 向量误差修正模型(VECM)


4 评价与总结

