巧用“类比” 活学“实数”

潘海波

从前，有个县遭了灾，村民们推荐一个老者去衙门报告灾情，请求减点税。老者来到县衙，县官问他：“小麦收了几成？”老者答：“五成。”“棉花呢？”“三成。”“玉米呢？”“两成。”县官听了大怒道：“有了十成收获，年景不坏，你还来报灾，真是大胆！”老者忙说：“我活了180岁，还没有遇到过如此严重的灾情啊！”县官听了说：“胡说！你怎么活了180岁呢？”老者说：“大儿子50岁，二儿子30岁，小儿子20岁，老汉我今年80岁，合起来正好180岁，一点儿也不胡说。”县官拍着桌子说：“哪有如此算法？”老者说：“大老爷息怒！刚才你计算收成，不也是这样算的吗？”

这则故事中，老者驳斥昏庸无道的县官，用的就是类比的方法。在实际生活中，我们把一些“似曾相识”的事物加以比较，常常会有新的发现。在数学学习中，“把类似问题进行比较和联想，由一个数学对象已知的性质迁移到另一个数学对象上去，从而获得另一个数学对象的性质”，这种思维方法就是类比。

实数的知识点与之前许多知识点有很多类似之处，下面我们将采用类比的方法加以学习。

一、概念类比

1.平方根与立方根。

从平方根与立方根的概念上看，两者的表述方式完全一样：如果一个数的平方等于a，那么这个数叫作a的平方根，也叫二次方根，求一个数的平方根的运算叫作开平方，开平方与平方互为逆运算;如果一个数的立方等于a，那么这个数叫作a的立方根，也叫三次方根，求一个数的立方根的运算叫作开立方，开立方与立方互为逆运算。

从方根的个数上看，只有非负数才有平方根，正数有两个平方根，它们互为相反数，0的平方根是0，负数没有平方根;任何一个数都有立方根，正数的立方根是正数，0的立方根是0，负数的立方根是负数。

从符号表示上看，一个数a的平方根，记作±[a];一个数a的立方根，记作[a3]。

2.有理数与实数的其他概念。

我们知道：一个正有理数的绝对值是它本身，一个负有理数的绝对值是它的相反数，0的绝对值是0。类似地：一个正实数的绝对值是它本身，一个负实数的绝对值是它的相反数，0的绝对值是0。事实上，无论是在有理数范围内，还是在实数范围内，相反数、倒数的意义及求法都是一样的。

另外，有理数与实数在数轴上的点的对应关系也是类似的。任何一个有理数都可以用数轴上的点来表示，任何一个实数也都可以用数轴上的点来表示;反过来，我们要注意，数轴上的点都可以表示一个实数，这里既包括有理数，又包括无理数，而不仅仅只表示一个有理数。

二、分类类比

有理数，将其按性质可以分为整数和分数（如图1），按符号可以分为正有理数、0和负有理数（如图2）。

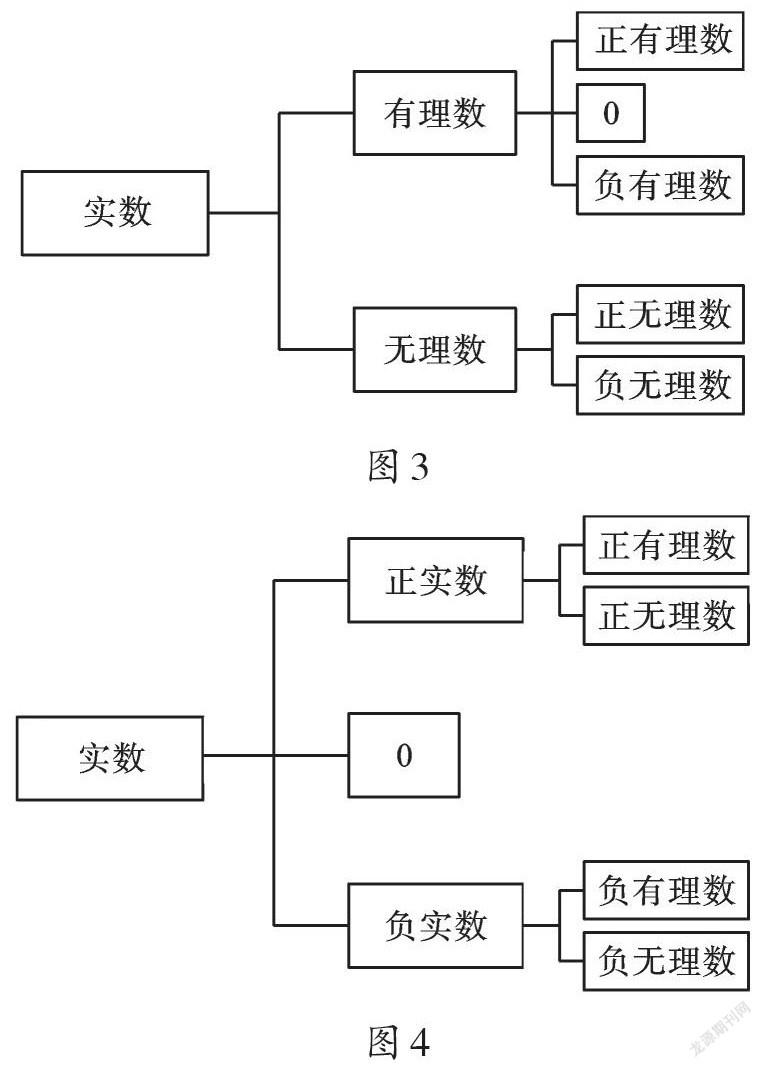
类似地，实数按性质可以分为有理数和无理数（如图3），按符号可以分为正实数、0和负实数（如图4）。

三、运算类比

在有理数范围内，运算法则包括加、减、乘、除、乘方。运算顺序为：先算乘方，再算乘除，最后算加减，如果有括号，就先算括号里的。运算律有加法交换律、加法结合律、乘法交换律、乘法结合律、乘法分配律。同样，在实数范围内，这些运算法则、运算顺序、运算律仍然适用。

著名數学家波利亚说过：“类比是一个伟大的引路人。”希望同学们在以后的学习中不断领会，并加强运用。

（作者单位：江苏省常州市实验初级中学天宁分校）