人工噪声辅助可见光通信保密速率最大化研究

施 歌,李 勇,程 伟

(西北工业大学 电子信息学院, 陕西 西安 710129)

0 引言

可见光通信(visible light communication, VLC)结合了通信和照明技术，在过去十年中受到越来越多研究者的关注。与传统的射频(radio frequency, RF)技术相比，它具有实施成本低和频谱源丰富等优势[1-3]。尽管前景广阔，但由于其广播特性，VLC系统实际的部署仍然面临安全问题的挑战。最近，物理层安全(physical layer security, PLS)已经成为一种有前途的技术，可以保护无线通信并补充传统应用层[4-6]上的加密技术。在射频(radio frequency, RF)网络中，近几十年来，研究人员已经对RF系统中的物理层安全问题进行了深入研讨[7-10]。但是，与RF系统相比，VLC系统具有一些不同的特性。例如，VLC通道调制信号是实数且为正值。由于发光二极管(light emitting diode,LED)的线性动态范围有限，VLC系统的信号输入受到峰值幅度约束的限制。因此，在VLC系统中，PLS的一些优化问题值得被重新审视。

多输入单输出(multiple input single output, MISO)和多输入多输出(multiple input multiple output, MIMO)是利用空间复用增益来增强VLC系统安全性能[11-15]。在室内使用多个LED阵列并且形成MISO传输是很自然的，因为它可以保证房间内照明充分且均匀。文献[11]利用波束成形的方法，求解多输入单输出多窃听者(multiple input single output multiple eavesdroppers, MISOME)信道的可达保密速率，并且仿真结果表明：迫零(zero-forcing, ZF)是近乎最优的安全传输策略。文献[14]提出了一种预编码方案，旨在增强最大化受峰值幅度约束的多用户MISO VLC广播信道的保密性能，数值结果表明：该方案优于常规的ZF预编码。文献[15]在采用同步光信号和功率传输技术的MISO VLC网络中，考虑了保密波束成形设计，在理想信道状态信息(channel statement information, CSI)和有界误差CSI模型下最大化保密速率。除了使用波束成形来削弱窃听者的接收效果外，提高物理层安全性能的另一个方法是人工噪声[11-12](artificial noise，AN)。文献[11]设计了一个多LED干扰器，向VLC系统中的窃听者发射虚假干扰信号，并且不会干扰合法用户。文献[12]设计了一种最佳功率分配，在峰值幅度约束下增强广义空间移键控VLC系统的保密性能。然而，在MISO VLC系统保密性能最坏的情况下，即多个配备有多个光敏二极管(photodiode，PD)窃听者的情况下，保密信号和干扰信号协方差之间的最优功率分配，目前没有文献研究。

本文探讨在配备多PD窃听者的MISOME VLC信道中，人工噪声辅助保密速率最大化(secrecy rate maximization, SRM)问题。在该问题中，考虑对保密信息协方差和AN协方差进行联合功率优化。该问题的主要困难在于AN协方差使得目标函数不凸且难以优化。为了解决这个问题，通过推导得出了SRM问题的等效问题，转换后的等效问题变成了凸问题且更容易解决。SRM问题被重塑为基于单变量半正定规划(semidefinite programming, SDP)问题，并且可以使用凸优化工具箱(convex optimization toolbox, CVX)轻松求解。在SRM问题中，假定保密信息和AN都具有通用的发射协方差，即没有将发送策略固定为波束成形或将AN限制在合法信道的零空间中。在推导等效SRM问题时，本文证明了发送波束成形是机密信息传输的最佳策略。该结果对于在VLC场景中使用波束成形提供了有意义的理论依据。

1 系统建模

本文设计一个室内VLC系统，该系统具有M个LED阵列和一个配备有单个PD的合法用户。合法用户的信道会被K个窃听者偷听，并且每个窃听者都配备有Lk个 PD。所有的LED阵列都连接到一个中央控制单元(central control unit,CCU)，以便收集有关合法用户和窃听者的位置和通道增益信息，并且CSI可以通过RF或其他介质作为上行链路传输提供给CCU。在文献[16-18]中，此假设已被广泛用作合理模型。在CCU中，中央处理器会设计发射协方差矩阵并分配给LED阵列。s∈M作为LED阵列发送的信号矢量，合法用户和第k个窃听者接收到的信号分别表示为：

(1)

其中：k∈κ≜{1,2,…,K}；h={h1,hm, …,hM}T∈M，为从LED阵列到合法接收者的信道增益响应矢量；Gk={g1,glk, …,gLk}∈M×Lk是从LED阵列到第k个窃听者的通道增益响应矩阵；噪声nb和ne,k是独立的均匀分布的圆对称高斯噪声，其方差为N(0,δb2)和N(0,δe,k2I)。由于直射信道(line of sight, LoS)分量的信号强度远高于非直射信道分量[18]，因此本文仅考虑LoS的分量。从第m个LED阵列到合法用户的直射信道增益[19]可以表示为：

(2)

其中：β为朗伯照射次序；Ar为接收者PD的接收面积，m2；dm为从第m个LED阵列到合法用户的距离，m；φm为第m个LED阵列的发射角，(°)；φm为合法用户接收器PD的入射角，(°)；gof为光学滤波器的增益；f(φm)为光学聚光器的增益[14]。从LED阵列到窃听者的信道建模类似于式(2)，主要取决于系统参数和它们的相对位置。本文采用了一种基于AN的方案，以降低窃听者的接收效率。发送信号是保密信息和AN的和，即s=x+z。假定保密信号矢量x遵循高斯分布x～N(0,W)，其中，W是保密信息的协方差矩阵。对于AN，本文假设z～N(0,Σ)，其中，Σ为AN协方差矩阵。保密信号向量和AN信号向量都是统计独立的随机变量。在本文中，为实现最大保密速率，需要设计保密信息协方差和AN协方差。给定(W,Σ)，可达保密速率表示为[8]：

(3)

其中：Rb(W,Σ)为合法用户的可达速率；Re,k(W,Σ)为第k个窃听者的可达速率。该系统的安全性能是通过选取所有K个窃听链接中的最小保密速率获得的。合法用户和窃听者的可达速率的公式如下：

(4)

可达保密速率Rs能实现完美保密，即合法用户能以Rs的速率正确地解码机密信息，而窃听者不能解码任何信息。根据VLC的光学特性，本文考虑峰值幅度受约束的信号输入，以确保人眼安全和光学设备的正确使用。发射信号s的峰值幅度限制条件如下所示[20]：

‖s‖∞≤A,

(5)

其中：‖·‖∞为向量的无穷范数；A为光信号的振幅允许最大数值，A≥0。在文献[21]中，上述约束被松弛为E(|sisj|) ≤A2, 1≤i,j≤M。通过该方法，可将协方差矩阵的功率峰值幅度约束写为：

‖W+Σ‖max≤A2,

(6)

其中：‖·‖max为最大范数，限制矩阵中元素的最大绝对值。为了在总功率约束和功率峰值幅度约束下获得输入协方差矩阵的最优设计，本文提出了一个求最大保密速率的问题，如下所示：

maxRss.t. Tr(W+Σ) ≤Pt, ‖W+Σ‖max≤A2,W≥0,Σ≥0,

(7)

其中：Pt≥0是LED阵列的总功率预算。在这个问题中，除了目标函数以外，所有的约束条件都是凸的。因此，需要采用一种方法来解决该目标函数的非凸问题。

2 基于SDP的问题解决方法

本文提出了一种基于半正定规划的优化方法，以数值的方式解决SRM问题。首先，使用松弛变量β重写问题：

(8)

其中：logβ可以解释为窃听链路的可达速率。此步骤为等效变换，可以通过调整β的值找出最佳解决方案。在此问题中，具有挑战性的部分位于式(8)的非凸目标函数和第1个非凸约束条件中。为了克服这个困难，本文将首先通过使用夏恩-库珀变换来重写分数形式的目标函数，然后利用一个不等式来简化式(8)的第1个非凸约束条件。首先，做出以下定义：

(9)

问题(8)重写如下：

(10)

直观上来说，该想法是约束分母为一个与β相关的定值，让分子成为目标函数。将ξ>0替换为ξ≥0不会失去最优性，可以通过对问题(10)的任何可行解都不能为零的矛盾进行验证。但是，由于式(10)中的第2个约束条件非凸，该问题仍然没有变成凸问题。因此，需要介绍文献[8]中的一个引理，如下所示：

(11)

已知问题(19)是凸的(因为目标函数是仿射的，并且约束条件是仿射且正半定的)，因此斯莱特(Slater)条件成立，KKT条件足以实现最优性[22]。下式求出了该问题的拉格朗日(Lagrange)公式：

(12)

其中：νij,φ≥0是功率峰值幅度约束和总功率约束的拉格朗日乘数。M1,M2≥0是两个半正定协方差矩阵的拉格朗日乘数。Qk≥0,φ≥0分别是式(10)中第2行针对第k个窃听者的信干比约束和第1行等式约束的拉格朗日乘子。根据一阶条件得到：

(13)

(14)

对于等式的右侧，除了V外，其他项为半正定。即使矩阵V内所有元素大于零(vij≥0)，也不能确定它是半正定。因此，为了继续推导，本文提出了一个简单的引理，如下所示：

(15)

(16)

根据数学统计的知识，两个随机变量a和b之间的相关性[24]表示为：

(17)

这意味着协方差的绝对值小于或等于两个变量中的最大的方差值。因此，假设Var(a)≥Var(b)，有：

(18)

由此可知，两个随机变量中，至少一个变量的方差大于其协方差。协方差矩阵是由在对角线上的方差和协方差组成，这意味着可以始终在协方差矩阵的对角线位置上找到具有最大值的元素。因此，如果需要矩阵所有元素小于A2，那么只要对角线上元素小于A2即可，即引理2成立。通过使用引理1，最终将原始问题转换为凸问题，如下所示：

(19)

其中：β值表示为

1≤β≤1+min (Pt,MA2)‖h‖2,

(20)

其中：右侧的不等式基于瑞利商。目标函数对于某个β变为一个凸函数，而原问题变成一个基于β的半正定规划问题，并且可以通过CVX工具箱进行求解。通过在β取值范围上执行一维线性搜索，可以获得使目标函数最大的β*值，从而求出最大保密速率R*，使用如下公式：

(21)

对于一个特定的β值，问题(19)的复杂度取决于内点法的复杂度，而内点法的复杂度取决于变量和线性约束的数量。因此，在最坏的情况下求解一个SDP问题的复杂度是Ο(((2+K+M)4)0.5)，其中，2+K+M是式(19)中的约束条件个数。

3 仿真结果

使用仿真结果来分析所提出的AN辅助方法在室内VLC系统中的安全性能。LED阵列均匀朝下悬挂在天花板上，合法用户和窃听者面朝上放置在同一高度。合法用户和窃听者的位置均在房间内随机生成。仿真参数见表1。

表1 仿真参数

在仿真中，本文将所提出的最优AN辅助方法分别与基于各向同性AN辅助方法和无AN辅助方法进行了比较。在基于各向同性AN辅助方法中，AN协方差的结构由下式给出[7]：

(22)

图1 保密速率与总功率的关系

图1为保密速率与总功率的关系。图1在绘制了两种情况下相对于总功率的保密速率，即一个窃听者(K=1)和多个窃听者(K=3)。在单窃听者情况下，AN辅助方法的性能与无AN辅助方法相同，这表明在只有一个窃听者的情况下，使用人工噪声对该系统的保密速率没有明显帮助。但是，对于多个窃听者(K=3)的情况，所提出的AN辅助方法的保密速率明显优于其他方案，并且随着总功率的增加，它们的性能差距会逐渐增大。图2为保密速率与窃听者数量的关系。由图2可知：随着窃听者数量的增加，所提出最优AN辅助方法和基于各向同性AN辅助方法的性能同时下降，这是因为更多的功率需要用于干扰窃听者的传输。无AN辅助方法的性能急剧下降，因为在没有任何人工噪声干扰的情况下，具有良好信道状态的窃听者可轻松窃听机密信息。此外，本文提出的AN辅助方法比其他方法具有更好的性能，并且随着窃听者数量的增加，性能首先趋于平稳。图3为保密速率与LED阵列数量的关系。由图3可知：安全性能随LED阵列数量的增加而增加，这是因为合法用户获得了更多的阵列增益以提高其自身的安全性能。当LED阵列数量增加，无AN辅助方法的保密速率提高并接近AN辅助方法的保密速率。这意味着如果有足够大的自由度(degree of freedom, DoF)，系统仅需要使用很少或不需要AN来改善安全性能。

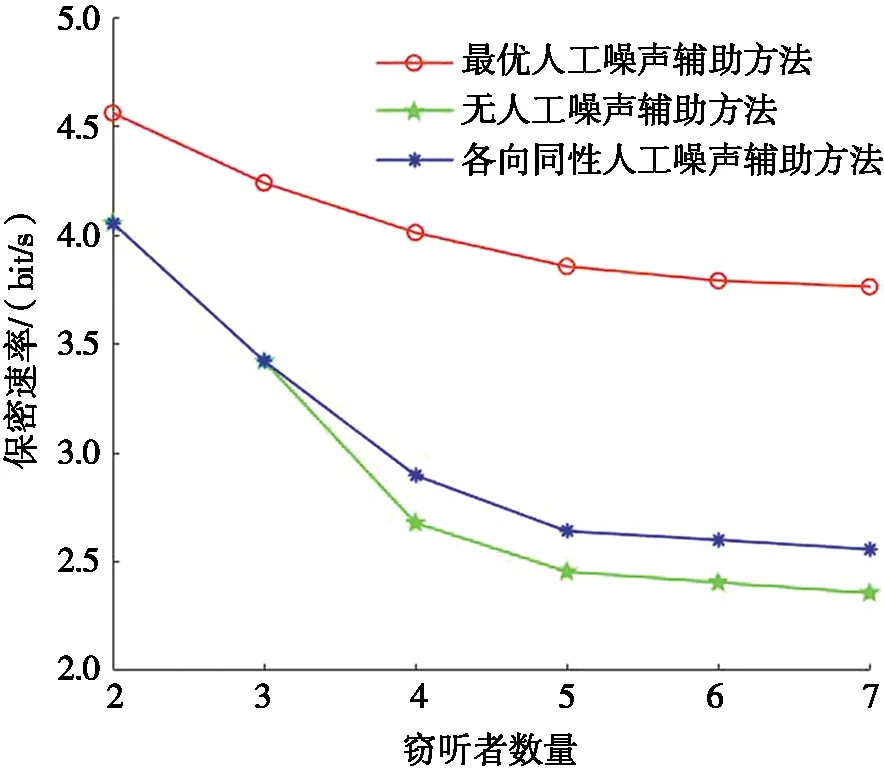
图2 保密速率与窃听者数量的关系

4 结论

本文针对保密速率最大化问题，在配备有多个光敏二极管的多窃听者的MISO-VLC系统中，设计了一种基于人工噪声的最优传输方法。为了求解保密信息协方差和噪声协方差的最佳功率分配方案，本文提出了一种将原始SRM问题转换为凸问题的方法，并使用一维搜索对该凸问题进行求解。通过推导该问题的KKT条件，证明了波束成形是保护保密信息的最佳方法。此外，某些参数会对安全性能产生巨大影响，例如，LED阵列的数量和总功率，而其他参数则以较小的方式影响安全性能。最后，有两种情况可能不需要AN来增强传输保密性，即只存在一个窃听者的VLC系统，或是该系统具有较多的LED阵列数量，且远超过窃听者的自由度。