基于模糊Kalman滤波的港口车辆组合定位方法研究
杨勇生,迟景成,姚海庆
(上海海事大学 物流科学与工程研究院,上海 201306)
0 引 言
港口环境下无人车辆的正常工作依赖于高精度的定位系统,磁钉、磁带导航是目前智能港口中应用较为广泛的定位方式,这些方法满足了智能港口环境下无人车辆对于定位精度的要求,但存在建设成本高、车辆行驶路径受限等问题.北斗卫星导航系统(BDS)/惯性导航系统(INS)组合定位系统是一种较成熟的定位方案,其定位精度高、建设成本相对低廉,能有效弥补磁钉、磁带导航中存在的车辆行驶路径受限等问题,是一种理想的智能港口无人车辆定位解决方案.
BDS/INS组合定位系统多采用Kalman滤波作为主要的滤波方式.港口环境下金属建筑物众多,易对BDS接收机信号造成遮挡,造成短时间内BDS定位精度的下降乃至失效,导致系统量测噪声的增大进而影响滤波效果,针对这一问题,通常采用自适应滤波技术对模型参数、噪声特性进行修正以改善滤波精度,模糊Kalman滤波是当前效果较为理想的方法之一[1].
利用模糊算法与Kalman滤波相结合的方式,将每一时刻的残差实测方差与实际方差的比值作为模糊控制器的输入,修正Kalman滤波中量测噪声协方差阵,以提高系统的定位精度与鲁棒性[2].
以加速度计采集值作为模糊控制器输入,自适应地估计Kalman滤波量测噪声方差.二者所提出的方法滤波结果较好,但实现过程较为繁琐.本文在将模糊控制器与Kalman滤波相结合的基础上,利用BDS传感器的工作状态作为输入,设计了一种易于实现的模糊逻辑控制器,利用该控制器对Kalman滤波中量测噪声方差进行实时调整,以提高在恶劣条件下系统的定位精度.通过港口环境下无人车辆的实验数据对该算法进行了验证,实验表明提出的算法相较于传统算法定位精度更高,且具有更好的鲁棒性.
1 模糊Kalman滤波
对于一般的连续系统,其离散化的状态方程与量测方程为[3]:
X(k)=Φk,k-1Xk-1+Γk,k-1Wk-1,
(1)
Zk=HkXk+Vk.
(2)
式中:Φk,k-1为k-1时刻到k时刻的状态转移矩阵;Hk为系统的量测矩阵;Γk,k-1、Wk,k-1、Vk分别为系统的噪声驱动矩阵、过程噪声、量测噪声[4].
对上述系统应用Kalman滤波基本方程可得扩展Kalman滤波(EKF)的递推方程:
预测方程:
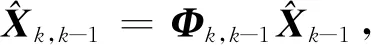
(3)
(4)
更新方程:
(5)

(6)
Pk=[I-KkHk]Pk,k-1.
(7)
式中将实际量测量与量测量的估计值的差值定义为预报残差,通称新息,即
rk=Zk-HkXk,k-1.
(8)
理想状态下新息均值为零.在这一状态下,常规Kalman滤波的量测噪声方差一直采用初始状态先验值,Kalman滤波器的结果较为理想.但是在现实条件下量测噪声具有显著的随机性,量测噪声保持不变将导致滤波结果精度的下降乃至滤波结果的发散[5].为了得到精确的滤波值,需要对系统的量测噪声方差进行实时的调整.
将式(5)改写为
tkRk]-1
(9)
式中,tk是通过模糊推理系统(FIS)得到的在k时刻对量测误差方差进行修正的数值[6].相较于传统Kalman滤波,模糊Kalman滤波通过不断地对量测方差进行调整,以得到更为精确的滤波结果.
在模糊Kalman滤波当中,FIS决定了滤波结果的质量.现阶段多以新息的实测方差与理论方差的比值作为FIS的输入来进行FIS的设计.下面将介绍一种基于传感器工作状态的模糊Kalman滤波.
2 基于传感器工作状态的模糊Kalman滤波
在BDS系统中,实时动态(RTK)载波相位差分技术的解算状态是影响定位精度的重要因素;在相同解算状态下,系统搜星数对定位的精度有着一定的影响;在车速固定的情况下,BDS位置与估算位置距离的大小也是衡量BDS信号好坏的一个标准.根据以上特点,采用多输入单输出的设计模式,将上述三个指标进行模糊化作为FIS的输入,输出值为t,设计了模糊逻辑控制器.用N表示BDS的搜星数,将其划分为四个模糊集,分别是Z、PS、PM、PB;根据RTK的四种解算状态将其划分为1、2、3、4四个模糊集,分别对应单点解、差分解、固定解与浮点解;根据GPS位置与估算位置差值d的大小,将其划分为PS、PM、PB三个模糊集.选取合适的隶属度函数对以上各个模糊集进行描述,得到的隶属度函数如图1、图2、图3所示:
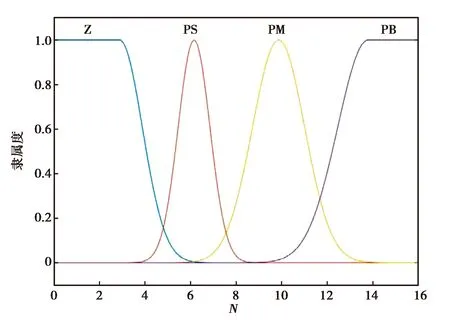
图1 搜星数N隶属度函数

图2 RTK解算状态隶属度函数

图3 IMU估计误差d隶属度函数
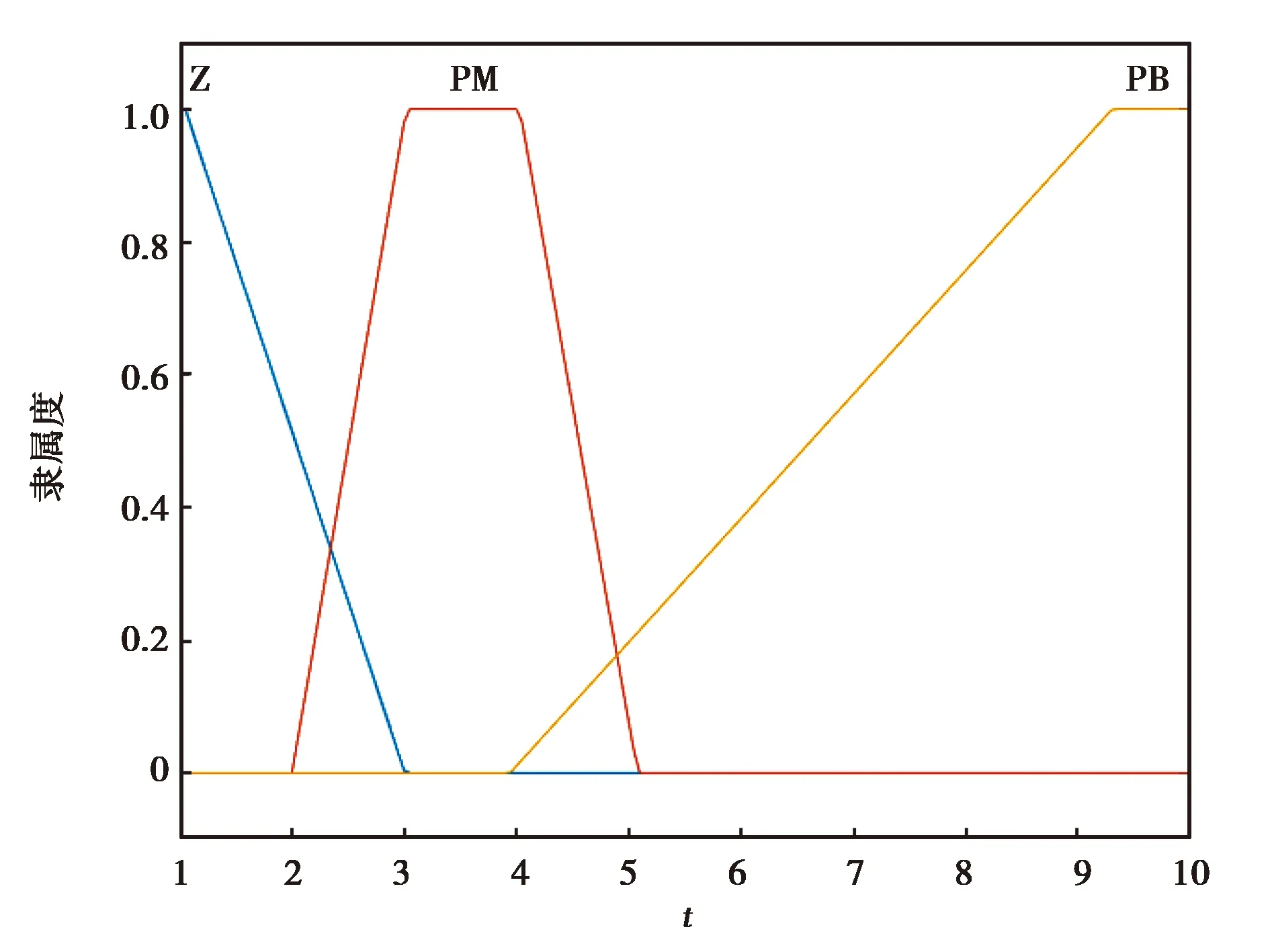
图4 量测误差调整参数t隶属度函数
模糊逻辑控制器的输出分为Z、PM、PB三个模糊集,其隶属度函数如图4所示.
根据经验,当BDS的解算状态为固定解的时候,定位精度最高,差分解、浮点解次之,单点解定位精度最差;在解算状态相同的条件下,BDS定位精度随搜星数的增加而提高;车辆匀速行驶的情况下,BDS估算位置与加速度计估算位置相差越大,BDS数据出现故障的几率越大.根据以上经验设计了模糊规则.同时考虑到模糊规则的数量对算法的运行速度的影响,通过忽略小概率事件的方式对模糊规则进行了简化(例如当搜星数小于等于4时解算状态为固定解的概率几乎为零,故在设计模糊规则的时候将这一组合忽略).经过试验与调整,得到模糊逻辑控制器的输出如图5所示:

图5 模糊逻辑控制器输出(RTK-d)
所采用的模糊卡尔曼滤波器的系统结构采用输出矫正的方式,结构图如图6所示:
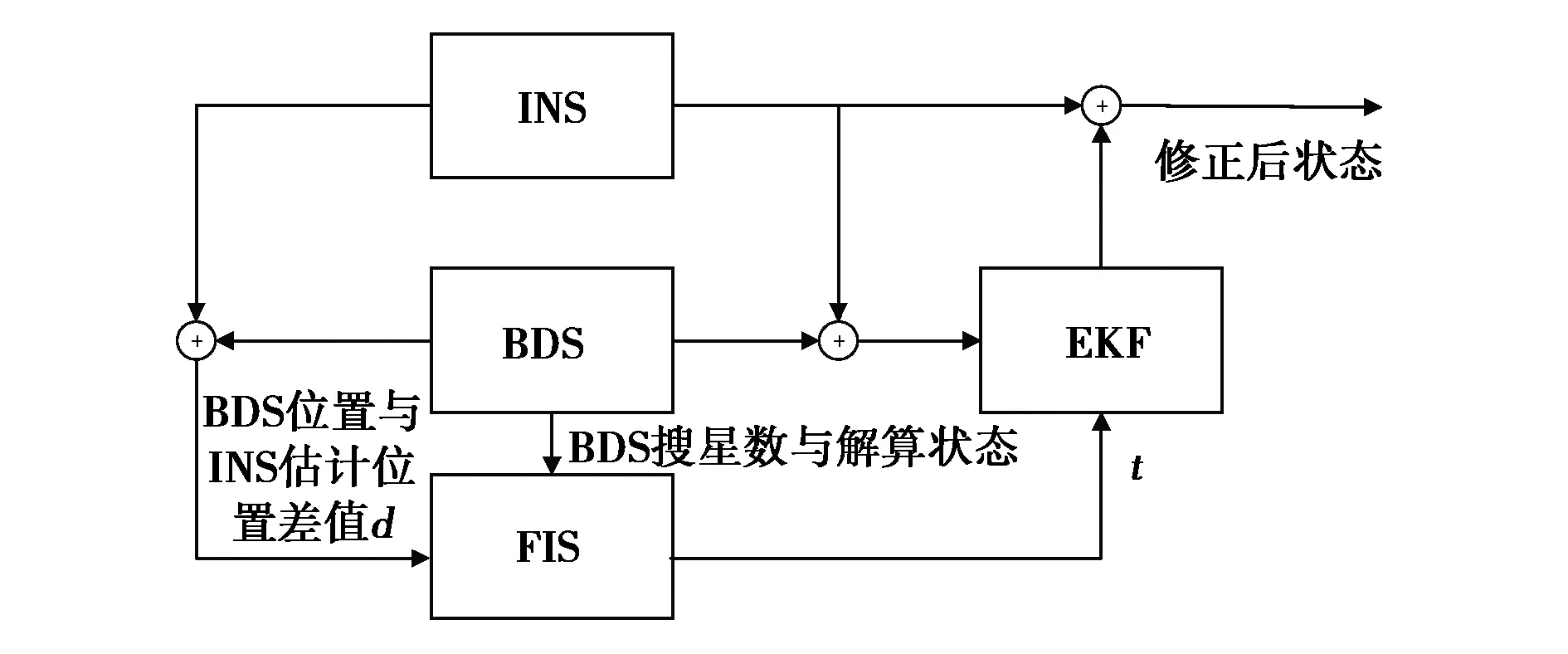
图6 模糊Kalman滤波器系统结构图
3 实验与结果分析
3.1 仿真实验与结果分析
根据前文所述方法,系统的状态方程与量测方程表示为:

(10)
Z=HXINS+VBDS.
(11)
选取INS的东、北向位置误差,东、北向速度误差,欧拉角误差,加速度计东、北、天向零偏,陀螺仪东、北、天向漂移作为状态变量,即:
XINS=[δxδyδVxδVyδψδθx
(12)
系统矩阵与初始参数详见文献[3].系统噪声WINS设为均值为零,方差为预估值Q的零均值白噪声.
选择BDS与INS的位置、偏航角误差作为量测量,则量测量为:

(13)
式中,xBDS、yBDS、ψBDS分别为BDS得到的车辆在导航坐标系下的坐标位置与偏航角.量测矩阵H=[I3×3O10×10].量测噪声方差阵VBDS是方差为预估值R的零均值白噪声.
仿真中假设载体由原点向正东方向匀速行驶,初始速度为东向10 m/s,北向0 m/s,初始东向与北向的位置误差为[2 2],初始速度误差为[0.1 0.1 0.1],东北天向初始平台误差为[20" 20" 20"],加速度计常值漂移为1×10-4g,陀螺仪的随机漂移为3 deg/h.采样周期T为1 s.在0 s—600 s期间量测噪声保持预估值,在600 s —1 200 s期间将量测噪声变为预估值的5倍,同时保持其他参数不变,将对应的RTK解算状态变为2,误差d变为5,以模拟BDS信号受建筑物遮挡的情况.仿真结果如图7、图8、图9所示:

图7 x,y方向误差
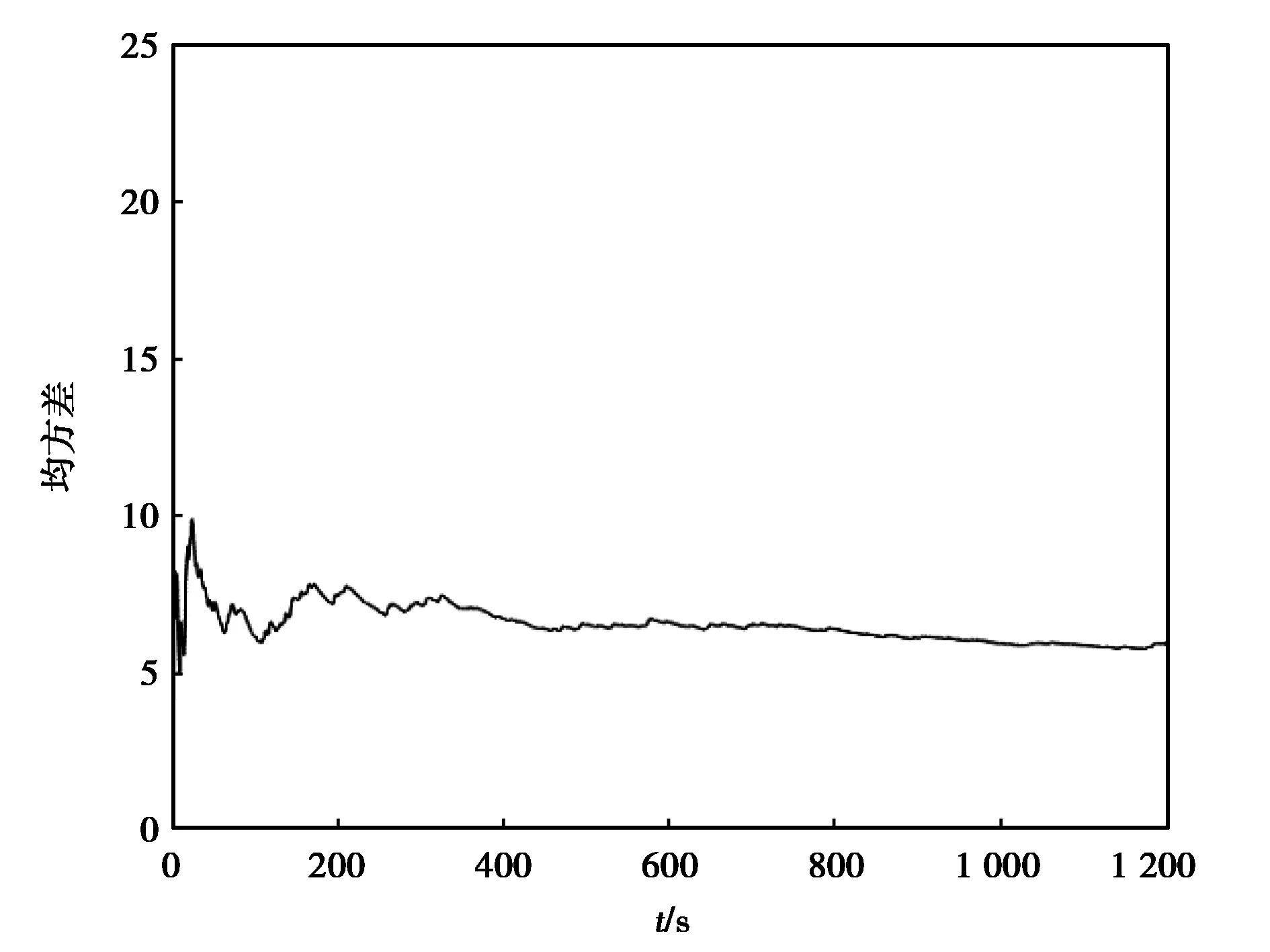
图8 x方向均方差

图9 y方向均方差
由仿真可以看出,当量测噪声保持不变时,提出的模糊Kalman滤波能很好的对车辆的运动信息进行估计.当量测噪声产生变化时,模糊Kalman滤波可以通过对系统的量测噪声方差进行调整,使得量测噪声的变化短时间内不能对滤波结果产生显著影响,系统仍保持良好的滤波精度,两个方向的均方差仍保持收敛.
3.2 实验设计与结果分析
3.2.1 实验设计
在模拟港口环境下的无人车辆上进行了数据采集.数据采集过程如下:无人车上分别搭载了北斗星通公司生产的M600双天线定位定向全球卫星导航系统(GNSS)接收机与Inertial labs公司生产的型号为IMU-P(Industrial)的惯性测量单元(IMU),负责GPS信号与加速度信号的采集.GNSS接收机的水平方向上双频RTK的定位精度为±(10+0.5×10-6×D) mm(D为定位天线之间的距离,实验中设为3 m),垂直方向上定位精度为±(10+0.5×10-6×D) mm;IMU中陀螺仪的随机漂移为3 deg/h,加速度计的常值漂移误差为1×10-4.车辆沿预定路线行驶,依次经过空旷地带、完全遮挡地带与半遮挡地带,车辆行驶路线如下图所示,依次经过A、B、C、D四个点,如图10所示:
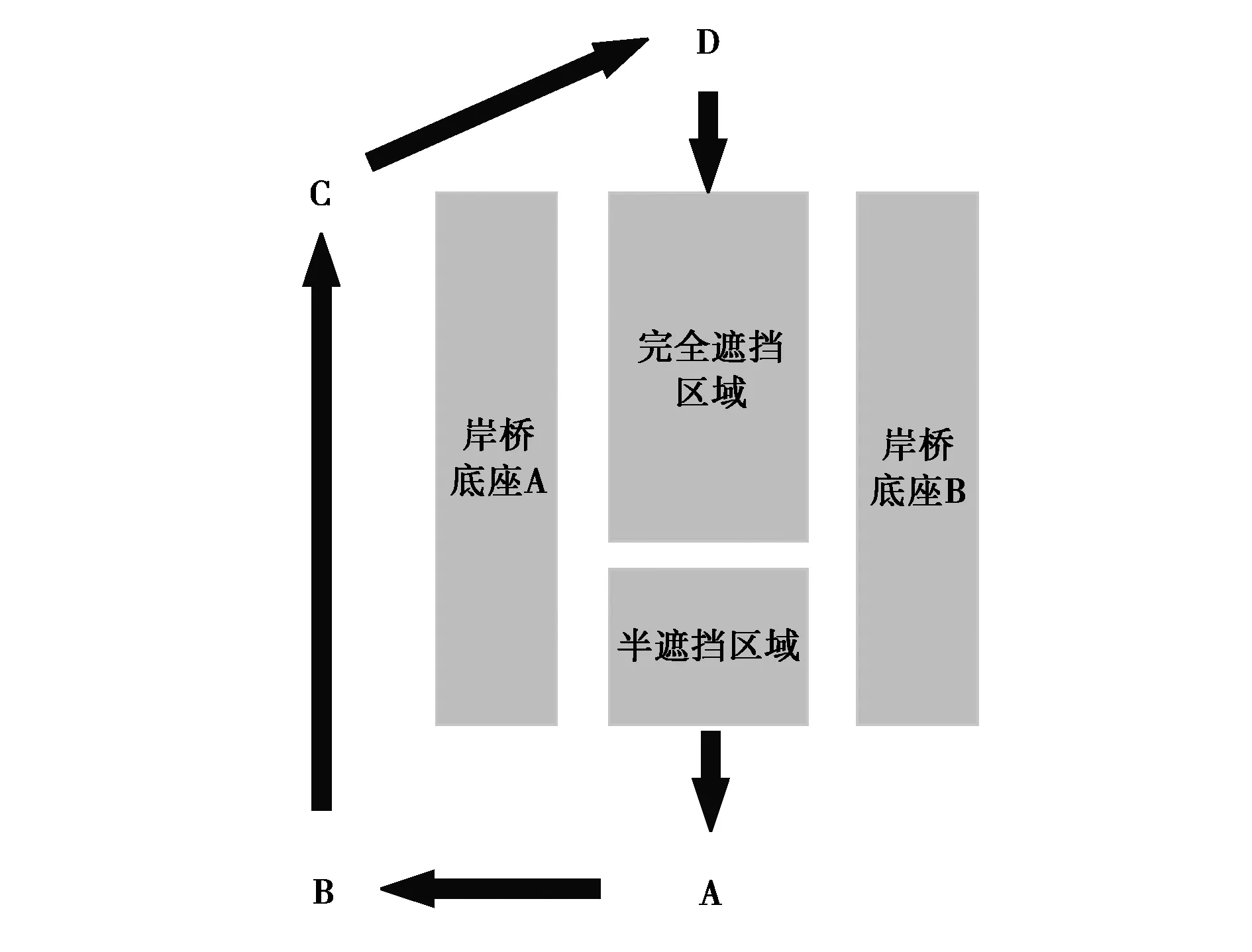
图10 车辆路线示意图
在实验中以BDS信号基站作为坐标原点,正东方向为X轴,正北方向为Y轴建立导航坐标系,在此基础上进行了多次的数据采集工作,以此为基础对提出的算法进行验证.
3.2.2 实验结果与分析
实验中,由BDS得到的车辆定位数据如图11所示.

图11 BDS定位结果
BDS在空旷地带定位结果较为理想.当车辆驶入遮挡地带、半遮挡地带(如岸桥下方、集装箱空隙之间)时,由于金属建筑物对信号的屏蔽,BDS的定位精度产生了明显的下降,且车辆运动轨迹不连续,无法满足港口内无人车辆的定位需求,需要依赖BDS/INS组合导航系统得到更为理想的定位数据.在组合导航系统中,根据建立的模型和采集的数据,分别采用传统Kalman滤波与基于传感器工作状态的模糊Kalman滤波两种滤波算法进行数据的处理,得到两种算法的滤波结果如图12所示.

图12 滤波结果对比
根据文献[7]采用的方法,以平均定位误差作为衡量定位效果优劣的指标,分别将两种方法所得到的定位结果与车辆真实行驶轨迹进行比较,结果如表1所示.

表1 定位误差对比
在整个滤波过程中,提出的模糊Kalman滤波的滤波结果相较于传统Kalman滤波的结果更为平滑.空旷地带下,二者的滤波结果相似,平均定位误差相互接近.在遮挡与半遮挡的区域内,BDS信号较弱,传统Kalman滤波过度依赖BDS提供的量测信息,当车辆处于遮挡区域时,滤波结果差,平均定位误差大幅增加,增幅达102%;提出的滤波算法根据模糊逻辑控制器的输出对量测噪声进行了及时的调整,降低了在遮挡情况下BDS失效对系统定位精度的影响,由于模糊逻辑控制器的输出为非线性的,故在试验车辆进出遮挡区域之时滤波结果相对于车辆的真实轨迹有一定的偏差,但相对于传统Kalman滤波平均误差增幅较小,增幅仅为42%,同时滤波结果更接近于车辆的真实运动轨迹.
4 结 论
本文针对港口环境下无人车辆的定位需求,提出了一种基于传感器工作状态的模糊Kalman滤波算法.提出了一种基于传感器状态的模糊逻辑控制器,通过对传感器状态的分析对量测噪声方差进行实时调整,提高了无人车辆的定位精度.建立了系统的时变模型并进行了仿真,在此基础上在类港口环境下的无人车辆上进行了实验验证.实验表明,提出的算法能准确地反映车辆的运动状态,描述车辆的真实运动,并且相较于传统的Kalman滤波有着更好的鲁棒性,在BDS信号受到干扰的情况下仍保持较高的定位精度,同时该系统易于实现,能有效解决港口环境下无人车辆的定位问题.

